高中数学苏教版(2022春 )选择性必修第二册 6.2.2 第2课时 空间向量数量积的坐标运算及空间两点间的距离公式(课件80张PPT)
文档属性
| 名称 | 高中数学苏教版(2022春 )选择性必修第二册 6.2.2 第2课时 空间向量数量积的坐标运算及空间两点间的距离公式(课件80张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 00:00:00 | ||
图片预览








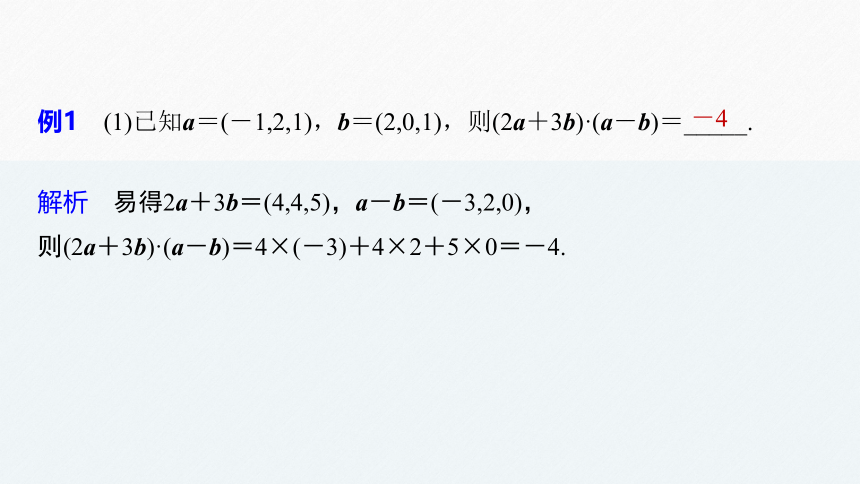



文档简介
(共80张PPT)
第2课时 空间向量数量积的坐标运算及空间两点间的距离公式
第6章 6.2.2 空间向量的坐标表示
1.会用坐标法计算空间向量的数量积,会判断空间向量的垂直,
会求空间两向量的夹角.
2.理解空间两点间距离公式的推导方法.
3.掌握空间两点间的距离公式及简单应用.
学习目标
对于平面内两个非零向量a=(x1,y1)和b=(x2,y2),有a·b=x1x2+y1y2.那么,对于空间两个非零向量,它们的数量积的坐标表示又是怎样的呢?
导语
随堂演练
课时对点练
一、空间向量数量积、垂直及模、夹角的坐标表示
二、空间两点间的距离公式及线段的中点坐标
三、利用向量的坐标运算解决平行、垂直问题
内容索引
一、空间向量数量积、垂直及模、夹角的坐标表示
问题1 设空间两个非零向量为a=(x1,y1,z1),b=(x2,y2,z2),a·b=x1x2+y1y2+z1z2成立吗?该计算公式如何推导?
提示 a·b=x1x2+y1y2+z1z2成立,证明推导过程如下:
设{i,j,k}为空间的一个单位正交基底,则
a=(x1,y1,z1)=x1i+y1j+z1k,
b=(x2,y2,z2)=x2i+y2j+z2k.
a·b=(x1i+y1j+z1k)·(x2i+y2j+z2k)
=x1x2i2+y1y2j2+z1z2k2+x1y2i·j+x1z2i·k+y1x2j·i+y1z2j·k+z1x2k·i+z1y2k·j
=x1x2+y1y2+z1z2.
名称 满足条件 向量表示形式 坐标表示形式
a·b |a||b|cos〈a,b〉 _______________
a⊥b a·b=0 __________________
模 ____________
夹角余弦
知识梳理
设a=(x1,y1,z1),b=(x2,y2,z2),则
x1x2+y1y2+z1z2
x1x2+y1y2+z1z2=0
注意点:
(1)数量积的结果为数量.
(2)两个向量的数量积等于它们对应坐标的乘积的和.
例1 (1)已知a=(-1,2,1),b=(2,0,1),则(2a+3b)·(a-b)=_____.
-4
解析 易得2a+3b=(4,4,5),a-b=(-3,2,0),
则(2a+3b)·(a-b)=4×(-3)+4×2+5×0=-4.
①求证:EF⊥B1C;
证明 如图,建立空间直角坐标系D-xyz,D为坐标原点,
反思感悟 关于空间向量坐标运算的两类问题
(1)直接计算问题
首先将空间向量用坐标表示出来,然后准确运用空间向量坐标运算公式计算.
(2)由条件求向量或点的坐标
首先把向量用坐标形式设出来,然后通过建立方程(组),解方程(组)求出其坐标.
跟踪训练1 已知向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),a∥b,b⊥c.
(1)求x,y,z的值;
解 ∵a=(x,1,2),b=(1,y,-2),c=(3,1,z),
且a∥b,b⊥c,
(2)求向量(a+c)与(b+c)所成角的余弦值.
解 由(1)知a=(-1,1,2),b=(1,-1,-2),c=(3,1,1),
∴a+c=(2,2,3),b+c=(4,0,-1).
∴(a+c)·(b+c)=2×4+2×0+3×(-1)=5,
二、空间两点间的距离公式及线段的中点坐标
问题2 你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
提示 如图,建立空间直角坐标系O-xyz,
问题3 如何用向量的方法推导出线段AB的中点坐标公式?
在空间直角坐标系中,设A(x1,y1,z1),B(x2,y2,z2),则
(1)AB= =_____________________________.
(2)线段AB的中点M的坐标为_______________________.
知识梳理
注意点:
(1)空间两点间的距离公式类似于平面中的两点之间的距离公式,可以类比记忆.
(2)空间两点间距离公式是平面两点间距离公式的推广.动点P(x,y,z)到定点P0(x0,y0,z0)的距离等于定长r(r>0)的轨迹方程为(x-x0)2+(y-y0)2+(z-z0)2=r2,此方程表示以点P0为球心,以r为半径的球面.
例2 如图所示,正方体的棱长为1,以正方体的同一顶点上的三条棱所在的直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的体对角线AB上,点Q在正方体的棱CD上.当点P为体对角线AB的中点,点Q在棱CD上运动时,求PQ的最小值.
设点Q(0,1,z)(0≤z≤1),则
反思感悟 利用空间两点间的距离公式求线段长度问题的一般步骤
跟踪训练2 已知点M(3,2,1),N(1,0,5),求:
(1)线段MN的长度;
解 根据空间两点间的距离公式得线段MN的长度
(2)到M,N两点的距离相等的点P(x,y,z)的坐标满足的条件.
解 因为点P(x,y,z)到M,N两点的距离相等.
所以有下面等式成立:
化简得x+y-2z+3=0,
因此,到M,N两点的距离相等的点P(x,y,z)的坐标满足的条件是x+y-2z+3=0.
三、利用向量的坐标运算解决平行、垂直问题
由题意,可设点P的坐标为(a,a,1),
所以3(a-1,a-1,0)=(-a,-a,0),
由题意可设点Q的坐标为(b,b,0),
延伸探究
1.若本例中的“PQ⊥AE”改为“B1Q⊥EQ”,其他条件不变,结果如何?
4c2-4c+1=0,
所以点Q是线段BD的中点,
2.本例中若G是A1D的中点,点H在平面AC上,且GH∥BD1,试判断点H的位置.
反思感悟 (1)判断两向量是否平行或垂直可直接利用向量平行或垂直的充要条件;已知两向量平行或垂直求参数值,则利用平行、垂直的充要条件,将位置关系转化为坐标关系,列方程(组)求解.
(2)利用向量证明直线、平面平行或垂直,则要建立恰当的空间直角坐标系,求出相关向量的坐标,利用向量平行、垂直的充要条件证明.
跟踪训练3 已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),若直线OA上的一点H满足BH⊥OA,则点H的坐标为_____________.
因为BH⊥OA,
即-x+y-1=0, ①
又点H在直线OA上,
1.知识清单:
(1)空间向量数量积、垂直及模、夹角的坐标表示.
(2)空间两点间的距离公式及线段的中点坐标公式.
(3)利用向量的坐标运算解决平行、垂直问题.
2.方法归纳:坐标法.
3.常见误区:
(1)把两直线的夹角混淆为两个向量的夹角,导致出错.
(2)混淆空间向量平行与垂直的条件.
课堂小结
随堂演练
1.若向量a=(4,2,-4),b=(6,-3,2),则(2a-3b)·(a+2b)等于
A.-212 B.-106 C.106 D.212
1
2
3
4
√
解析 (2a-3b)·(a+2b)
=(-10,13,-14)·(16,-4,0)
=-10×16+13×(-4)=-212.
1
2
3
4
√
1
2
3
4
3.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是
√
解析 依题意得(ka+b)·(2a-b)=0,
所以2k|a|2-ka·b+2a·b-|b|2=0,
而|a|2=2,|b|2=5,a·b=-1,
1
2
3
4
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离CM的值为
16
√
2.已知向量a=(0,-1,1),b=(4,1,0),|λa+b|= ,且λ>0,则λ等于
A.5 B.4 C.3 D.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
√
且λ>0,解得λ=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.30° B.60° C.120° D.150°
解析 a+b=(-1,-2,-3)=-a,
故(a+b)·c=-a·c=7,
得a·c=-7,
√
所以〈a,c〉=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴BC⊥AC,
所以△ABC是直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使PQ=18,则Q点的坐标为
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
所以λ=2,
所以(x0-1,y0-2,z0-3)=2(-4,-1,8),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知向量a=(1,1,-1),b=(2,-1,0),c=(0,1,-2),则下列结论正确的是
A.a·(b+c)=4
B.(a-b)·(b-c)=-8
C.记a与b-c的夹角为θ,则cos θ=
D.若(a+λb)⊥c,则λ=3
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得a·(b+c)=(1,1,-1)·(2,0,-2)=2+0+2=4,(a-b)·(b-c)=(-1,2,-1)·(2,-2,2)=-2-4-2=-8.
因为(a+λb)⊥c,所以(a+λb)·c=0,
即(1+2λ,1-λ,-1)·(0,1,-2)=0,
得1-λ+2=0,解得λ=3.
综上可知,选项ABD正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知a=(1,1,0),b=(0,1,1),c=(1,0,1),p=a-b,q=a+2b-c,则p·q=_____.
-1
解析 ∵p=a-b=(1,0,-1),
q=a+2b-c=(0,3,1),
∴p·q=1×0+0×3+(-1)×1=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知a=(cos α,1,sin α),b=(sin α,1,cos α),则向量a+b与a-b的夹角是_____.
90°
解析 ∵a=(cos α,1,sin α),b=(sin α,1,cos α),
∴a+b=(sin α+cos α,2,sin α+cos α),
a-b=(cos α-sin α,0,sin α-cos α),
∴(a+b)·(a-b)=cos2α-sin2α+sin2α-cos2α=0,
∴(a+b)⊥(a-b).
∴向量a+b与a-b的夹角是90°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知向量a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),且a∥b,b⊥c.
(1)求向量a,b,c;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x=2,y=-4,
此时a=(2,4,1),b=(-2,-4,-1).
又由b⊥c得b·c=0,
故(-2,-4,-1)·(3,-2,z)=-6+8-z=0,
得z=2,此时c=(3,-2,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求向量a+c与向量b+c所成角的余弦值.
解 由(1)得,
a+c=(5,2,3),b+c=(1,-6,1),
因此向量a+c与向量b+c所成角θ的余弦值为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求点A,B,C,P的坐标;
解 取AC的中点O,连接OB,OP.
所以AC=4,OB=2.
因为PA=PB=PC,所以点P在平面ABC上的射影是△ABC的外心,即点O.
故PO⊥平面ABC.
以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求AB,PC的中点之间的距离.
解 由(1)得AB的中点坐标为(1,-1,0),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在空间直角坐标系中,已知点P(x,y,z)的坐标满足方程(x-2)2+(y+1)2+(z-3)2=1,则点P的轨迹是
A.圆 B.直线 C.球面 D.线段
√
解析 (x-2)2+(y+1)2+(z-3)2=1表示(x,y,z)到点(2,-1,3)的距离的平方为1,它表示以(2,-1,3)为球心,以1为半径的球面,故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a与b的夹角为钝角,
所以a·b<0,
若a与b的夹角为180°,
则存在λ<0,使a=λb(λ<0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.一束光线自点P(1,1,1)出发,被xOy平面反射到达点Q(3,3,6)被吸收,那么光所走的距离是______.
解析 P关于xOy平面对称的点为P′(1,1,-1),则光线所经过的路程为
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是AA1,CB1的中点.
(1)求BM,BN的长;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 以C为原点,以CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
则B(0,1,0),M(1,0,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求△BMN的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
第2课时 空间向量数量积的坐标运算及空间两点间的距离公式
第6章 6.2.2 空间向量的坐标表示
1.会用坐标法计算空间向量的数量积,会判断空间向量的垂直,
会求空间两向量的夹角.
2.理解空间两点间距离公式的推导方法.
3.掌握空间两点间的距离公式及简单应用.
学习目标
对于平面内两个非零向量a=(x1,y1)和b=(x2,y2),有a·b=x1x2+y1y2.那么,对于空间两个非零向量,它们的数量积的坐标表示又是怎样的呢?
导语
随堂演练
课时对点练
一、空间向量数量积、垂直及模、夹角的坐标表示
二、空间两点间的距离公式及线段的中点坐标
三、利用向量的坐标运算解决平行、垂直问题
内容索引
一、空间向量数量积、垂直及模、夹角的坐标表示
问题1 设空间两个非零向量为a=(x1,y1,z1),b=(x2,y2,z2),a·b=x1x2+y1y2+z1z2成立吗?该计算公式如何推导?
提示 a·b=x1x2+y1y2+z1z2成立,证明推导过程如下:
设{i,j,k}为空间的一个单位正交基底,则
a=(x1,y1,z1)=x1i+y1j+z1k,
b=(x2,y2,z2)=x2i+y2j+z2k.
a·b=(x1i+y1j+z1k)·(x2i+y2j+z2k)
=x1x2i2+y1y2j2+z1z2k2+x1y2i·j+x1z2i·k+y1x2j·i+y1z2j·k+z1x2k·i+z1y2k·j
=x1x2+y1y2+z1z2.
名称 满足条件 向量表示形式 坐标表示形式
a·b |a||b|cos〈a,b〉 _______________
a⊥b a·b=0 __________________
模 ____________
夹角余弦
知识梳理
设a=(x1,y1,z1),b=(x2,y2,z2),则
x1x2+y1y2+z1z2
x1x2+y1y2+z1z2=0
注意点:
(1)数量积的结果为数量.
(2)两个向量的数量积等于它们对应坐标的乘积的和.
例1 (1)已知a=(-1,2,1),b=(2,0,1),则(2a+3b)·(a-b)=_____.
-4
解析 易得2a+3b=(4,4,5),a-b=(-3,2,0),
则(2a+3b)·(a-b)=4×(-3)+4×2+5×0=-4.
①求证:EF⊥B1C;
证明 如图,建立空间直角坐标系D-xyz,D为坐标原点,
反思感悟 关于空间向量坐标运算的两类问题
(1)直接计算问题
首先将空间向量用坐标表示出来,然后准确运用空间向量坐标运算公式计算.
(2)由条件求向量或点的坐标
首先把向量用坐标形式设出来,然后通过建立方程(组),解方程(组)求出其坐标.
跟踪训练1 已知向量a=(x,1,2),b=(1,y,-2),c=(3,1,z),a∥b,b⊥c.
(1)求x,y,z的值;
解 ∵a=(x,1,2),b=(1,y,-2),c=(3,1,z),
且a∥b,b⊥c,
(2)求向量(a+c)与(b+c)所成角的余弦值.
解 由(1)知a=(-1,1,2),b=(1,-1,-2),c=(3,1,1),
∴a+c=(2,2,3),b+c=(4,0,-1).
∴(a+c)·(b+c)=2×4+2×0+3×(-1)=5,
二、空间两点间的距离公式及线段的中点坐标
问题2 你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
提示 如图,建立空间直角坐标系O-xyz,
问题3 如何用向量的方法推导出线段AB的中点坐标公式?
在空间直角坐标系中,设A(x1,y1,z1),B(x2,y2,z2),则
(1)AB= =_____________________________.
(2)线段AB的中点M的坐标为_______________________.
知识梳理
注意点:
(1)空间两点间的距离公式类似于平面中的两点之间的距离公式,可以类比记忆.
(2)空间两点间距离公式是平面两点间距离公式的推广.动点P(x,y,z)到定点P0(x0,y0,z0)的距离等于定长r(r>0)的轨迹方程为(x-x0)2+(y-y0)2+(z-z0)2=r2,此方程表示以点P0为球心,以r为半径的球面.
例2 如图所示,正方体的棱长为1,以正方体的同一顶点上的三条棱所在的直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的体对角线AB上,点Q在正方体的棱CD上.当点P为体对角线AB的中点,点Q在棱CD上运动时,求PQ的最小值.
设点Q(0,1,z)(0≤z≤1),则
反思感悟 利用空间两点间的距离公式求线段长度问题的一般步骤
跟踪训练2 已知点M(3,2,1),N(1,0,5),求:
(1)线段MN的长度;
解 根据空间两点间的距离公式得线段MN的长度
(2)到M,N两点的距离相等的点P(x,y,z)的坐标满足的条件.
解 因为点P(x,y,z)到M,N两点的距离相等.
所以有下面等式成立:
化简得x+y-2z+3=0,
因此,到M,N两点的距离相等的点P(x,y,z)的坐标满足的条件是x+y-2z+3=0.
三、利用向量的坐标运算解决平行、垂直问题
由题意,可设点P的坐标为(a,a,1),
所以3(a-1,a-1,0)=(-a,-a,0),
由题意可设点Q的坐标为(b,b,0),
延伸探究
1.若本例中的“PQ⊥AE”改为“B1Q⊥EQ”,其他条件不变,结果如何?
4c2-4c+1=0,
所以点Q是线段BD的中点,
2.本例中若G是A1D的中点,点H在平面AC上,且GH∥BD1,试判断点H的位置.
反思感悟 (1)判断两向量是否平行或垂直可直接利用向量平行或垂直的充要条件;已知两向量平行或垂直求参数值,则利用平行、垂直的充要条件,将位置关系转化为坐标关系,列方程(组)求解.
(2)利用向量证明直线、平面平行或垂直,则要建立恰当的空间直角坐标系,求出相关向量的坐标,利用向量平行、垂直的充要条件证明.
跟踪训练3 已知空间三点O(0,0,0),A(-1,1,0),B(0,1,1),若直线OA上的一点H满足BH⊥OA,则点H的坐标为_____________.
因为BH⊥OA,
即-x+y-1=0, ①
又点H在直线OA上,
1.知识清单:
(1)空间向量数量积、垂直及模、夹角的坐标表示.
(2)空间两点间的距离公式及线段的中点坐标公式.
(3)利用向量的坐标运算解决平行、垂直问题.
2.方法归纳:坐标法.
3.常见误区:
(1)把两直线的夹角混淆为两个向量的夹角,导致出错.
(2)混淆空间向量平行与垂直的条件.
课堂小结
随堂演练
1.若向量a=(4,2,-4),b=(6,-3,2),则(2a-3b)·(a+2b)等于
A.-212 B.-106 C.106 D.212
1
2
3
4
√
解析 (2a-3b)·(a+2b)
=(-10,13,-14)·(16,-4,0)
=-10×16+13×(-4)=-212.
1
2
3
4
√
1
2
3
4
3.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是
√
解析 依题意得(ka+b)·(2a-b)=0,
所以2k|a|2-ka·b+2a·b-|b|2=0,
而|a|2=2,|b|2=5,a·b=-1,
1
2
3
4
课时对点练
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离CM的值为
16
√
2.已知向量a=(0,-1,1),b=(4,1,0),|λa+b|= ,且λ>0,则λ等于
A.5 B.4 C.3 D.2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 λa+b=λ(0,-1,1)+(4,1,0)=(4,1-λ,λ),
√
且λ>0,解得λ=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
A.30° B.60° C.120° D.150°
解析 a+b=(-1,-2,-3)=-a,
故(a+b)·c=-a·c=7,
得a·c=-7,
√
所以〈a,c〉=120°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.已知A(1,-2,11),B(4,2,3),C(6,-1,4),则△ABC的形状是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴BC⊥AC,
所以△ABC是直角三角形.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.从点P(1,2,3)出发,沿着向量v=(-4,-1,8)方向取点Q,使PQ=18,则Q点的坐标为
A.(-1,-2,3) B.(9,4,-13)
C.(-7,0,19) D.(1,-2,-3)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即(x0-1,y0-2,z0-3)=λ(-4,-1,8).
所以λ=2,
所以(x0-1,y0-2,z0-3)=2(-4,-1,8),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知向量a=(1,1,-1),b=(2,-1,0),c=(0,1,-2),则下列结论正确的是
A.a·(b+c)=4
B.(a-b)·(b-c)=-8
C.记a与b-c的夹角为θ,则cos θ=
D.若(a+λb)⊥c,则λ=3
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 由题意得a·(b+c)=(1,1,-1)·(2,0,-2)=2+0+2=4,(a-b)·(b-c)=(-1,2,-1)·(2,-2,2)=-2-4-2=-8.
因为(a+λb)⊥c,所以(a+λb)·c=0,
即(1+2λ,1-λ,-1)·(0,1,-2)=0,
得1-λ+2=0,解得λ=3.
综上可知,选项ABD正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.已知a=(1,1,0),b=(0,1,1),c=(1,0,1),p=a-b,q=a+2b-c,则p·q=_____.
-1
解析 ∵p=a-b=(1,0,-1),
q=a+2b-c=(0,3,1),
∴p·q=1×0+0×3+(-1)×1=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知a=(cos α,1,sin α),b=(sin α,1,cos α),则向量a+b与a-b的夹角是_____.
90°
解析 ∵a=(cos α,1,sin α),b=(sin α,1,cos α),
∴a+b=(sin α+cos α,2,sin α+cos α),
a-b=(cos α-sin α,0,sin α-cos α),
∴(a+b)·(a-b)=cos2α-sin2α+sin2α-cos2α=0,
∴(a+b)⊥(a-b).
∴向量a+b与a-b的夹角是90°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.已知向量a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),且a∥b,b⊥c.
(1)求向量a,b,c;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解得x=2,y=-4,
此时a=(2,4,1),b=(-2,-4,-1).
又由b⊥c得b·c=0,
故(-2,-4,-1)·(3,-2,z)=-6+8-z=0,
得z=2,此时c=(3,-2,2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求向量a+c与向量b+c所成角的余弦值.
解 由(1)得,
a+c=(5,2,3),b+c=(1,-6,1),
因此向量a+c与向量b+c所成角θ的余弦值为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求点A,B,C,P的坐标;
解 取AC的中点O,连接OB,OP.
所以AC=4,OB=2.
因为PA=PB=PC,所以点P在平面ABC上的射影是△ABC的外心,即点O.
故PO⊥平面ABC.
以O为坐标原点,OB,OC,OP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求AB,PC的中点之间的距离.
解 由(1)得AB的中点坐标为(1,-1,0),
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.在空间直角坐标系中,已知点P(x,y,z)的坐标满足方程(x-2)2+(y+1)2+(z-3)2=1,则点P的轨迹是
A.圆 B.直线 C.球面 D.线段
√
解析 (x-2)2+(y+1)2+(z-3)2=1表示(x,y,z)到点(2,-1,3)的距离的平方为1,它表示以(2,-1,3)为球心,以1为半径的球面,故选C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为a与b的夹角为钝角,
所以a·b<0,
若a与b的夹角为180°,
则存在λ<0,使a=λb(λ<0),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.一束光线自点P(1,1,1)出发,被xOy平面反射到达点Q(3,3,6)被吸收,那么光所走的距离是______.
解析 P关于xOy平面对称的点为P′(1,1,-1),则光线所经过的路程为
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.如图,在直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M,N分别是AA1,CB1的中点.
(1)求BM,BN的长;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解 以C为原点,以CA,CB,CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图.
则B(0,1,0),M(1,0,1),
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求△BMN的面积.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
本课结束
