2022年人教版七年级数学下册5.3.1平行线的性质 基础练习(Word版含答案)
文档属性
| 名称 | 2022年人教版七年级数学下册5.3.1平行线的性质 基础练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 436.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 23:23:27 | ||
图片预览

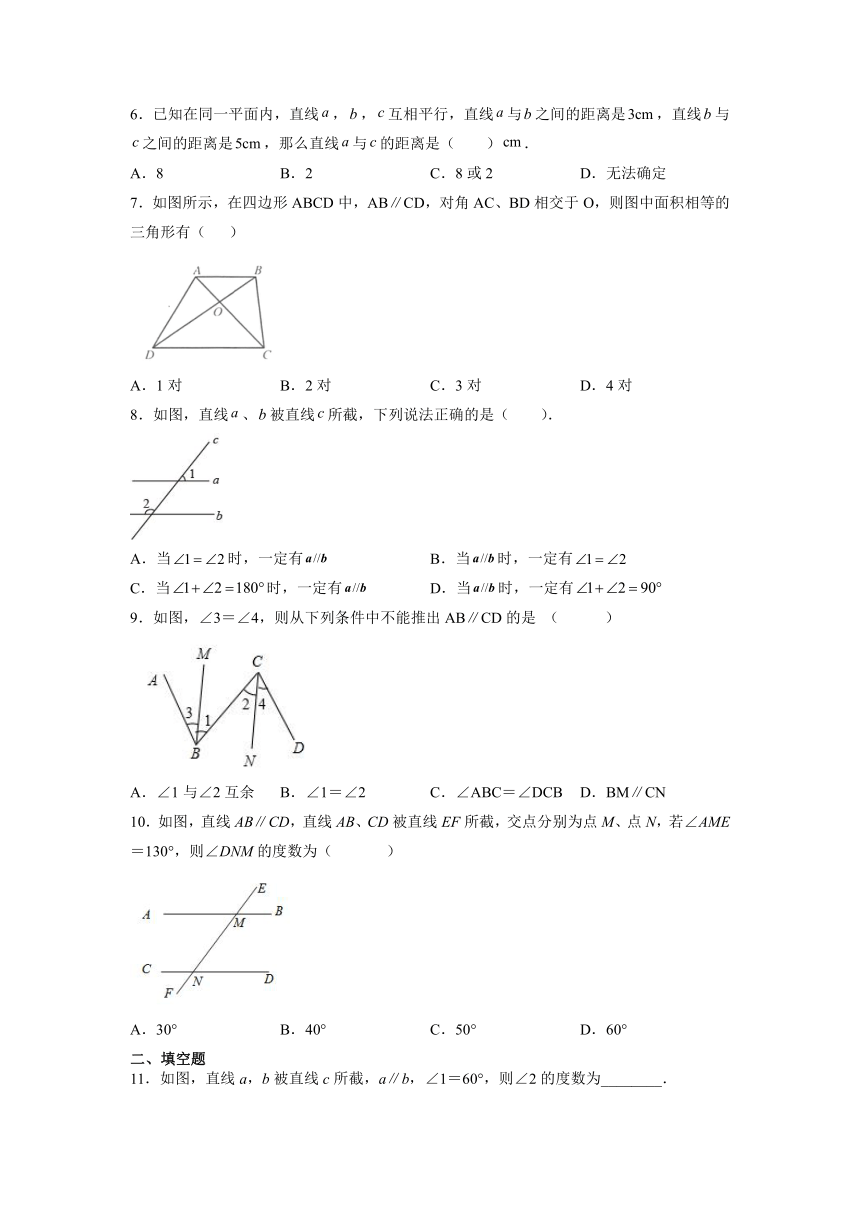
文档简介
5.3.1平行线的性质基础练习
一、单选题
1.已知直线,点在上,点,,在上,且,,,则与之间的距离为( )
A.等于 B.等于 C.等于 D.小于或等于
2.直线,直线与,分别交于点,,.若,则的度数为( )
A. B. C. D.
3.已知:如图AB//EF,BC⊥CD,则∠,∠,∠之间的关系是( )
A. B.
C. D.
4.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
5.如图,若AB∥CD,CD∥EF,那么BCE=( )
A.180°-2+1 B.180°-1-2 C.2=21 D.1+2
6.已知在同一平面内,直线,,互相平行,直线与之间的距离是,直线与之间的距离是,那么直线与的距离是( ).
A.8 B.2 C.8或2 D.无法确定
7.如图所示,在四边形ABCD中,AB∥CD,对角AC、BD相交于O,则图中面积相等的三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,直线、被直线所截,下列说法正确的是( ).
A.当时,一定有 B.当时,一定有
C.当时,一定有 D.当时,一定有
9.如图,∠3=∠4,则从下列条件中不能推出AB∥CD的是 ( )
A.∠1与∠2互余 B.∠1=∠2 C.∠ABC=∠DCB D.BM∥CN
10.如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
11.如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为________.
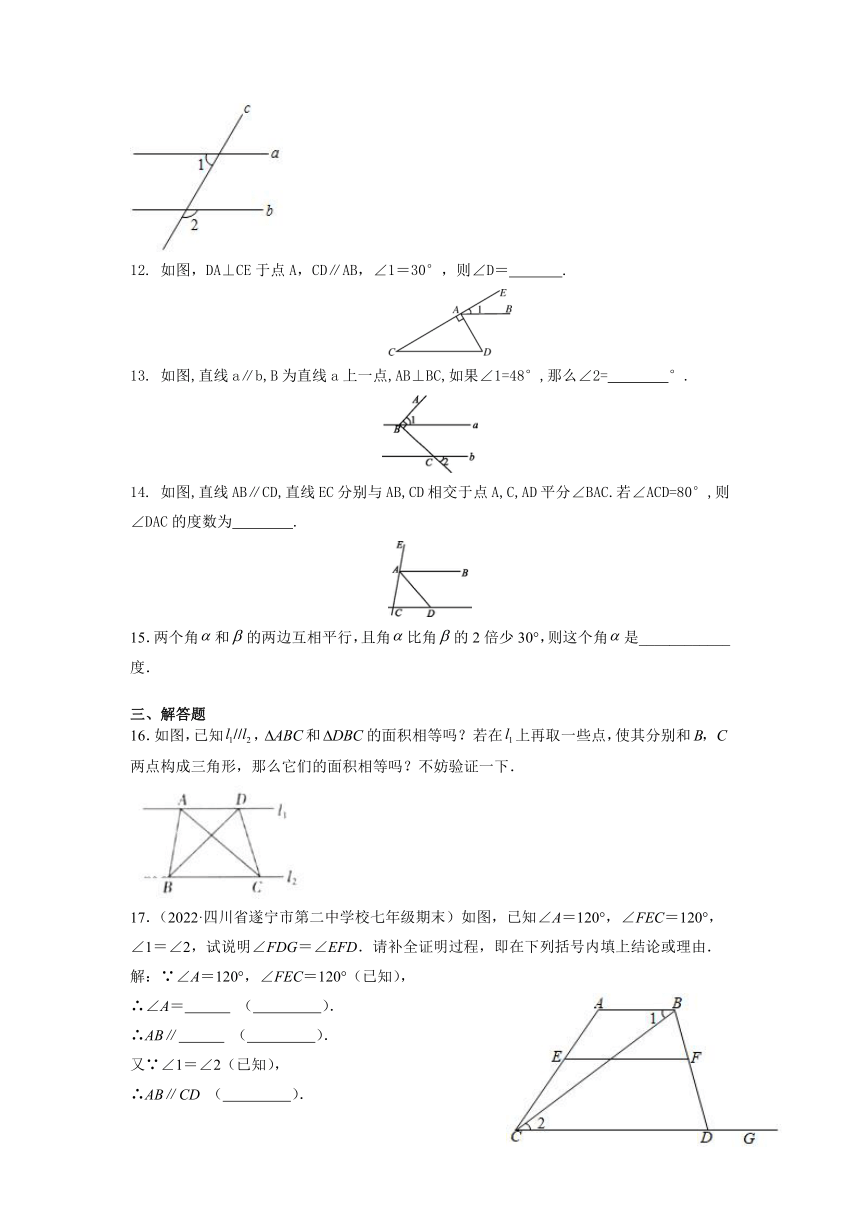
12. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
13. 如图,直线a∥b,B为直线a上一点,AB⊥BC,如果∠1=48°,那么∠2= °.
14. 如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC.若∠ACD=80°,则∠DAC的度数为 .
15.两个角和的两边互相平行,且角比角的2倍少30°,则这个角是____________度.
三、解答题
16.如图,已知,和的面积相等吗?若在上再取一些点,使其分别和两点构成三角形,那么它们的面积相等吗?不妨验证一下.
17.(2022·四川省遂宁市第二中学校七年级期末)如图,已知∠A=120°,∠FEC=120°,∠1=∠2,试说明∠FDG=∠EFD.请补全证明过程,即在下列括号内填上结论或理由.
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A= ( ).
∴AB∥ ( ).
又∵∠1=∠2(已知),
∴AB∥CD ( ).
∴EF∥ ( ).
∴∠FDG=∠EFD ( ).
18.(2022·吉林·长春外国语学校七年级期末)阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FGCD,∠1 = ∠3.
求证:∠B + ∠BDE= 180°.
解:因为FGCD(已知),
所以∠1= .
又因为∠1 = ∠3 (已知),
所以∠2 = (等量代换).
所以BC ( ),
所以∠B + ∠BDE = 180°(___________________).
19.(2021·河南灵宝·七年级期中)如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
20.(2021·贵州碧江·七年级期末)如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
参考答案
1.D 2.B 3.C 4.A 5.A 6.C 7.C 8.C 9.A 10.C
11.120°
12. 60°
13. 42
14. 50°
15.或
16.解: 和面积相等.
验证;如图,过点作于点,过点作于点.
则根据平行线间的距离相等,得.
因为,,
两个三角形同底等高,所以面积相等.
若在上再取一些点,使其分别和两点构成三角形,那么它们的面积相等.
如图,在上取异于两点的点,过点作于点,则.
和是同底等高,所以面积相等.
17.【详解】
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A=∠FEC(等量代换),
∴AB∥EF(同位角相等,两直线平行),
又∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
∴EF∥CD(平行于同一条直线的两直线互相平行),
∴∠FDG=∠EFD(两直线平行,内错角相等),
故答案为:∠FEC;等量代换;EF;同位角相等,两直线平行;内错角相等,两直线平行;CD;平行于同一条直线的两直线互相平行;两直线平行,内错角相等.
18.【详解】
解:因为FGCD(已知),
所以∠1=∠2.
又因为∠1 = ∠3 (已知),
所以∠2 =∠3(等量代换).
所以(内错角相等,两直线平行),
所以∠B + ∠BDE = 180°(两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
19.【详解】
要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
20.【详解】
证明:如图,设BC与AE、GF分别交于点M、N.
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
一、单选题
1.已知直线,点在上,点,,在上,且,,,则与之间的距离为( )
A.等于 B.等于 C.等于 D.小于或等于
2.直线,直线与,分别交于点,,.若,则的度数为( )
A. B. C. D.
3.已知:如图AB//EF,BC⊥CD,则∠,∠,∠之间的关系是( )
A. B.
C. D.
4.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
5.如图,若AB∥CD,CD∥EF,那么BCE=( )
A.180°-2+1 B.180°-1-2 C.2=21 D.1+2
6.已知在同一平面内,直线,,互相平行,直线与之间的距离是,直线与之间的距离是,那么直线与的距离是( ).
A.8 B.2 C.8或2 D.无法确定
7.如图所示,在四边形ABCD中,AB∥CD,对角AC、BD相交于O,则图中面积相等的三角形有( )
A.1对 B.2对 C.3对 D.4对
8.如图,直线、被直线所截,下列说法正确的是( ).
A.当时,一定有 B.当时,一定有
C.当时,一定有 D.当时,一定有
9.如图,∠3=∠4,则从下列条件中不能推出AB∥CD的是 ( )
A.∠1与∠2互余 B.∠1=∠2 C.∠ABC=∠DCB D.BM∥CN
10.如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( )
A.30° B.40° C.50° D.60°
二、填空题
11.如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为________.
12. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
13. 如图,直线a∥b,B为直线a上一点,AB⊥BC,如果∠1=48°,那么∠2= °.
14. 如图,直线AB∥CD,直线EC分别与AB,CD相交于点A,C,AD平分∠BAC.若∠ACD=80°,则∠DAC的度数为 .
15.两个角和的两边互相平行,且角比角的2倍少30°,则这个角是____________度.
三、解答题
16.如图,已知,和的面积相等吗?若在上再取一些点,使其分别和两点构成三角形,那么它们的面积相等吗?不妨验证一下.
17.(2022·四川省遂宁市第二中学校七年级期末)如图,已知∠A=120°,∠FEC=120°,∠1=∠2,试说明∠FDG=∠EFD.请补全证明过程,即在下列括号内填上结论或理由.
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A= ( ).
∴AB∥ ( ).
又∵∠1=∠2(已知),
∴AB∥CD ( ).
∴EF∥ ( ).
∴∠FDG=∠EFD ( ).
18.(2022·吉林·长春外国语学校七年级期末)阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FGCD,∠1 = ∠3.
求证:∠B + ∠BDE= 180°.
解:因为FGCD(已知),
所以∠1= .
又因为∠1 = ∠3 (已知),
所以∠2 = (等量代换).
所以BC ( ),
所以∠B + ∠BDE = 180°(___________________).
19.(2021·河南灵宝·七年级期中)如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
20.(2021·贵州碧江·七年级期末)如图,AE⊥BC,FG⊥BC,∠1=∠2,求证:AB∥CD.
参考答案
1.D 2.B 3.C 4.A 5.A 6.C 7.C 8.C 9.A 10.C
11.120°
12. 60°
13. 42
14. 50°
15.或
16.解: 和面积相等.
验证;如图,过点作于点,过点作于点.
则根据平行线间的距离相等,得.
因为,,
两个三角形同底等高,所以面积相等.
若在上再取一些点,使其分别和两点构成三角形,那么它们的面积相等.
如图,在上取异于两点的点,过点作于点,则.
和是同底等高,所以面积相等.
17.【详解】
解:∵∠A=120°,∠FEC=120°(已知),
∴∠A=∠FEC(等量代换),
∴AB∥EF(同位角相等,两直线平行),
又∵∠1=∠2(已知),
∴AB∥CD(内错角相等,两直线平行),
∴EF∥CD(平行于同一条直线的两直线互相平行),
∴∠FDG=∠EFD(两直线平行,内错角相等),
故答案为:∠FEC;等量代换;EF;同位角相等,两直线平行;内错角相等,两直线平行;CD;平行于同一条直线的两直线互相平行;两直线平行,内错角相等.
18.【详解】
解:因为FGCD(已知),
所以∠1=∠2.
又因为∠1 = ∠3 (已知),
所以∠2 =∠3(等量代换).
所以(内错角相等,两直线平行),
所以∠B + ∠BDE = 180°(两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
19.【详解】
要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
20.【详解】
证明:如图,设BC与AE、GF分别交于点M、N.
∵AE⊥BC,FG⊥BC,
∴∠AMB=∠GNB=90°,
∴AE∥FG,
∴∠A=∠1;
又∵∠2=∠1,
∴∠A=∠2,
∴AB∥CD.
