2022年人教版七年级数学下册5.3.1平行线的性质 课后练习(word,含答案)
文档属性
| 名称 | 2022年人教版七年级数学下册5.3.1平行线的性质 课后练习(word,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 22:46:40 | ||
图片预览


文档简介
5.3.1平行线的性质
一、选择题
1.一副含30°,45°角的直角三角板按如图所示放置,已知DE//BC,则∠ABE的度数为( )
A.10° B.15° C.20° D.25°
2. 如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
3. 已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
4. 如图,直线a∥b,将一块含30°角(∠BAC=30°)的三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为 ( )
A.20° B.30° C.40° D.50°
5.如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6.一副直角三角板如图放置,其中∠F=∠ACB=90°,∠D=45°,∠B=60°,AB//DC,则∠CAE的度数为( )
A.25° B.20° C.15° D.10°
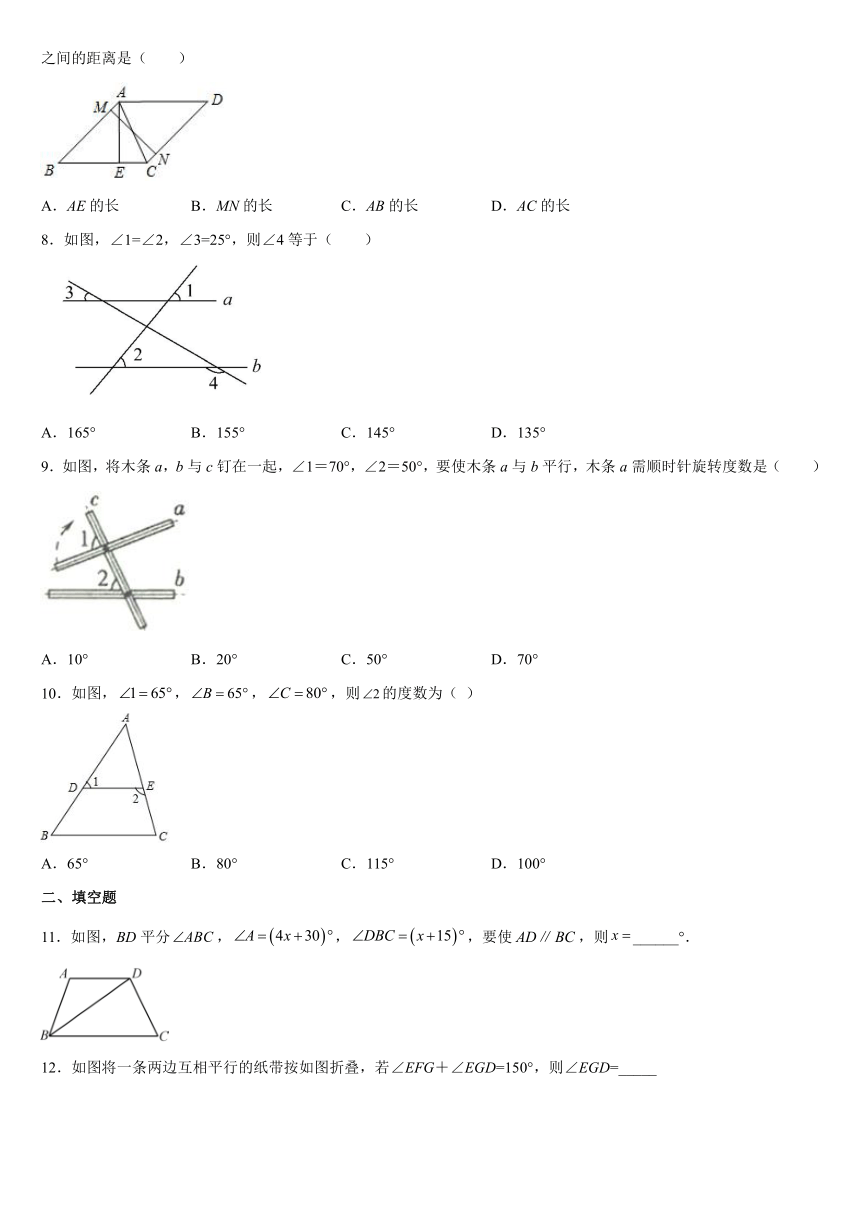
7.如图,四边形ABCD是平行四边形,点M在边AB上,AE⊥BC,MN⊥CD,垂足分别为E、N,则平行线AD与BC之间的距离是( )
A.AE的长 B.MN的长 C.AB的长 D.AC的长
8.如图,∠1=∠2,∠3=25°,则∠4等于( )
A.165° B.155° C.145° D.135°
9.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a需顺时针旋转度数是( )
A.10° B.20° C.50° D.70°
10.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
二、填空题
11.如图,BD平分,,,要使,则______°.
12.如图将一条两边互相平行的纸带按如图折叠,若∠EFG+∠EGD=150°,则∠EGD=_____
13.如图,AB∥CD,∠EGB=50°,则∠CHG的大小为 _____.
14.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=40°,则∠AEC=_____度.
15.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有______.(填序号)
三、解答题
16.如图,F是上一点,于点是上一点,于点,求证:.
17.如图,已知EFAB,∠DEF=∠A.
(1)求证:DEAC;
(2)若CD平分∠ACB,∠BED=60°,求∠ACD的度数.
18.请你补全证明过程或推理依据:
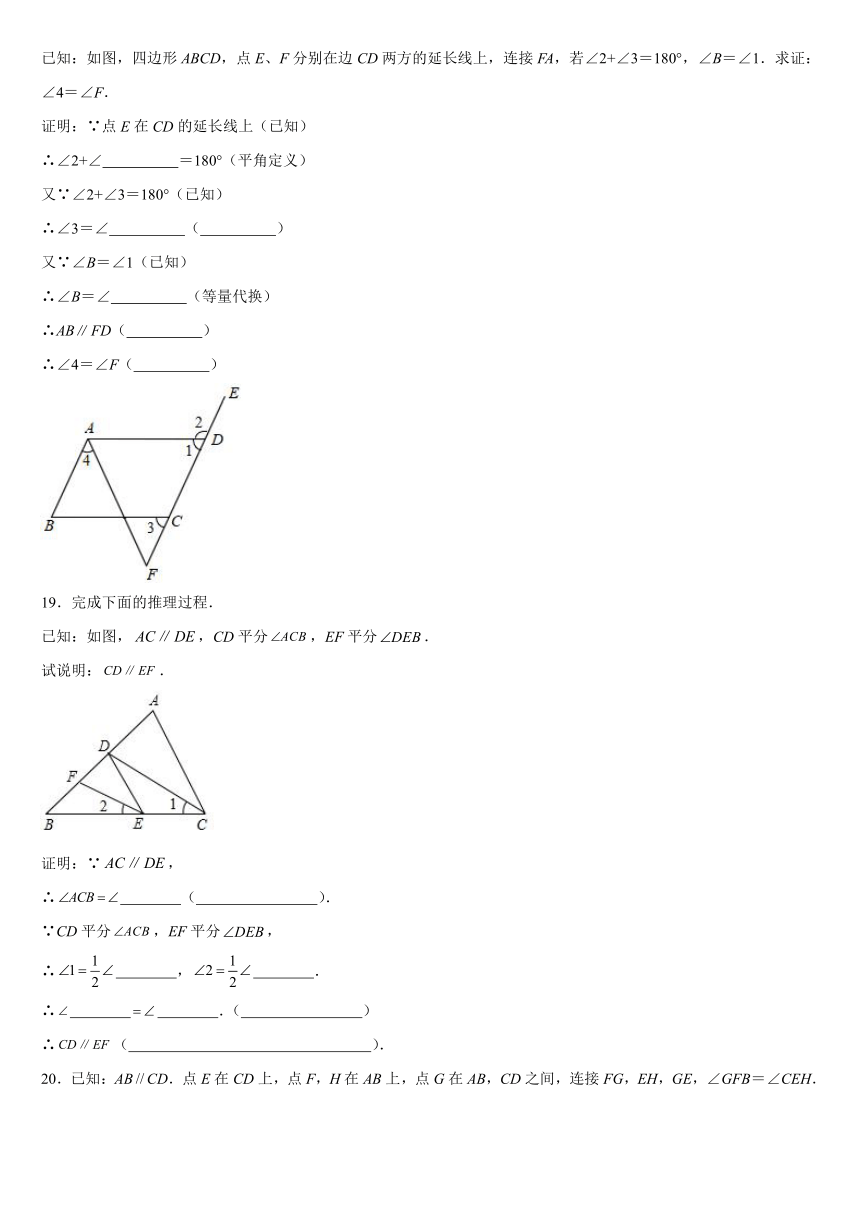
已知:如图,四边形ABCD,点E、F分别在边CD两方的延长线上,连接FA,若∠2+∠3=180°,∠B=∠1.求证:∠4=∠F.
证明:∵点E在CD的延长线上(已知)
∴∠2+∠ =180°(平角定义)
又∵∠2+∠3=180°(已知)
∴∠3=∠ ( )
又∵∠B=∠1(已知)
∴∠B=∠ (等量代换)
∴ABFD( )
∴∠4=∠F( )
19.完成下面的推理过程.
已知:如图,,CD平分,EF平分.
试说明:.
证明:∵,
∴ ( ).
∵CD平分,EF平分,
∴ , .
∴ .( )
∴( ).
20.已知:ABCD.点E在CD上,点F,H在AB上,点G在AB,CD之间,连接FG,EH,GE,∠GFB=∠CEH.
(1)如图1,求证:GFEH;
(2)如图2,若∠GEH=α,FM平分∠AFG,EM平分∠GEC,试问∠M与α之间有怎样的数量关系(用含α的式子表示∠M)?请写出你的猜想,并加以证明.
21.(2021·全国·七年级专题练习)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
22.(2019·广西港南·七年级期末)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.如图,已知AB//CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 .
(2)当△PMN所放位置如图②所示时,请猜想∠PFD与∠AEM的数量关系并证明.
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=20°,∠PEB=15°,求∠N的度数.
【参考答案】
1.B 2.D 3.D 4.C 5.A 6.C 7.A 8.B 9.B 10.D
11.20
12.
13.130°
14.70
15.①②③
16.证明:∵
∴
∵
∴
∴
∴
∴
又∵
∴,即
∴
17.(1)∵EFAB,
∴∠BDE=∠DEF,
又∠DEF=∠A
∴∠BDE=∠A,
∴DEAC;
(2)
DEAC,∠BED=60°,
CD平分∠ACB,
18.解:证明:∵点E在CD的延长线上(已知),
∴∠2+∠1=180°(平角定义).
又∵∠2+∠3=180°(已知),
∴∠3=∠1(同角的补角相等).
又∵∠B=∠1(已知),
∴∠B=∠3(等量代换).
∴AB∥FD(内错角相等,两直线平行).
∴∠4=∠F(两直线平行,内错角相等).
19.证明:∵AC∥DE,
∴∠ACB=∠DEB(两直线平行,同位角相等),
∵CD平分∠ACB,EF平分∠DEB,
∴,,
∴∠1=∠2,(等量代换)
∴CD∥EF(同位角相等,两直线平行).
故答案为:DEB;两直线平行,同位角相等;ACB;DEB;1;2;等量代换;同位角相等,两直线平行.
20.(1)证明:,
,
,
,
;
(2)解:,理由如下:
如图2,过点作,过点作,
,
,
,,
,
同理,,
平分,平分,
,,
,
由(1)知,,
,
,
,
,
.
21.【详解】
解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
22.【详解】
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
23.解:(1)如图①,
作PH//AB,则∠AEM=∠HPM,
∵AB//CD,PH//AB,
∴PH//CD,
∴∠PFD=∠HPN,
∵∠MPN=90°,
∴∠PFD+∠AEM=90°,
故答案为:∠PFD+∠AEM=90°;
(2)猜想:∠PFD﹣∠AEM=90°;
理由如下:∵AB∥CD,
∴∠PFD+∠BHN=180°,
∵∠BHN=∠PHE,
∴∠PFD+∠PHE=180°,
∵∠P=90°,
∴∠PHE+∠PEB=90°,
∵∠PEB=∠AEM,
∴∠PHE+∠AEM=90°,
∴∠PFD﹣∠AEM=90°;
(3)如图②,∵∠P=90°,∠PEB=15°,
∴∠PHE=∠P﹣∠PEB=90°﹣15°=75°,
∴∠BHF=∠PHE=75°,
∵AB//CD,
∴∠DFH+∠BHF=180°,
∴∠DFH=180°﹣∠BHF=105°,
∴∠OFN=∠DFH=105°,
∵∠DON=20°,
∴∠N=180°﹣∠DON﹣∠OFN=55°.
一、选择题
1.一副含30°,45°角的直角三角板按如图所示放置,已知DE//BC,则∠ABE的度数为( )
A.10° B.15° C.20° D.25°
2. 如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
3. 已知∠1与∠2是同旁内角.若∠1=50°,则∠2的度数是( )
A.50° B.130° C.50°或130° D.不能确定
4. 如图,直线a∥b,将一块含30°角(∠BAC=30°)的三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为 ( )
A.20° B.30° C.40° D.50°
5.如图:AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①OF平分∠BOD;②∠POE=∠BOF;③∠BOE=70°;④∠POB=2∠DOF,其中结论正确的序号是( )
A.①②③ B.①②④ C.①③④ D.①②③④
6.一副直角三角板如图放置,其中∠F=∠ACB=90°,∠D=45°,∠B=60°,AB//DC,则∠CAE的度数为( )
A.25° B.20° C.15° D.10°
7.如图,四边形ABCD是平行四边形,点M在边AB上,AE⊥BC,MN⊥CD,垂足分别为E、N,则平行线AD与BC之间的距离是( )
A.AE的长 B.MN的长 C.AB的长 D.AC的长
8.如图,∠1=∠2,∠3=25°,则∠4等于( )
A.165° B.155° C.145° D.135°
9.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a需顺时针旋转度数是( )
A.10° B.20° C.50° D.70°
10.如图,,,,则的度数为( )
A.65° B.80° C.115° D.100°
二、填空题
11.如图,BD平分,,,要使,则______°.
12.如图将一条两边互相平行的纸带按如图折叠,若∠EFG+∠EGD=150°,则∠EGD=_____
13.如图,AB∥CD,∠EGB=50°,则∠CHG的大小为 _____.
14.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=40°,则∠AEC=_____度.
15.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠1=∠2;④∠POB=2∠3.其中正确的结论有______.(填序号)
三、解答题
16.如图,F是上一点,于点是上一点,于点,求证:.
17.如图,已知EFAB,∠DEF=∠A.
(1)求证:DEAC;
(2)若CD平分∠ACB,∠BED=60°,求∠ACD的度数.
18.请你补全证明过程或推理依据:
已知:如图,四边形ABCD,点E、F分别在边CD两方的延长线上,连接FA,若∠2+∠3=180°,∠B=∠1.求证:∠4=∠F.
证明:∵点E在CD的延长线上(已知)
∴∠2+∠ =180°(平角定义)
又∵∠2+∠3=180°(已知)
∴∠3=∠ ( )
又∵∠B=∠1(已知)
∴∠B=∠ (等量代换)
∴ABFD( )
∴∠4=∠F( )
19.完成下面的推理过程.
已知:如图,,CD平分,EF平分.
试说明:.
证明:∵,
∴ ( ).
∵CD平分,EF平分,
∴ , .
∴ .( )
∴( ).
20.已知:ABCD.点E在CD上,点F,H在AB上,点G在AB,CD之间,连接FG,EH,GE,∠GFB=∠CEH.
(1)如图1,求证:GFEH;
(2)如图2,若∠GEH=α,FM平分∠AFG,EM平分∠GEC,试问∠M与α之间有怎样的数量关系(用含α的式子表示∠M)?请写出你的猜想,并加以证明.
21.(2021·全国·七年级专题练习)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
22.(2019·广西港南·七年级期末)已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
23.如图,已知AB//CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F.
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 .
(2)当△PMN所放位置如图②所示时,请猜想∠PFD与∠AEM的数量关系并证明.
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=20°,∠PEB=15°,求∠N的度数.
【参考答案】
1.B 2.D 3.D 4.C 5.A 6.C 7.A 8.B 9.B 10.D
11.20
12.
13.130°
14.70
15.①②③
16.证明:∵
∴
∵
∴
∴
∴
∴
又∵
∴,即
∴
17.(1)∵EFAB,
∴∠BDE=∠DEF,
又∠DEF=∠A
∴∠BDE=∠A,
∴DEAC;
(2)
DEAC,∠BED=60°,
CD平分∠ACB,
18.解:证明:∵点E在CD的延长线上(已知),
∴∠2+∠1=180°(平角定义).
又∵∠2+∠3=180°(已知),
∴∠3=∠1(同角的补角相等).
又∵∠B=∠1(已知),
∴∠B=∠3(等量代换).
∴AB∥FD(内错角相等,两直线平行).
∴∠4=∠F(两直线平行,内错角相等).
19.证明:∵AC∥DE,
∴∠ACB=∠DEB(两直线平行,同位角相等),
∵CD平分∠ACB,EF平分∠DEB,
∴,,
∴∠1=∠2,(等量代换)
∴CD∥EF(同位角相等,两直线平行).
故答案为:DEB;两直线平行,同位角相等;ACB;DEB;1;2;等量代换;同位角相等,两直线平行.
20.(1)证明:,
,
,
,
;
(2)解:,理由如下:
如图2,过点作,过点作,
,
,
,,
,
同理,,
平分,平分,
,,
,
由(1)知,,
,
,
,
,
.
21.【详解】
解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
22.【详解】
(1)如图1,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)不成立
如图2,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
如图3,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
23.解:(1)如图①,
作PH//AB,则∠AEM=∠HPM,
∵AB//CD,PH//AB,
∴PH//CD,
∴∠PFD=∠HPN,
∵∠MPN=90°,
∴∠PFD+∠AEM=90°,
故答案为:∠PFD+∠AEM=90°;
(2)猜想:∠PFD﹣∠AEM=90°;
理由如下:∵AB∥CD,
∴∠PFD+∠BHN=180°,
∵∠BHN=∠PHE,
∴∠PFD+∠PHE=180°,
∵∠P=90°,
∴∠PHE+∠PEB=90°,
∵∠PEB=∠AEM,
∴∠PHE+∠AEM=90°,
∴∠PFD﹣∠AEM=90°;
(3)如图②,∵∠P=90°,∠PEB=15°,
∴∠PHE=∠P﹣∠PEB=90°﹣15°=75°,
∴∠BHF=∠PHE=75°,
∵AB//CD,
∴∠DFH+∠BHF=180°,
∴∠DFH=180°﹣∠BHF=105°,
∴∠OFN=∠DFH=105°,
∵∠DON=20°,
∴∠N=180°﹣∠DON﹣∠OFN=55°.
