《第1章三角形的证明》单元测试题-北师大版八年级数学下册(含解析) (3)
文档属性
| 名称 | 《第1章三角形的证明》单元测试题-北师大版八年级数学下册(含解析) (3) |  | |
| 格式 | docx | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 11:21:55 | ||
图片预览


文档简介
北师大新版八年级下册数学单元测试卷
《第1章 三角形的证明》
一.选择题
1.下列条件中,不能判定两个直角三角形全等的是( )
A.一锐角和斜边对应相等
B.两条直角边对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
2.已知等腰三角形的两边长分别为5cm、2cm,则该等腰三角形的周长是( )
A.7cm B.9cm
C.12cm或者9cm D.12cm
3.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
A.EF>BE+CF B.EF=BE+CF C.EF<BE+CF D.不能确定
4.一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )
A.等腰三角形 B.直角三角形
C.正三角形 D.等腰直角三角形
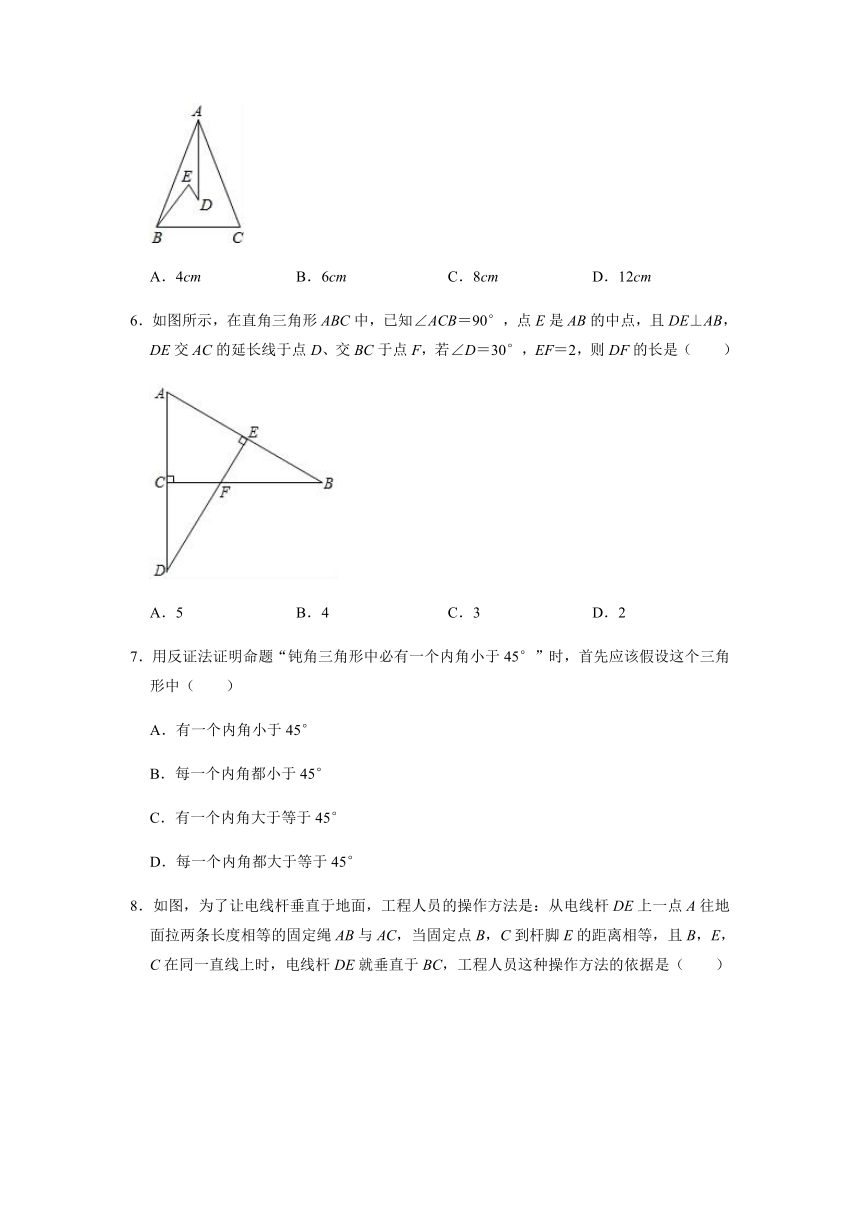
5.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )
A.4cm B.6cm C.8cm D.12cm
6.如图所示,在直角三角形ABC中,已知∠ACB=90°,点E是AB的中点,且DE⊥AB,DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A.5 B.4 C.3 D.2
7.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
8.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
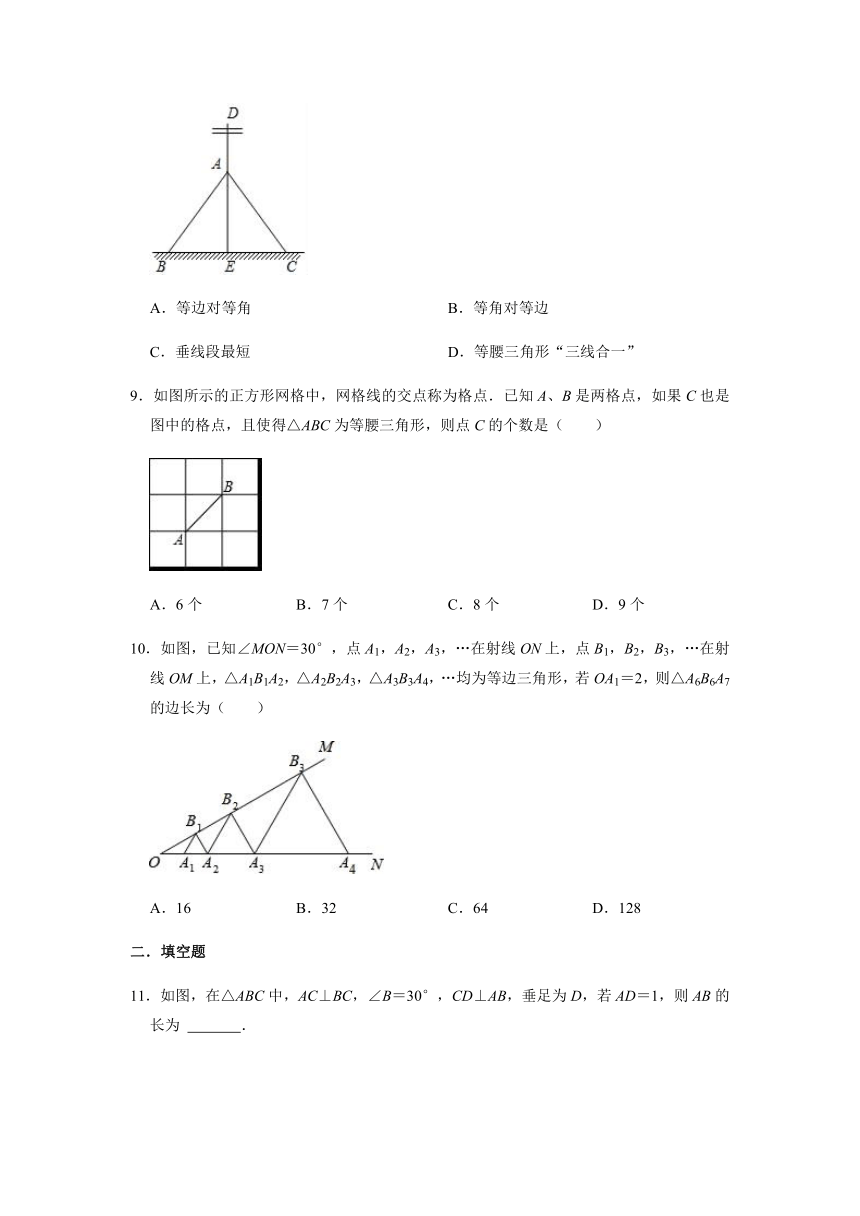
C.垂线段最短 D.等腰三角形“三线合一”
9.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
10.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( )
A.16 B.32 C.64 D.128
二.填空题
11.如图,在△ABC中,AC⊥BC,∠B=30°,CD⊥AB,垂足为D,若AD=1,则AB的长为 .
12.用反证法证明“已知,a⊥b,c⊥b,求证:a∥c”,第一步应先假设 .
13.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为 .
14.如图,△ABC中,AB=AC,AD是BC边上的高,△ABC的周长为30cm,BD=4cm,则AC的长为 cm.
15.如图,在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4cm,△ABC的周长为26cm,则△BCE的周长为 cm.
16.如图,△ABC中,AB=6,AC=7,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于E、F,则△AEF的周长为 .
17.如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD= .
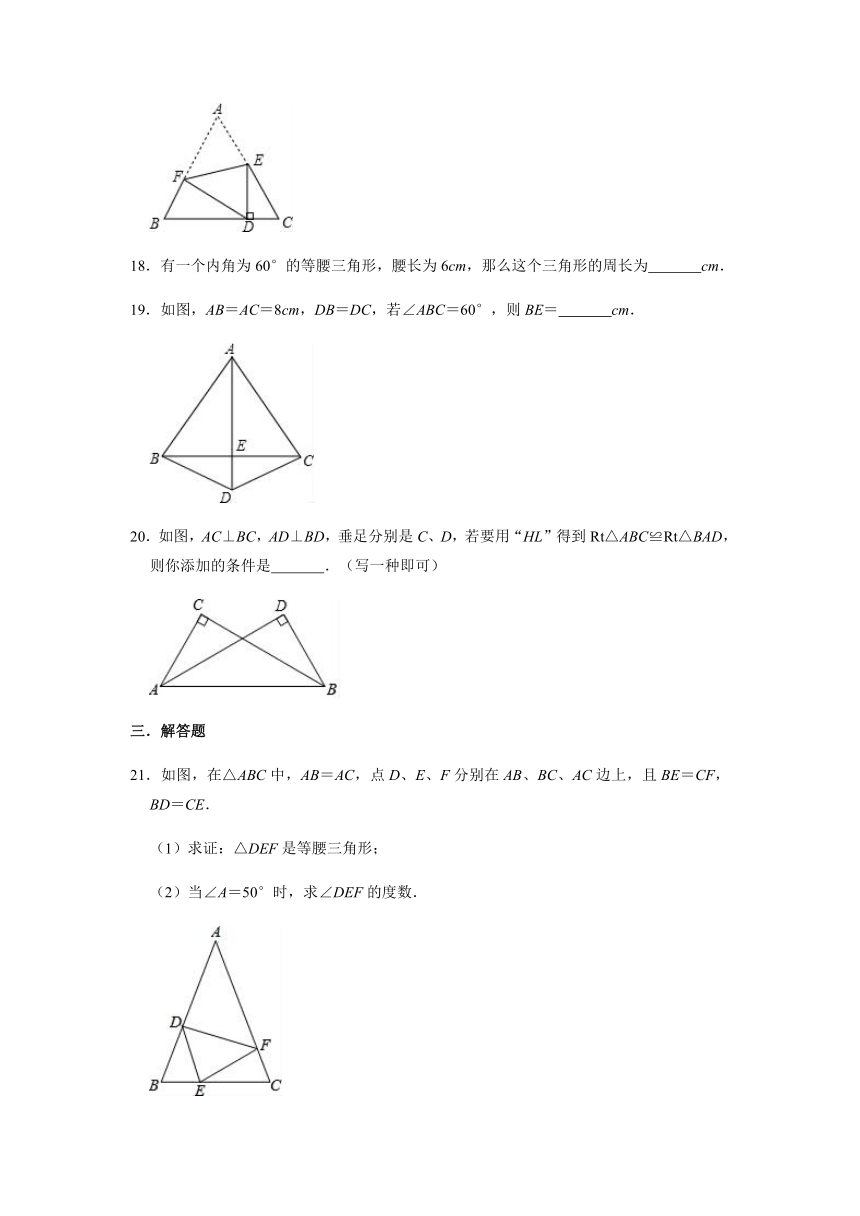
18.有一个内角为60°的等腰三角形,腰长为6cm,那么这个三角形的周长为 cm.
19.如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE= cm.
20.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是 .(写一种即可)
三.解答题
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
22.如图:△ABC和△ADE是等边三角形.证明:BD=CE.
23.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,你能找出一对全等的三角形吗?为什么它们是全等的?
24.求证:等腰三角形两底角相等.
25.在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,求∠CDE的度数.
26.如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处.分别从A、B处望灯塔C,测得∠NAC=42°,∠NBC=84度.求B处与灯塔C距离.
参考答案与试题解析
一.选择题
1.解:A、正确.符合AAS;
B、正确.符合SAS;
C、正确.符合HL;
D、错误.要证两三角形全等必须有边的参与.
故选:D.
2.解:①5cm为腰,2cm为底,此时周长为12cm;
②5cm为底,2cm为腰,则两边和小于第三边无法构成三角形,故舍去.
∴其周长是12cm.
故选:D.
3.解:∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+FC,
故选:B.
4.解:根据等腰三角形的三线合一的性质,可得三边相等,则对这个三角形最准确的判断是正三角形.
故选:C.
5.解:延长ED交BC于M,延长AD交BC于N,
∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∵BE=6cm,DE=2cm,
∴DM=4cm,
∵△BEM为等边三角形,
∴∠EMB=60°,
∵AN⊥BC,
∴∠DNM=90°,
∴∠NDM=30°,
∴NM=2cm,
∴BN=4cm,
∴BC=2BN=8cm.
故选:C.
6.解:连接AF,
∵∠ACB=90°,DE⊥AB,
∴∠B+∠BAC=∠D+∠BAC=90°,
∴∠B=∠D=30°,
∵EF=2,
∴BF=2EF=4,
∵E为AB的中点,
∴AF=BF=4,
∴∠B=∠BAF=30°,
∴∠CAF=∠BAC﹣∠BAF=30°,
∴CF=,
又∵∠D=30°,
∴CF=DF,
∴DF=AF=4.
故选:B.
7.解:用反证法证明“钝角三角形中必有一个内角小于45°”时,
应先假设这个三角形中每一个内角都不小于45°,即每一个内角都大于或等于45°.
故选:D.
8.解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
9.解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
10.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∴∠A1B1O=∠B1A1A2﹣∠MON=60°﹣30°=30°,
∴∠A1B1O=∠MON,
∴A1B1=OA1,
∴A1B1=A1A2=OA1,
同理可得A2B2=A2A3=OA2=2OA1,
∴A3B3=A3A4=OA3=2OA2=22 OA1,
A4B4=A4A5=OA4=2OA3=23 OA1,
…
∴AnBn=AnAn+1=2n﹣1 OA1=2n,
∴△A6B6A7的边长:A6B6=26=64,
故选:C.
二.填空题
11.解:∵AC⊥BC,
∴∠ACB=90°,
∵∠B=30°,
∴∠A=60°,AB=2AC,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∴AC=2AD,
∴AB=4AD,
∵AD=1,
∴AB=4,
故答案为:4.
12.解:原命题“已知,a⊥b,c⊥b,求证:a∥c”,
用反证法时应假设结论不成立,
即假设a与c不平行(或a与c相交).
故答案为:a与c不平行(或a与c相交).
13.解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+25°=115°;
②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣25°=65°.
故答案为:115°或65°.
14.解:∵AB=AC,AD⊥BC,
∴BD=CD=4cm,
∴BC=BD+CD=8cm.
∵△ABC的周长为30cm,
∴AC=AB=(30﹣8)=11,
故答案为11.
15.解:∵ED垂直平分AB,
∴AE=BE,
∴BD=AD=4cm,AB=8cm,
∵△ABC的周长为26cm,
∴AC+BC=18cm,
△BCE的周长=BC+CE+AE=BC+CE+AE=18cm.
故填18.
16.解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=6,AC=7,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=6+7=13.
故答案为:13..
17.解:由翻折的性质可知;∠AFE=∠EFD.
∵△ABC为等边三角形,
∴∠B=60°,∠C=60°,∠A=∠EDF=60°.
∵ED⊥BC,
∴△EDC为直角三角形,
∴∠FDB=30°,
∴∠AFE+∠EFD=60°+30°=90°,
∴∠EFD=45°.
故答案为:45°
18.解:根据等边三角形的判定:有一个角是60°的等腰三角形的三角形是等边三角形.再根据等边三角形的三边相等,得这个三角形的周长是6×3=18.
故答案为18.
19.解:∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,A在BC的垂直平分线上,
∴BC=AB=8cm,
∵DB=DC,
∴点D在BC的垂直平分线上,
∴AD垂直平分BC,
∴BE=BC=4cm.
故答案为:4.
20.解:可添加AC=BD,
∵AC⊥BC,AD⊥BD,
∴∠C=∠D=90°,
在Rt△ABC和Rt△BAD中,
∵,
∴Rt△ABC≌Rt△BAD(HL),
故答案为:AC=BD.
三.解答题
21.(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
22.证明:∵△ABC和△ADE是等边三角形(已知),
∴AB=AC,AD=AE,∠BAC=∠DAE=60°(等边三角形的性质).
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC(等式的性质),即∠BAD=∠CAE.
在△BAD与△CAE中,
∵,
∴△BAD≌△CAE(SAS).
∴BD=CE(全等三角形的对应边相等).
23.解:△AED≌△AFD.
原因:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,∠EAD=∠FAD.
∵AD=AD,
∴△AED≌△AFD(AAS).
24.已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°,
在Rt△ADB和Rt△ADC中,
∴△ADB≌△ADC(HL).
∴∠B=∠C.
25.解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,
∠ADC=90°,
又∵AD=AE,
∴∠ADE==70°,
∴∠CDE=90°﹣70°=20°.
26.解:∵∠NBC是△ABC的外角
∴∠C=∠NBC﹣∠NAC=42°
∴∠C=∠BAC
∴BC=BA=18×10=180(海里)
因此B处与灯塔C距离是180海里.
《第1章 三角形的证明》
一.选择题
1.下列条件中,不能判定两个直角三角形全等的是( )
A.一锐角和斜边对应相等
B.两条直角边对应相等
C.斜边和一直角边对应相等
D.两个锐角对应相等
2.已知等腰三角形的两边长分别为5cm、2cm,则该等腰三角形的周长是( )
A.7cm B.9cm
C.12cm或者9cm D.12cm
3.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
A.EF>BE+CF B.EF=BE+CF C.EF<BE+CF D.不能确定
4.一个三角形任意一边上的高都是这边上的中线,则对这个三角形最准确的判断是( )
A.等腰三角形 B.直角三角形
C.正三角形 D.等腰直角三角形
5.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平分∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,则BC的长为( )
A.4cm B.6cm C.8cm D.12cm
6.如图所示,在直角三角形ABC中,已知∠ACB=90°,点E是AB的中点,且DE⊥AB,DE交AC的延长线于点D、交BC于点F,若∠D=30°,EF=2,则DF的长是( )
A.5 B.4 C.3 D.2
7.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45°
B.每一个内角都小于45°
C.有一个内角大于等于45°
D.每一个内角都大于等于45°
8.如图,为了让电线杆垂直于地面,工程人员的操作方法是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC,工程人员这种操作方法的依据是( )
A.等边对等角 B.等角对等边
C.垂线段最短 D.等腰三角形“三线合一”
9.如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
10.如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( )
A.16 B.32 C.64 D.128
二.填空题
11.如图,在△ABC中,AC⊥BC,∠B=30°,CD⊥AB,垂足为D,若AD=1,则AB的长为 .
12.用反证法证明“已知,a⊥b,c⊥b,求证:a∥c”,第一步应先假设 .
13.等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为 .
14.如图,△ABC中,AB=AC,AD是BC边上的高,△ABC的周长为30cm,BD=4cm,则AC的长为 cm.
15.如图,在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4cm,△ABC的周长为26cm,则△BCE的周长为 cm.
16.如图,△ABC中,AB=6,AC=7,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,交AB、AC于E、F,则△AEF的周长为 .
17.如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD= .
18.有一个内角为60°的等腰三角形,腰长为6cm,那么这个三角形的周长为 cm.
19.如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE= cm.
20.如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是 .(写一种即可)
三.解答题
21.如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=50°时,求∠DEF的度数.
22.如图:△ABC和△ADE是等边三角形.证明:BD=CE.
23.如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,你能找出一对全等的三角形吗?为什么它们是全等的?
24.求证:等腰三角形两底角相等.
25.在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,求∠CDE的度数.
26.如图,一只船从A处出发,以18海里/时的速度向正北航行,经过10小时到达B处.分别从A、B处望灯塔C,测得∠NAC=42°,∠NBC=84度.求B处与灯塔C距离.
参考答案与试题解析
一.选择题
1.解:A、正确.符合AAS;
B、正确.符合SAS;
C、正确.符合HL;
D、错误.要证两三角形全等必须有边的参与.
故选:D.
2.解:①5cm为腰,2cm为底,此时周长为12cm;
②5cm为底,2cm为腰,则两边和小于第三边无法构成三角形,故舍去.
∴其周长是12cm.
故选:D.
3.解:∵EF∥BC,
∴∠EDB=∠DBC,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∴∠EDB=∠EBD,
∴ED=BE,
同理DF=FC,
∴ED+DF=BE+FC,
即EF=BE+FC,
故选:B.
4.解:根据等腰三角形的三线合一的性质,可得三边相等,则对这个三角形最准确的判断是正三角形.
故选:C.
5.解:延长ED交BC于M,延长AD交BC于N,
∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∵BE=6cm,DE=2cm,
∴DM=4cm,
∵△BEM为等边三角形,
∴∠EMB=60°,
∵AN⊥BC,
∴∠DNM=90°,
∴∠NDM=30°,
∴NM=2cm,
∴BN=4cm,
∴BC=2BN=8cm.
故选:C.
6.解:连接AF,
∵∠ACB=90°,DE⊥AB,
∴∠B+∠BAC=∠D+∠BAC=90°,
∴∠B=∠D=30°,
∵EF=2,
∴BF=2EF=4,
∵E为AB的中点,
∴AF=BF=4,
∴∠B=∠BAF=30°,
∴∠CAF=∠BAC﹣∠BAF=30°,
∴CF=,
又∵∠D=30°,
∴CF=DF,
∴DF=AF=4.
故选:B.
7.解:用反证法证明“钝角三角形中必有一个内角小于45°”时,
应先假设这个三角形中每一个内角都不小于45°,即每一个内角都大于或等于45°.
故选:D.
8.解:∵AB=AC,BE=CE,
∴AE⊥BC,
故工程人员这种操作方法的依据是等腰三角形“三线合一”,
故选:D.
9.解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
10.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,A1B1=A1A2,
∴∠A1B1O=∠B1A1A2﹣∠MON=60°﹣30°=30°,
∴∠A1B1O=∠MON,
∴A1B1=OA1,
∴A1B1=A1A2=OA1,
同理可得A2B2=A2A3=OA2=2OA1,
∴A3B3=A3A4=OA3=2OA2=22 OA1,
A4B4=A4A5=OA4=2OA3=23 OA1,
…
∴AnBn=AnAn+1=2n﹣1 OA1=2n,
∴△A6B6A7的边长:A6B6=26=64,
故选:C.
二.填空题
11.解:∵AC⊥BC,
∴∠ACB=90°,
∵∠B=30°,
∴∠A=60°,AB=2AC,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∴AC=2AD,
∴AB=4AD,
∵AD=1,
∴AB=4,
故答案为:4.
12.解:原命题“已知,a⊥b,c⊥b,求证:a∥c”,
用反证法时应假设结论不成立,
即假设a与c不平行(或a与c相交).
故答案为:a与c不平行(或a与c相交).
13.解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部.
根据三角形的一个外角等于与它不相邻的两个内角的和,即可求得顶角是90°+25°=115°;
②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣25°=65°.
故答案为:115°或65°.
14.解:∵AB=AC,AD⊥BC,
∴BD=CD=4cm,
∴BC=BD+CD=8cm.
∵△ABC的周长为30cm,
∴AC=AB=(30﹣8)=11,
故答案为11.
15.解:∵ED垂直平分AB,
∴AE=BE,
∴BD=AD=4cm,AB=8cm,
∵△ABC的周长为26cm,
∴AC+BC=18cm,
△BCE的周长=BC+CE+AE=BC+CE+AE=18cm.
故填18.
16.解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=6,AC=7,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=6+7=13.
故答案为:13..
17.解:由翻折的性质可知;∠AFE=∠EFD.
∵△ABC为等边三角形,
∴∠B=60°,∠C=60°,∠A=∠EDF=60°.
∵ED⊥BC,
∴△EDC为直角三角形,
∴∠FDB=30°,
∴∠AFE+∠EFD=60°+30°=90°,
∴∠EFD=45°.
故答案为:45°
18.解:根据等边三角形的判定:有一个角是60°的等腰三角形的三角形是等边三角形.再根据等边三角形的三边相等,得这个三角形的周长是6×3=18.
故答案为18.
19.解:∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,A在BC的垂直平分线上,
∴BC=AB=8cm,
∵DB=DC,
∴点D在BC的垂直平分线上,
∴AD垂直平分BC,
∴BE=BC=4cm.
故答案为:4.
20.解:可添加AC=BD,
∵AC⊥BC,AD⊥BD,
∴∠C=∠D=90°,
在Rt△ABC和Rt△BAD中,
∵,
∴Rt△ABC≌Rt△BAD(HL),
故答案为:AC=BD.
三.解答题
21.(1)证明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
,
∴△BDE≌△CEF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠BED+∠CEF=∠BED+∠BDE,
∵∠B+(∠BED+∠BDE)=180°,
∠DEF+(∠BED+∠BDE)=180°,
∴∠B=∠DEF,
∵∠A=50°,AB=AC,
∴∠B=(180°﹣50°)=65°,
∴∠DEF=65°.
22.证明:∵△ABC和△ADE是等边三角形(已知),
∴AB=AC,AD=AE,∠BAC=∠DAE=60°(等边三角形的性质).
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC(等式的性质),即∠BAD=∠CAE.
在△BAD与△CAE中,
∵,
∴△BAD≌△CAE(SAS).
∴BD=CE(全等三角形的对应边相等).
23.解:△AED≌△AFD.
原因:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴∠AED=∠AFD,∠EAD=∠FAD.
∵AD=AD,
∴△AED≌△AFD(AAS).
24.已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°,
在Rt△ADB和Rt△ADC中,
∴△ADB≌△ADC(HL).
∴∠B=∠C.
25.解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,
∠ADC=90°,
又∵AD=AE,
∴∠ADE==70°,
∴∠CDE=90°﹣70°=20°.
26.解:∵∠NBC是△ABC的外角
∴∠C=∠NBC﹣∠NAC=42°
∴∠C=∠BAC
∴BC=BA=18×10=180(海里)
因此B处与灯塔C距离是180海里.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
