2021-2022学年苏科版数学七年级下册7.2探索平行线的性质课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学七年级下册7.2探索平行线的性质课堂练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 10:29:17 | ||
图片预览


文档简介
2021-2022年初中数学七年级下册同步(苏科版)
7.2探索平行线的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,,,,则( )
A.100 B.105
C.110 D.115
2.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.100° B.90° C.80° D.70°
3.和是同旁内角,,那么等于( ).A. B. C.或 D.大小不定
4.如图,则下面结论中正确的是( )
A. B. C. D.
5.如图,点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5 cm,则点M到AB的距离( )
A.大于5 cm B.小于5 cm
C.等于5 cm D.不确定
6.在“(1)同位角相等(2)两直线平行(3)是判定(4)是性质”中,语序排列有(a).(1)(2)(4);(b).(1)(2)(3);(c).(2)(1)(3);(d).(2)(1)(4),其中语序排列正确的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
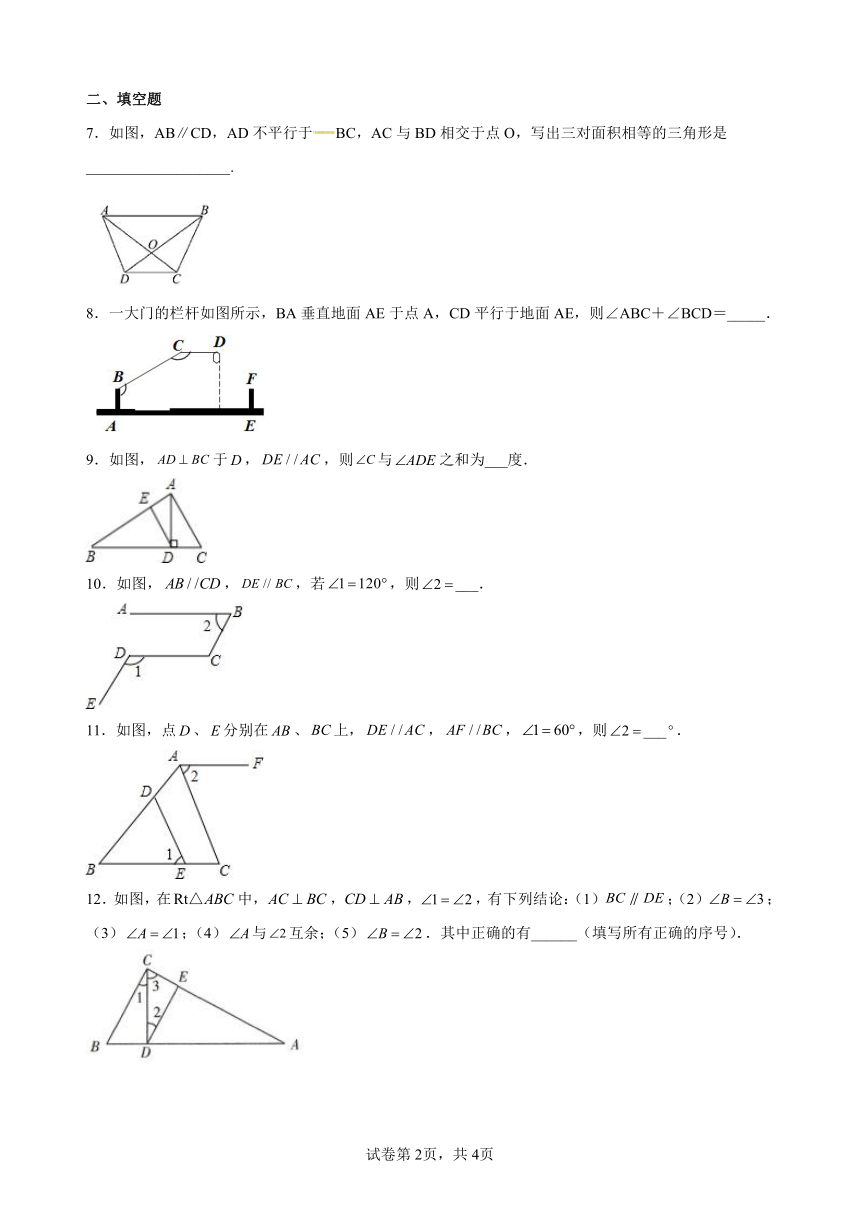
7.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
8.一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
9.如图,于,,则与之和为___度.
10.如图,,,若,则___.
11.如图,点、分别在、上,,,,则___.
12.如图,在中,,,,有下列结论:(1);(2);(3);(4)与互余;(5).其中正确的有______(填写所有正确的序号).
三、解答题
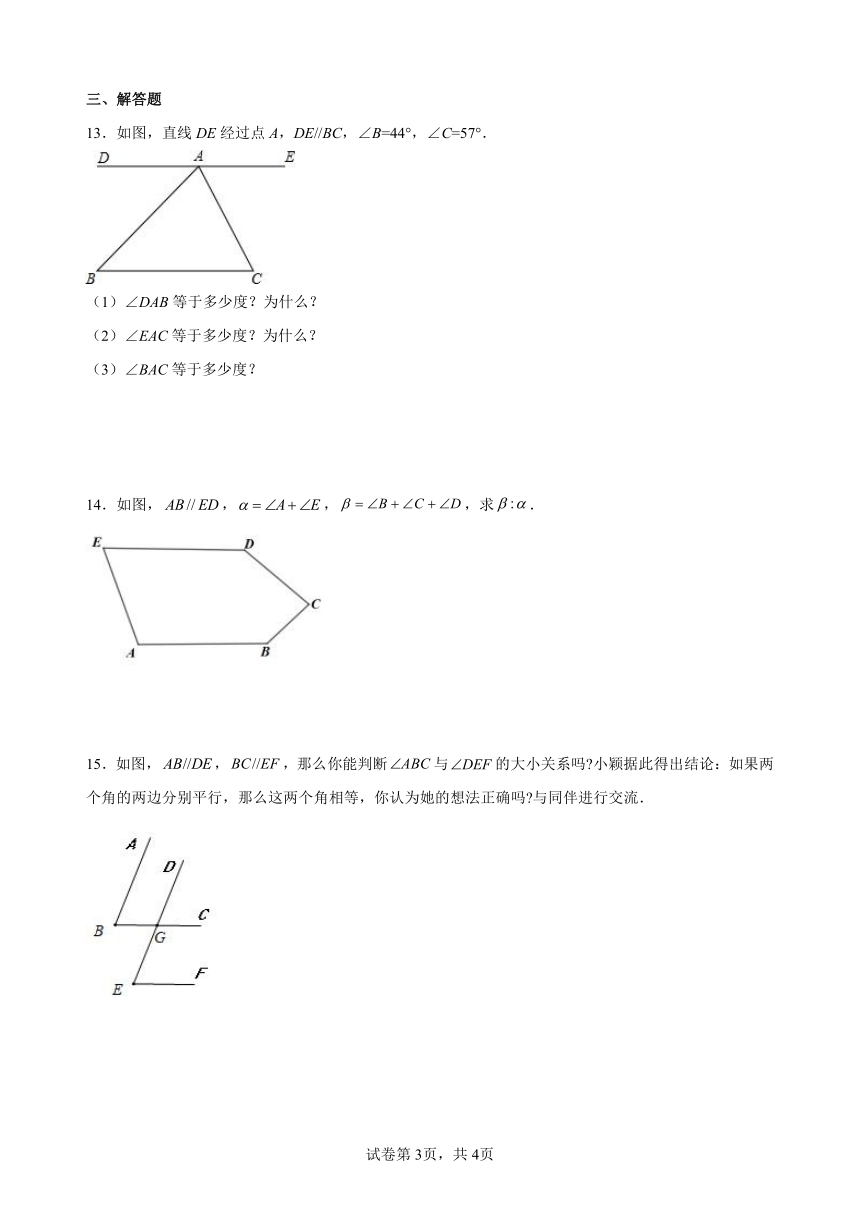
13.如图,直线DE经过点A,DE//BC,∠B=44°,∠C=57°.
(1)∠DAB等于多少度?为什么?
(2)∠EAC等于多少度?为什么?
(3)∠BAC等于多少度?
14.如图,,,,求.
15.如图,,,那么你能判断与的大小关系吗 小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗 与同伴进行交流.
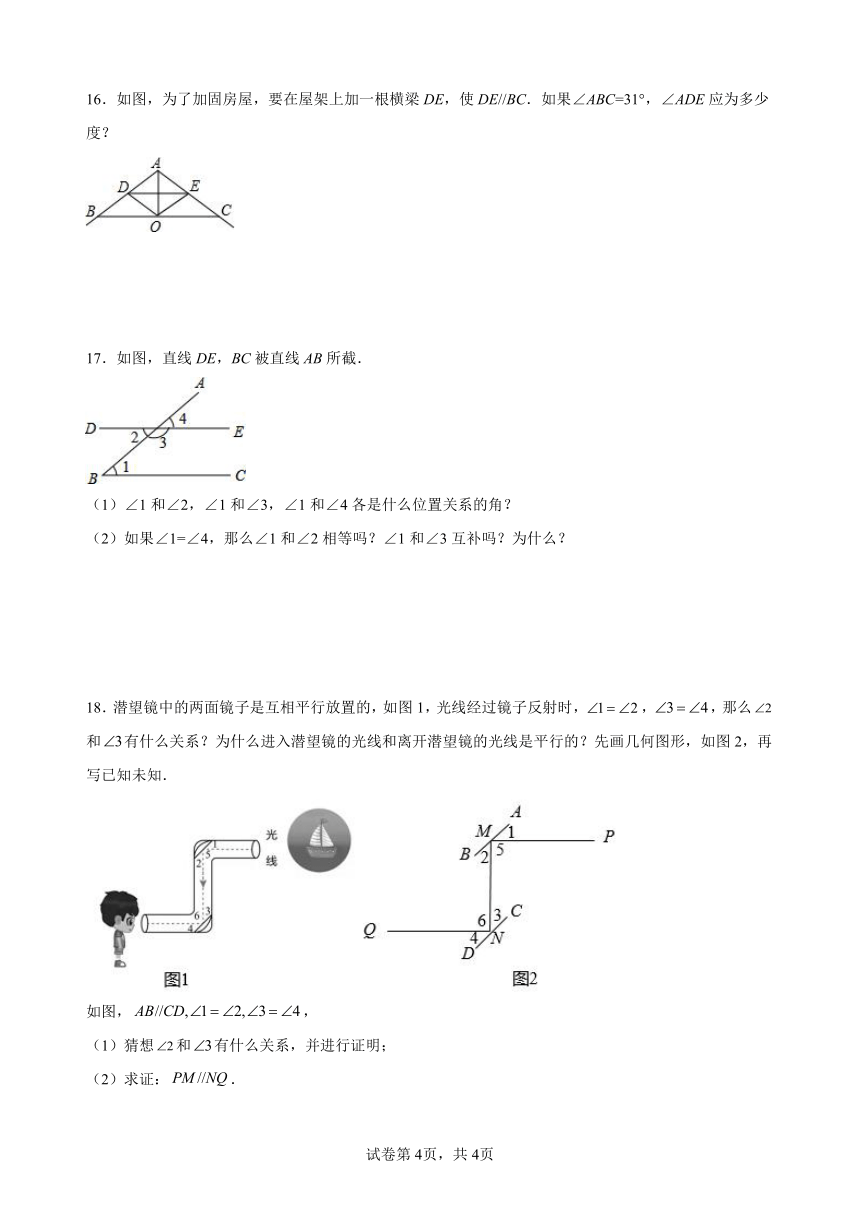
16.如图,为了加固房屋,要在屋架上加一根横梁DE,使DE//BC.如果∠ABC=31°,∠ADE应为多少度?
17.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
18.潜望镜中的两面镜子是互相平行放置的,如图1,光线经过镜子反射时,,,那么和有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?先画几何图形,如图2,再写已知未知.
如图,,
(1)猜想和有什么关系,并进行证明;
(2)求证:.
试卷第页,共页
试卷第1页,共3页
参考答案:
1.B
【解析】如图所示,作,
∵,
∴,
∴,
又∵,
∴,
∴,
故选:B.
2.A
【解析】∵AB∥CD,
∴∠DCE+∠BEF=180°,
∵∠DCE=80°,
∴∠BEF=180°-80°=100°.
故选A.
3.D
【解析】解:∵题目并未告诉,∠1和∠2是属于两条平行线被截的同旁内角,
∴∠2的度数大小不能确定,
故选D.
4.B
【解析】解:,
∴,
故选:B.
5.C
【解析】解:∵AB∥CD, 点P到CD的距离为5 cm,
∴点M到AB的距离等于5 cm,
故选C.
6.C
【解析】解:两直线平行,同位角相等是性质,同位角相等,两直线平行式判定,
∴b和d正确,
故选C.
7.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
8.270°
【解析】过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
9.90
【解析】解:,
,
,
;
.
故答案为:90
10.60°
【解析】,
,
,
,
.
故答案为:.
11.60
【解析】,
,
,
,
,
,
.
故答案为:60.
12.(1)(2)(3)
【解析】∵AC⊥BC,CD⊥AB,
∴△ACD与△ACB都为直角三角形,
∴∠B+∠1=90°,∠A+∠B=90°,
∴∠1=∠A,选项(3)正确;
∵∠1=∠2,
∴AC∥DE,选项(1)正确;
∵AC⊥BC,CD⊥AB,
∴∠B+∠1=90°,∠3+∠1=90°,
∴∠B=∠3,选项(2)正确;
∵∠1=∠A,∠1=∠2,
∴∠2=∠A,即∠2与∠A不互余,选项(4)错误;
∠2不一定等于∠B,选项(5)错误;
则正确的选项有(1)(2)(3),
故答案为(1)(2)(3).
13.(1)∠DAB =44°,见解析;(2)∠EAC=57°,见解析;(3)∠BAC=79°.
【解析】解:(1)∠DAB=44°.
理由:∵DE∥BC,
∴∠DAB=∠B=44°(两直线平行,内错角相等);
(2)∠EAC=57°,
理由:∵DE∥BC,
∴∠EAC=∠C=57°(两直线平行,内错角相等);
(3)∠BAC=180°-∠B-∠C=79°.
14.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
15.∠B=∠E;小颖的结论不全面.
【解析】解:∠ABC=∠DEF,
理由:∵ABDE,
∴∠B=∠DGC,
∵BCEF,
∴∠E=∠DGC,
∴∠B=∠E;
她的想法不对,两个角的两边分别平行,那么这两个角相等或互补;
理由:∵ABDE,
∴∠B+∠DGB=180°,
∵BCEF,
∴∠E=∠DGB,
∴∠B+∠E=180°.
16.∠ADE=31°.
【解析】解:∠ADE应为31°.
理由:∵∠ADE=31°,∠ABC=31°,
∴∠ABC=∠ADE,
∴DE∥BC(同位角相等,两直线平行),
∴∠ADE=31°.
17.(1)和是内错角,和是同旁内角,和是同位角.(2)相等,互补,理由见解析
【解析】解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角;
(2)∠1和∠2相等,∠1和∠3互补.
理由如下:
∵∠1=∠4,
∴DE∥BC,
∴∠1=∠2,∠1+∠3=180°.
18.(1),证明见解析;(2)见解析
【解析】解:(1)根据题意可知,
∴ (两直线平行,内错角相等).
(2)∵,
∴;
∵,,
∴,
∴(内错角相等,两直线平行).
试卷第页,共页
试卷第页,共页
7.2探索平行线的性质-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,,,,则( )
A.100 B.105
C.110 D.115
2.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.100° B.90° C.80° D.70°
3.和是同旁内角,,那么等于( ).A. B. C.或 D.大小不定
4.如图,则下面结论中正确的是( )
A. B. C. D.
5.如图,点P,M分别在直线AB和直线CD上,且AB∥CD,点P到CD的距离为5 cm,则点M到AB的距离( )
A.大于5 cm B.小于5 cm
C.等于5 cm D.不确定
6.在“(1)同位角相等(2)两直线平行(3)是判定(4)是性质”中,语序排列有(a).(1)(2)(4);(b).(1)(2)(3);(c).(2)(1)(3);(d).(2)(1)(4),其中语序排列正确的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
7.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是___________________.
8.一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
9.如图,于,,则与之和为___度.
10.如图,,,若,则___.
11.如图,点、分别在、上,,,,则___.
12.如图,在中,,,,有下列结论:(1);(2);(3);(4)与互余;(5).其中正确的有______(填写所有正确的序号).
三、解答题
13.如图,直线DE经过点A,DE//BC,∠B=44°,∠C=57°.
(1)∠DAB等于多少度?为什么?
(2)∠EAC等于多少度?为什么?
(3)∠BAC等于多少度?
14.如图,,,,求.
15.如图,,,那么你能判断与的大小关系吗 小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等,你认为她的想法正确吗 与同伴进行交流.
16.如图,为了加固房屋,要在屋架上加一根横梁DE,使DE//BC.如果∠ABC=31°,∠ADE应为多少度?
17.如图,直线DE,BC被直线AB所截.
(1)∠1和∠2,∠1和∠3,∠1和∠4各是什么位置关系的角?
(2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
18.潜望镜中的两面镜子是互相平行放置的,如图1,光线经过镜子反射时,,,那么和有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?先画几何图形,如图2,再写已知未知.
如图,,
(1)猜想和有什么关系,并进行证明;
(2)求证:.
试卷第页,共页
试卷第1页,共3页
参考答案:
1.B
【解析】如图所示,作,
∵,
∴,
∴,
又∵,
∴,
∴,
故选:B.
2.A
【解析】∵AB∥CD,
∴∠DCE+∠BEF=180°,
∵∠DCE=80°,
∴∠BEF=180°-80°=100°.
故选A.
3.D
【解析】解:∵题目并未告诉,∠1和∠2是属于两条平行线被截的同旁内角,
∴∠2的度数大小不能确定,
故选D.
4.B
【解析】解:,
∴,
故选:B.
5.C
【解析】解:∵AB∥CD, 点P到CD的距离为5 cm,
∴点M到AB的距离等于5 cm,
故选C.
6.C
【解析】解:两直线平行,同位角相等是性质,同位角相等,两直线平行式判定,
∴b和d正确,
故选C.
7.△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.
8.270°
【解析】过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
9.90
【解析】解:,
,
,
;
.
故答案为:90
10.60°
【解析】,
,
,
,
.
故答案为:.
11.60
【解析】,
,
,
,
,
,
.
故答案为:60.
12.(1)(2)(3)
【解析】∵AC⊥BC,CD⊥AB,
∴△ACD与△ACB都为直角三角形,
∴∠B+∠1=90°,∠A+∠B=90°,
∴∠1=∠A,选项(3)正确;
∵∠1=∠2,
∴AC∥DE,选项(1)正确;
∵AC⊥BC,CD⊥AB,
∴∠B+∠1=90°,∠3+∠1=90°,
∴∠B=∠3,选项(2)正确;
∵∠1=∠A,∠1=∠2,
∴∠2=∠A,即∠2与∠A不互余,选项(4)错误;
∠2不一定等于∠B,选项(5)错误;
则正确的选项有(1)(2)(3),
故答案为(1)(2)(3).
13.(1)∠DAB =44°,见解析;(2)∠EAC=57°,见解析;(3)∠BAC=79°.
【解析】解:(1)∠DAB=44°.
理由:∵DE∥BC,
∴∠DAB=∠B=44°(两直线平行,内错角相等);
(2)∠EAC=57°,
理由:∵DE∥BC,
∴∠EAC=∠C=57°(两直线平行,内错角相等);
(3)∠BAC=180°-∠B-∠C=79°.
14.2:1
【解析】解:过C点作CF∥AB,
∵AB∥ED,
∴CF∥DE,
∴∠B+∠2=∠D+∠1=180°,
∴β=∠B+∠BCD+∠D=∠B+∠2+∠D+∠1=360°,
∵AB∥DE,
∴∠A+∠E=α=180°,
∴β:α=360°:180°=2:1,
15.∠B=∠E;小颖的结论不全面.
【解析】解:∠ABC=∠DEF,
理由:∵ABDE,
∴∠B=∠DGC,
∵BCEF,
∴∠E=∠DGC,
∴∠B=∠E;
她的想法不对,两个角的两边分别平行,那么这两个角相等或互补;
理由:∵ABDE,
∴∠B+∠DGB=180°,
∵BCEF,
∴∠E=∠DGB,
∴∠B+∠E=180°.
16.∠ADE=31°.
【解析】解:∠ADE应为31°.
理由:∵∠ADE=31°,∠ABC=31°,
∴∠ABC=∠ADE,
∴DE∥BC(同位角相等,两直线平行),
∴∠ADE=31°.
17.(1)和是内错角,和是同旁内角,和是同位角.(2)相等,互补,理由见解析
【解析】解:(1)∠1和∠2是内错角,∠1和∠3是同旁内角,∠1和∠4是同位角;
(2)∠1和∠2相等,∠1和∠3互补.
理由如下:
∵∠1=∠4,
∴DE∥BC,
∴∠1=∠2,∠1+∠3=180°.
18.(1),证明见解析;(2)见解析
【解析】解:(1)根据题意可知,
∴ (两直线平行,内错角相等).
(2)∵,
∴;
∵,,
∴,
∴(内错角相等,两直线平行).
试卷第页,共页
试卷第页,共页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
