2021-2022学年苏科版数学七年级下册7.5多边形的内角和与外角和课堂练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学七年级下册7.5多边形的内角和与外角和课堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 00:00:00 | ||
图片预览



文档简介
2021-2022年初中数学七年级下册同步(苏科版)
7.5多边形的内角和与外角和-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个正多边形的每个外角都是36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
2.在五边形中,,DP、CP分别平分,,则的度数是( ).A. B. C. D.
3.如果一个多边形内角和是外角和的4倍,那么这个多边形有( )条对角线.
A.20 B.27 C.35 D.44
4.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
6.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果,那么( )
A. B. C. D.
二、填空题
7.如图,设、、是的外角,则____________.
8.如果一个多边形的每个外角都等于,那么这个多边形的内角和是______度.
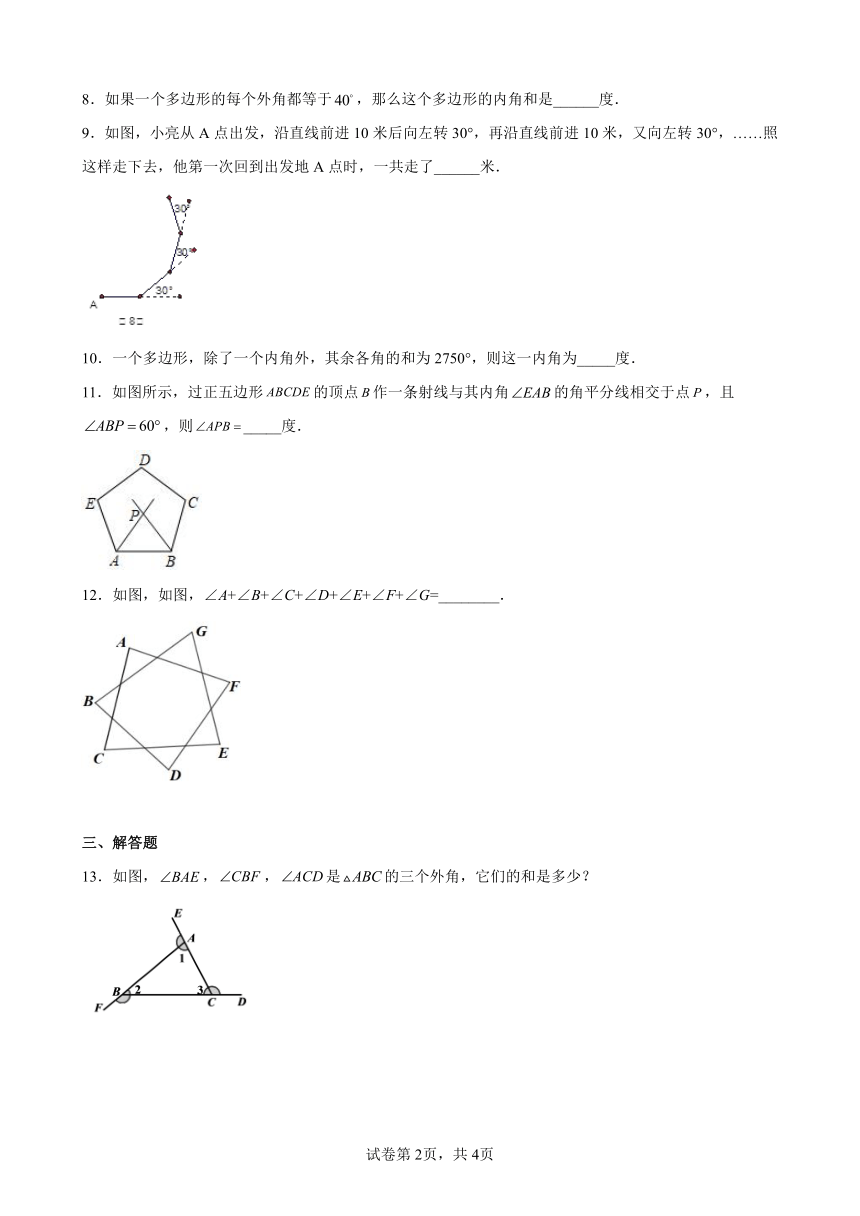
9.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了______米.
10.一个多边形,除了一个内角外,其余各角的和为2750°,则这一内角为_____度.
11.如图所示,过正五边形的顶点作一条射线与其内角的角平分线相交于点,且,则_____度.
12.如图,如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=________.
三、解答题
13.如图,,,是的三个外角,它们的和是多少?
14.小彬求出一个正多边形的一个内角为.他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
15.多边形的内角和与某一个外角的度数和为1350度.
(1)求多边形的边数;
(2)此多边形必有一内角为多少度?
16.如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
(2)求出这个图形的内角和.
17.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;
(2)AM⊥CD.
18.如图,从四边形ABCD中剪去一个三角形(只剪一刀),剩余的部分是几边形?请画出示意图(边数相同的情况只需画一个示意图),并在图形下方写上剩余部分多边形的内角和.
莉莉的解法:从四边形中剪去一个三角形,剩余部分是三角形,其内角和为.
佳佳的解法:剩余部分是四边形,其内角和为.
请问莉莉和佳佳的解法是否正确?如果不正确,请写出正确解法.
试卷第页,共页
试卷第1页,共3页
参考答案:
1.C
【解析】解:,
是正十边形.
故选:C.
2.D
【解析】解:∵在五边形ABCDE中,内角和为(5 2) 180°=540°,∠A+∠B+∠E=280°,
∴∠EDC+∠BCD=260°,
又∵DP、CP分别平分∠EDC、∠BCD,
∴∠PDC+∠PCD=130°,
∴△CDP中,∠P=180° (∠PDC+∠PCD)=180° 130°=50°
故选D.
3.C
【解析】解:设这个多边形是n边形,
根据题意得,(n-2) 180°=4×360°,
解得n=10.
10×(10-3)÷2=35(条).
故选:C.
4.B
【解析】如图,延长BA到点O,
∵六边形ABCDEF是正六边形,
∴∠FAO==60°,
∵五边形ABGHI是正五边形,
∴∠IAO==72°,
∴∠FAI=∠IAO-∠FAO=12°,
故选B.
5.D
【解析】设内角和为1080°的多边形的边数是n,则(n﹣2) 180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
6.C
【解析】解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为,
∴中间阴影部分的三角形的三个外角的度数分别为,
∵三角形的外角和为,
∴.
,
故选C.
7.360°
【解析】解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
8.1260
【解析】解:∵多边形的每一个外角都等于,
∴它的边数为:,
∴它的内角和:,
故答案为:.
9.120
【解析】 ∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.
10.130
【解析】设多边形的边数为x,由题意有
解得
因而多边形的边数是18,
则这一内角为
故答案为
11.66
【解析】解:∵五边形为正五边形,
∴度,
∵是的角平分线,
∴度,
∵,
∴.
故答案为66.
12.
【解析】解:如图,连接BC、AD.
在四边形BCEG中,得∠E+∠G+∠ECB+∠GBC=360°,
又因为∠1+∠2=∠3+∠4,∠5+∠6+∠F=180°,
∠4+∠5+∠3+∠6=∠CAF+∠BDF,即∠1+∠2+∠5+∠6=∠CAF+∠BDF,
所以∠CAF+∠B+∠C+∠BDF+∠E+∠F+∠G=540°,
即∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
故答案为:540°.
13.
【解析】解:由三角形的一个外角等于与它不相邻的两个内角之和,得
,
,
,
∴,
又∵,
∴.
14.不正确,理由见解析
【解析】不正确.
理由:设该正多边形的边数为n,如果结果正确,应有,
解方程得,
不符合题意.
15.(1)九边形(2)90°
【解析】(1)设这个外角度数为x,根据题意,得
(n-2)×180°+x°=1350°,
解得:x°=1350°-180°n+360°=1710°-180°n,
由于0<x°<180°,即0<1710°-180°n<180°,
解得8.5<n<9.5,
所以n=9.
(2)可得x°=1350°-(9-2)×180°=90°
该多边形必有一内角度数为180°-90°=90°.
16.(1)走过的路径是一个边长为6的正六边形;(2)720°.
【解析】(1)从A点出发,每走6m向左转60°,
走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6﹣2)×180°=720°.
17.见解析
【解析】解:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
18.莉莉和佳佳的解法不正确,正确解法见解析
【解析】莉莉和佳佳的解法不正确,正确解法如下:
如图(1),剩余部分是三角形,其内角和为.
如图(2),剩余部分是四边形,其内角和为.
如图(3),剩余部分是五边形,其内角和为.
图(1) 图(2) 图(3)
试卷第页,共页
试卷第页,共页
7.5多边形的内角和与外角和-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个正多边形的每个外角都是36°,那么它是( )
A.正六边形 B.正八边形 C.正十边形 D.正十二边形
2.在五边形中,,DP、CP分别平分,,则的度数是( ).A. B. C. D.
3.如果一个多边形内角和是外角和的4倍,那么这个多边形有( )条对角线.
A.20 B.27 C.35 D.44
4.如图所示,在正六边形内,以为边作正五边形,则( )
A. B. C. D.
5.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
A.7 B.7或8 C.8或9 D.7或8或9
6.将正三角形、正四边形、正五边形按如图所示的位置摆放,如果,那么( )
A. B. C. D.
二、填空题
7.如图,设、、是的外角,则____________.
8.如果一个多边形的每个外角都等于,那么这个多边形的内角和是______度.
9.如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了______米.
10.一个多边形,除了一个内角外,其余各角的和为2750°,则这一内角为_____度.
11.如图所示,过正五边形的顶点作一条射线与其内角的角平分线相交于点,且,则_____度.
12.如图,如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=________.
三、解答题
13.如图,,,是的三个外角,它们的和是多少?
14.小彬求出一个正多边形的一个内角为.他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
15.多边形的内角和与某一个外角的度数和为1350度.
(1)求多边形的边数;
(2)此多边形必有一内角为多少度?
16.如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
(2)求出这个图形的内角和.
17.如图,已知正五边形ABCDE,M是CD的中点,连接AC,BE,AM.
求证:(1)AC=BE;
(2)AM⊥CD.
18.如图,从四边形ABCD中剪去一个三角形(只剪一刀),剩余的部分是几边形?请画出示意图(边数相同的情况只需画一个示意图),并在图形下方写上剩余部分多边形的内角和.
莉莉的解法:从四边形中剪去一个三角形,剩余部分是三角形,其内角和为.
佳佳的解法:剩余部分是四边形,其内角和为.
请问莉莉和佳佳的解法是否正确?如果不正确,请写出正确解法.
试卷第页,共页
试卷第1页,共3页
参考答案:
1.C
【解析】解:,
是正十边形.
故选:C.
2.D
【解析】解:∵在五边形ABCDE中,内角和为(5 2) 180°=540°,∠A+∠B+∠E=280°,
∴∠EDC+∠BCD=260°,
又∵DP、CP分别平分∠EDC、∠BCD,
∴∠PDC+∠PCD=130°,
∴△CDP中,∠P=180° (∠PDC+∠PCD)=180° 130°=50°
故选D.
3.C
【解析】解:设这个多边形是n边形,
根据题意得,(n-2) 180°=4×360°,
解得n=10.
10×(10-3)÷2=35(条).
故选:C.
4.B
【解析】如图,延长BA到点O,
∵六边形ABCDEF是正六边形,
∴∠FAO==60°,
∵五边形ABGHI是正五边形,
∴∠IAO==72°,
∴∠FAI=∠IAO-∠FAO=12°,
故选B.
5.D
【解析】设内角和为1080°的多边形的边数是n,则(n﹣2) 180°=1080°,解得:n=8.
则原多边形的边数为7或8或9.故选D.
6.C
【解析】解:如图所示,正三角形、正四边形、正五边形的每个内角的度数分别为,
∴中间阴影部分的三角形的三个外角的度数分别为,
∵三角形的外角和为,
∴.
,
故选C.
7.360°
【解析】解:∵三角形的外角和为360°,
∴∠1+∠2+∠3=360°,
故答案为:360°.
8.1260
【解析】解:∵多边形的每一个外角都等于,
∴它的边数为:,
∴它的内角和:,
故答案为:.
9.120
【解析】 ∵360÷30=12,∴他需要走12次才会回到原来的起点,即一共走了12×10=120米.
10.130
【解析】设多边形的边数为x,由题意有
解得
因而多边形的边数是18,
则这一内角为
故答案为
11.66
【解析】解:∵五边形为正五边形,
∴度,
∵是的角平分线,
∴度,
∵,
∴.
故答案为66.
12.
【解析】解:如图,连接BC、AD.
在四边形BCEG中,得∠E+∠G+∠ECB+∠GBC=360°,
又因为∠1+∠2=∠3+∠4,∠5+∠6+∠F=180°,
∠4+∠5+∠3+∠6=∠CAF+∠BDF,即∠1+∠2+∠5+∠6=∠CAF+∠BDF,
所以∠CAF+∠B+∠C+∠BDF+∠E+∠F+∠G=540°,
即∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.
故答案为:540°.
13.
【解析】解:由三角形的一个外角等于与它不相邻的两个内角之和,得
,
,
,
∴,
又∵,
∴.
14.不正确,理由见解析
【解析】不正确.
理由:设该正多边形的边数为n,如果结果正确,应有,
解方程得,
不符合题意.
15.(1)九边形(2)90°
【解析】(1)设这个外角度数为x,根据题意,得
(n-2)×180°+x°=1350°,
解得:x°=1350°-180°n+360°=1710°-180°n,
由于0<x°<180°,即0<1710°-180°n<180°,
解得8.5<n<9.5,
所以n=9.
(2)可得x°=1350°-(9-2)×180°=90°
该多边形必有一内角度数为180°-90°=90°.
16.(1)走过的路径是一个边长为6的正六边形;(2)720°.
【解析】(1)从A点出发,每走6m向左转60°,
走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6﹣2)×180°=720°.
17.见解析
【解析】解:(1)由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠BAE,AB=BC,
∴△ABC≌△EAB,∴AC=BE.
(2)连接AD,由五边形ABCDE是正五边形,得AB=AE,∠ABC=∠AED,BC=ED,
∴△ABC≌△AED,
∴AC=AD.
又∵M是CD的中点,
∴AM⊥CD.
18.莉莉和佳佳的解法不正确,正确解法见解析
【解析】莉莉和佳佳的解法不正确,正确解法如下:
如图(1),剩余部分是三角形,其内角和为.
如图(2),剩余部分是四边形,其内角和为.
如图(3),剩余部分是五边形,其内角和为.
图(1) 图(2) 图(3)
试卷第页,共页
试卷第页,共页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
