2021—2022学年人教版八年级数学下册17.1勾股定理课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册17.1勾股定理课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 509.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 12:52:57 | ||
图片预览


文档简介
第十七章勾股定理 17.1 勾股定理 课后练习
一、选择题
1.下列各组数中是勾股数的是( )
A.1,, B.,, C.,, D.,,
2.在平面直角坐标系中,已知点A(-2,5),点B(1,1),则线段AB的长度为( )
A.2 B.3 C.4 D.5
3.一个直角三角形有两边长为3cm,4cm,则这个三角形的另一边为( )
A.5cm B.cm C.7cm D.5cm或cm
4.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
5.在中,,,.下列关于的四种说法:①是无理数;②可以用数轴上的一个点来表示;③是8的算术平方根;④.其中,所有正确的说法的序号是( )
A.①②④ B.②③④ C.①②③ D.①③④
6如图,铁路 和公路 在点 处交汇,,公路 上 处距离 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 千米/时的速度行驶时, 处受噪音影响的时间为
A. 秒 B. 秒 C. 秒 D. 秒
7如图,在 中, 是 边上的中点,连接 ,把 沿 翻折,得到 , 与 交于点 ,连接 ,若 ,,则点 到 的距离为
A. B. C. D.
8在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为如图,有一架秋千,当它静止时,踏板离地的距离 为 尺.将它往前水平推送 尺时(即 尺),秋千的踏板就和身高 尺的人一样高,即 尺.若运动过程中秋千的绳索始终拉得很直,则绳索 长为
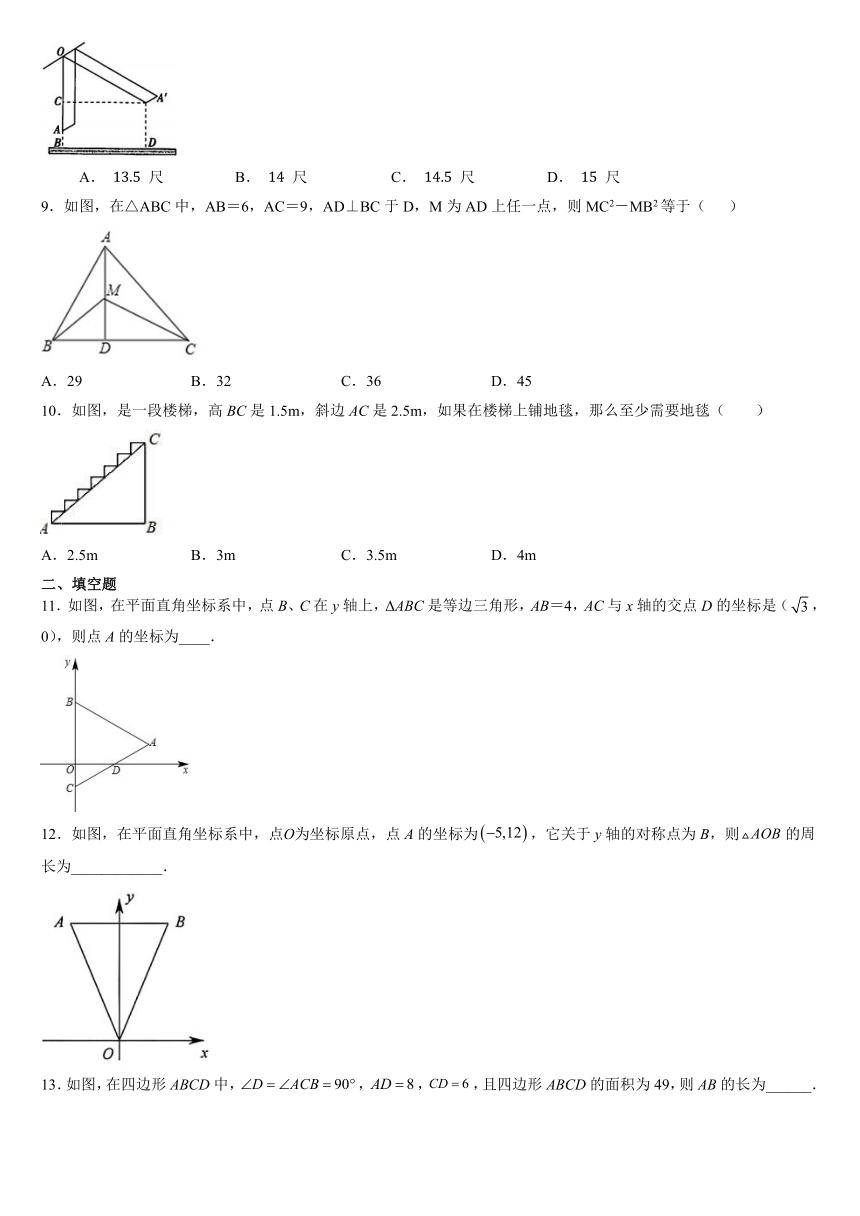
A. 尺 B. 尺 C. 尺 D. 尺
9.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
10.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m B.3m C.3.5m D.4m
二、填空题
11.如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是(,0),则点A的坐标为____.
12.如图,在平面直角坐标系中,点О为坐标原点,点A的坐标为,它关于y轴的对称点为B,则的周长为____________.
13.如图,在四边形ABCD中,,,,且四边形ABCD的面积为49,则AB的长为______.
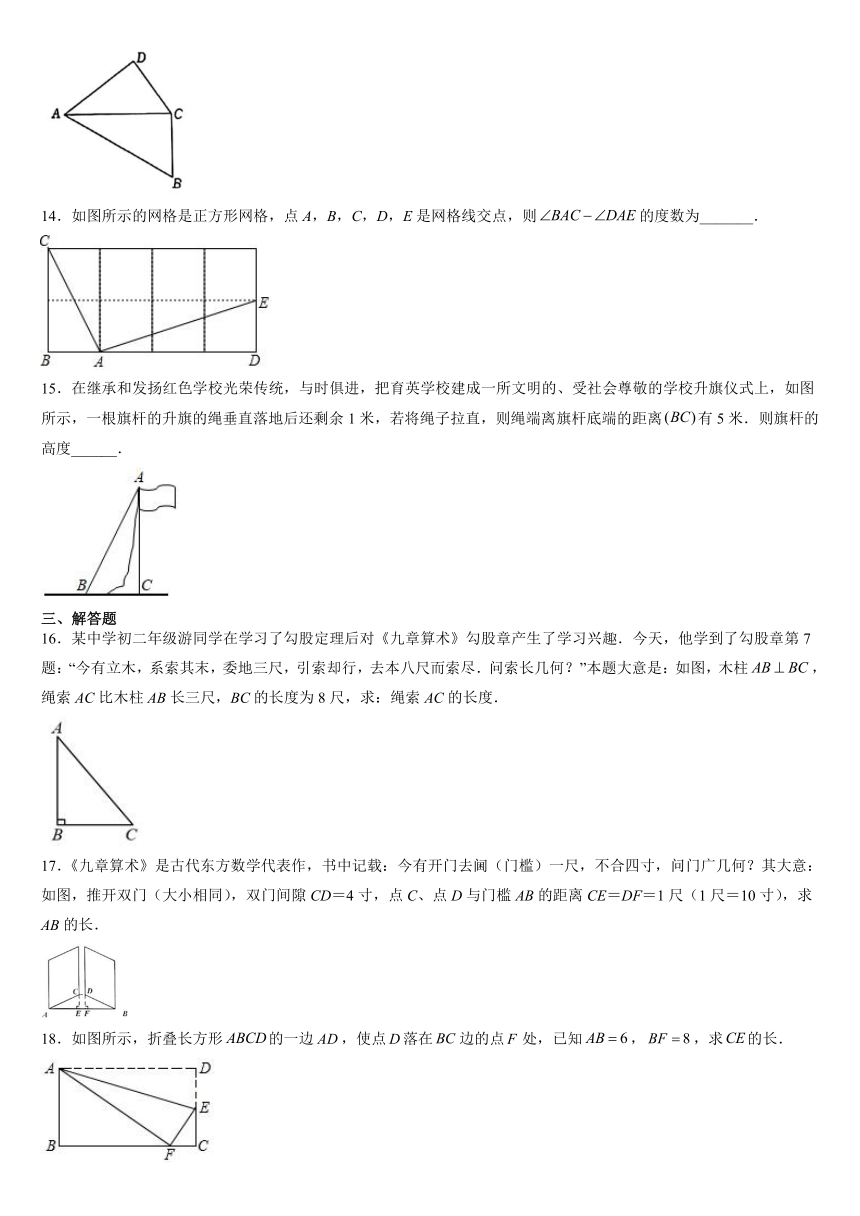
14.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则的度数为_______.
15.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
19.已知中,=90°,如图,作三个等腰直角三角形,,,,,为斜边,阴影部分的面积分别为,,,.
(1)当=6,=8时,
①求的值;
②求--的值;
(2)请写出,,,之间的数量关系,并说明理由.
20.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
21.如图,△ABC中,∠C=90°,BC=6,∠ABC的平分线与线段AC交于点D,且有AD=BD,点E是线段AB上的动点(与A、B不重合),联结DE,设AE=x,DE=y.
(1)求∠A的度数;
(2)求y关于x的函数解析式(无需写出定义域);
(3)当△BDE是等腰三角形时,求AE的长.
22.如图1和图2,在△ABC中,AB=AC,BC=8,tanC=,点M在AB上,且AM=2.点P从点M出发沿折线MB﹣BC匀速移动,不与点C重合,点Q在边AC上,点P运动的过程中始终保持∠APQ=∠B.
(1)当点P在BC上时,求点P与点A的最短距离;
(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长.
(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,直接写出点P到直线AC的距离(用含x的式子表示).
23.如图,小区有一块四边形空地,其中.为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点作了垂直于的小路.经测量,,,.
(1)求这块空地的面积.
(2)求小路的长.(答案可含根号).
(3)若每平方米草皮需要2千元(不足1平米按1平米算),则种植这片草皮最少需要多少元?
【参考答案】
1.B 2.D 3.D 4.A5.C 6.B 7.B 8.C 9.D 10.C
11.
12.36
13.
14.45°
15.12米
16.绳索长是尺
17.52寸
18.
19.解:(1)①是等腰直角三角形,=6,
==,
;
②=90°,=6,=8,
=10,
和是等腰直角三角形,
,,
设
;
(2)设,
如图,等腰直角三角形的面积公式,
∵等腰直角三角形,,,
∴,
∵,
∴,即,
∴,
∴.
20.解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
21.(1)30°;(2)y=;(3)12﹣4或8
22.(1)当点P在BC上时,PA⊥BC时,点P到A的最短距离为3;(2);(3)PJ=
23.(1);(2);(3)14000元
一、选择题
1.下列各组数中是勾股数的是( )
A.1,, B.,, C.,, D.,,
2.在平面直角坐标系中,已知点A(-2,5),点B(1,1),则线段AB的长度为( )
A.2 B.3 C.4 D.5
3.一个直角三角形有两边长为3cm,4cm,则这个三角形的另一边为( )
A.5cm B.cm C.7cm D.5cm或cm
4.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
5.在中,,,.下列关于的四种说法:①是无理数;②可以用数轴上的一个点来表示;③是8的算术平方根;④.其中,所有正确的说法的序号是( )
A.①②④ B.②③④ C.①②③ D.①③④
6如图,铁路 和公路 在点 处交汇,,公路 上 处距离 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 千米/时的速度行驶时, 处受噪音影响的时间为
A. 秒 B. 秒 C. 秒 D. 秒
7如图,在 中, 是 边上的中点,连接 ,把 沿 翻折,得到 , 与 交于点 ,连接 ,若 ,,则点 到 的距离为
A. B. C. D.
8在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几.”此问题可理解为如图,有一架秋千,当它静止时,踏板离地的距离 为 尺.将它往前水平推送 尺时(即 尺),秋千的踏板就和身高 尺的人一样高,即 尺.若运动过程中秋千的绳索始终拉得很直,则绳索 长为
A. 尺 B. 尺 C. 尺 D. 尺
9.如图,在△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A.29 B.32 C.36 D.45
10.如图,是一段楼梯,高BC是1.5m,斜边AC是2.5m,如果在楼梯上铺地毯,那么至少需要地毯( )
A.2.5m B.3m C.3.5m D.4m
二、填空题
11.如图,在平面直角坐标系中,点B、C在y轴上,ΔABC是等边三角形,AB=4,AC与x轴的交点D的坐标是(,0),则点A的坐标为____.
12.如图,在平面直角坐标系中,点О为坐标原点,点A的坐标为,它关于y轴的对称点为B,则的周长为____________.
13.如图,在四边形ABCD中,,,,且四边形ABCD的面积为49,则AB的长为______.
14.如图所示的网格是正方形网格,点A,B,C,D,E是网格线交点,则的度数为_______.
15.在继承和发扬红色学校光荣传统,与时俱进,把育英学校建成一所文明的、受社会尊敬的学校升旗仪式上,如图所示,一根旗杆的升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离有5米.则旗杆的高度______.
三、解答题
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
19.已知中,=90°,如图,作三个等腰直角三角形,,,,,为斜边,阴影部分的面积分别为,,,.
(1)当=6,=8时,
①求的值;
②求--的值;
(2)请写出,,,之间的数量关系,并说明理由.
20.如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题:
(1)求线段DE的长度;
(2)若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .
21.如图,△ABC中,∠C=90°,BC=6,∠ABC的平分线与线段AC交于点D,且有AD=BD,点E是线段AB上的动点(与A、B不重合),联结DE,设AE=x,DE=y.
(1)求∠A的度数;
(2)求y关于x的函数解析式(无需写出定义域);
(3)当△BDE是等腰三角形时,求AE的长.
22.如图1和图2,在△ABC中,AB=AC,BC=8,tanC=,点M在AB上,且AM=2.点P从点M出发沿折线MB﹣BC匀速移动,不与点C重合,点Q在边AC上,点P运动的过程中始终保持∠APQ=∠B.
(1)当点P在BC上时,求点P与点A的最短距离;
(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长.
(3)设点P移动的路程为x,当0≤x≤3及3<x≤9时,直接写出点P到直线AC的距离(用含x的式子表示).
23.如图,小区有一块四边形空地,其中.为响应沙区创文,美化小区的号召,小区计划将这块四边形空地进行规划整理.过点作了垂直于的小路.经测量,,,.
(1)求这块空地的面积.
(2)求小路的长.(答案可含根号).
(3)若每平方米草皮需要2千元(不足1平米按1平米算),则种植这片草皮最少需要多少元?
【参考答案】
1.B 2.D 3.D 4.A5.C 6.B 7.B 8.C 9.D 10.C
11.
12.36
13.
14.45°
15.12米
16.绳索长是尺
17.52寸
18.
19.解:(1)①是等腰直角三角形,=6,
==,
;
②=90°,=6,=8,
=10,
和是等腰直角三角形,
,,
设
;
(2)设,
如图,等腰直角三角形的面积公式,
∵等腰直角三角形,,,
∴,
∵,
∴,即,
∴,
∴.
20.解:(1)长方形纸片ABCD中,折叠纸片,使点D落在BC边上的点F处,
则AF=AD=BC=10,
BF=,
FC=BC BF=10 6=4,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴DE=EF,
设DE=EF=x,
则EC=DC DE=8 x,
又∵△EFC为直角三角形,
∴FC2+EC2=FE2,
即42+(8 x)2=x2,
∴x=5,
∴DE=5;
(2)连接BP,PF,PD,BD,
∵折叠纸片,使点D落在BC边上的点F处,折痕为AE,
∴D、F关于AE对称,
∴PF=PD,
则BP+PF=BP+PD≥BD,
∴BP+PF最小为BD,
BD=,
∴BP+PF最小值为:.
故答案为:.
21.(1)30°;(2)y=;(3)12﹣4或8
22.(1)当点P在BC上时,PA⊥BC时,点P到A的最短距离为3;(2);(3)PJ=
23.(1);(2);(3)14000元
