2021—2022学年人教版八年级数学下册17.1勾股定理同步练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册17.1勾股定理同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 436.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 12:54:55 | ||
图片预览


文档简介
10756900106807001144270011404600 第十七章勾股定理 17.1 勾股定理 同步练习
一、选择题
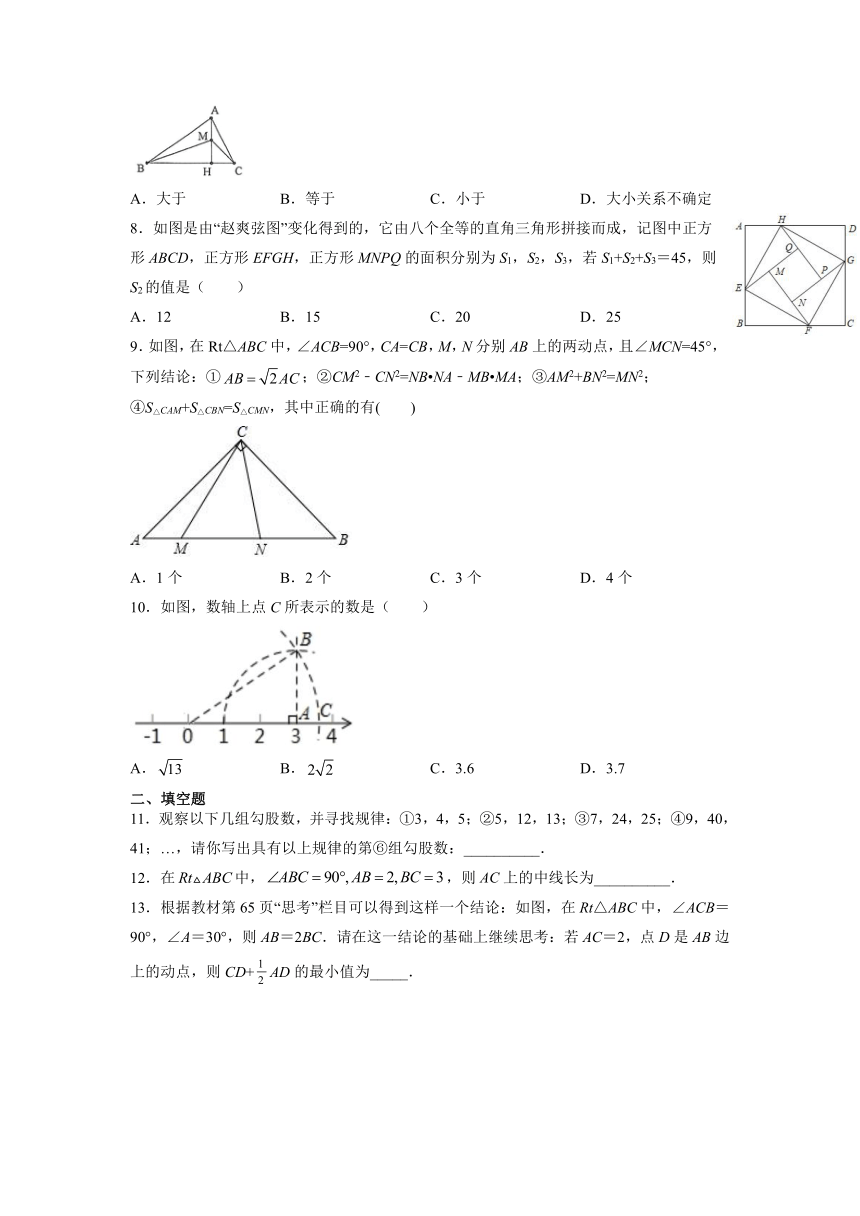
1.下列各组数中不是勾股数的是( )
A.3,4.5 B.6.8.10 C.5,12.13 D.4,5,6
2.已知直角三角形两边的长为3和4,则此三角形的周长为( ).
A.12 B.7+ C.12或7+ D.以上都不对
3.如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
A. B.﹣ C. D.﹣
4.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
5.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=3,BD是△ABC的中线,过点C作CP⊥BD于点P,图中阴影部分的面积为( )
A. B. C. D.
6.如图,一张直角三角形纸片,两直角边AC=4cm,BC=8cm,将△ABC折叠,点B与点A重合,折痕为DE,则DE的长为( ).
A. B. C. D.5
7.如图,在中,,于H,M为AH上异于A的一点,比较与的大小,则( ).
5895975220980A.大于 B.等于 C.小于 D.大小关系不确定
8.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12 B.15 C.20 D.25
9.如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①;②CM2﹣CN2=NB?NA﹣MB?MA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,数轴上点C所表示的数是( )
A. B. C.3.6 D.3.7
二、填空题
11.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
12.在中,,则上的中线长为__________.
13.根据教材第65页“思考”栏目可以得到这样一个结论:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB边上的动点,则CD+AD的最小值为_____.
14.在Rt△ABC中,∠C=90°,AC=6,点D为边BC上一点,将△ACD沿直线AD翻折得到△AED,点C的对应点为点E,联结BE,如果△BDE是以BD为直角边的等腰直角三角形,那么BC的长等于______.
15.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了__米.
三、解答题
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
19.如图,在直角坐标系中,三角形两顶点的坐标为,点是轴上一动点(不与点重合),过点作,分别平分.
当点在点左边,三角形的面积为时,求点的坐标;
当轴时,求的度数.
20.在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.
(1)求AB的长;
(2)如图,点P从点B出发,以每秒2cm的速度沿B→A→C运动,运动到点C时停止,设运动时间为t秒.
①若△PBC的面积为36cm2,求t的值;
②若将△ABC沿经过点 C、P的直线折叠,点B恰好落在边AC上,则t= .
21.若图是一个高为3米,长为5米的楼梯表面铺地毯.
(1)求地毯的长是多少米?
(2)如果地毯的宽是2米,地毯每平方售价是10元,铺这个楼梯一共需要多少元?
22.如图,某测量员测量公园内一棵树的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为.已知A点的高度为3米,台阶的坡度为(即),且B、C、E三点在同一条直线上.
(1)求斜坡的长;
(2)请根据以上条件求出树的高度.(侧倾器的高度忽略不计)
23.阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(,),P2(,)其两点间的距离P1P2 = ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为| ? |或| ? |.
(1)已知 A (1,4)、B (-3,2),试求 A、B两点间的距离;
(2)已知一个三角形各顶点坐标为 D(-1,4)、E(-2,2)、F(3,2),你能判定此三角形的形状吗?说明理由:
(3)在(2)的条件下,平面直角坐标系中,在 x轴上找一点 P,使得?PDF是以DF为底的等腰三角形,求点P的坐标.
【参考答案】
1.D 2.C 3.D 4.C 5.C 6.B 7.C 8.B 9.C 10.A
11.13,84,85
12.
13.
14.12或
15.9.
16.(1),
∵,,
∴.
故答案为:c-a,d-b.
(2)如图,过点B作BE⊥AC于E.
则|BE|=|CD|=c-a,|AE|=|DB|-|CA|=d-b
在Rt△ABE中,由勾股定理得:.
故答案为:
(3)由(2)得:,
所以.
17.解:(1)根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2;
(2)证明:∵(2mn)2+(m2﹣n2)2=4m2n2+m4﹣2m2n2+n4=m4+2m2n2+n4=(m2+n2)2,
∵m、n是正整数且m>n,
∴2mn、m2﹣n2、m2+n2是勾股数.
18.(1)解:当出发2秒后,AP=2,BQ=4,
∴BP=AB-AP=8-2=6,
∵∠B=90°,
∴(cm)
(2)解:∵BQ=2t,BC=6,
∴CQ=6-2t,
∴,
得t=2;
(3)解:在中,,
∴10,
当点Q在AC上时,,
∵BC=6,BP=8-t,
∴PQ分△ABC的周长中BP+BC+CQ=,AP+AQ=,
当时,得t=4;
当时,得t=6;
检验可得t值均符合题意,
∴t为4或6时,将周长分为23:25两部分.
19.(1) (2)45°
20.(1)cm;(2)①或;②
21.(1)7米;(2)140元
22.(1)米;(2)树高为9米.
23.(1) ;(2)是直角三角形;(3)
一、选择题
1.下列各组数中不是勾股数的是( )
A.3,4.5 B.6.8.10 C.5,12.13 D.4,5,6
2.已知直角三角形两边的长为3和4,则此三角形的周长为( ).
A.12 B.7+ C.12或7+ D.以上都不对
3.如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
A. B.﹣ C. D.﹣
4.如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
A.5 B.6 C.8 D.10
5.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=3,BD是△ABC的中线,过点C作CP⊥BD于点P,图中阴影部分的面积为( )
A. B. C. D.
6.如图,一张直角三角形纸片,两直角边AC=4cm,BC=8cm,将△ABC折叠,点B与点A重合,折痕为DE,则DE的长为( ).
A. B. C. D.5
7.如图,在中,,于H,M为AH上异于A的一点,比较与的大小,则( ).
5895975220980A.大于 B.等于 C.小于 D.大小关系不确定
8.如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNPQ的面积分别为S1,S2,S3,若S1+S2+S3=45,则S2的值是( )
A.12 B.15 C.20 D.25
9.如图,在Rt△ABC中,∠ACB=90°,CA=CB,M,N分别AB上的两动点,且∠MCN=45°,下列结论:①;②CM2﹣CN2=NB?NA﹣MB?MA;③AM2+BN2=MN2;④S△CAM+S△CBN=S△CMN,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,数轴上点C所表示的数是( )
A. B. C.3.6 D.3.7
二、填空题
11.观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…,请你写出具有以上规律的第⑥组勾股数:__________.
12.在中,,则上的中线长为__________.
13.根据教材第65页“思考”栏目可以得到这样一个结论:如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB边上的动点,则CD+AD的最小值为_____.
14.在Rt△ABC中,∠C=90°,AC=6,点D为边BC上一点,将△ACD沿直线AD翻折得到△AED,点C的对应点为点E,联结BE,如果△BDE是以BD为直角边的等腰直角三角形,那么BC的长等于______.
15.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了__米.
三、解答题
16.某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱,绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
17.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛)一尺,不合四寸,问门广几何?其大意:如图,推开双门(大小相同),双门间隙CD=4寸,点C、点D与门槛AB的距离CE=DF=1尺(1尺=10寸),求AB的长.
18.如图所示,折叠长方形的一边,使点落在边的点处,已知,,求的长.
19.如图,在直角坐标系中,三角形两顶点的坐标为,点是轴上一动点(不与点重合),过点作,分别平分.
当点在点左边,三角形的面积为时,求点的坐标;
当轴时,求的度数.
20.在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.
(1)求AB的长;
(2)如图,点P从点B出发,以每秒2cm的速度沿B→A→C运动,运动到点C时停止,设运动时间为t秒.
①若△PBC的面积为36cm2,求t的值;
②若将△ABC沿经过点 C、P的直线折叠,点B恰好落在边AC上,则t= .
21.若图是一个高为3米,长为5米的楼梯表面铺地毯.
(1)求地毯的长是多少米?
(2)如果地毯的宽是2米,地毯每平方售价是10元,铺这个楼梯一共需要多少元?
22.如图,某测量员测量公园内一棵树的高度,他们在这棵树左侧一斜坡上端点A处测得树顶端D的仰角为,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为.已知A点的高度为3米,台阶的坡度为(即),且B、C、E三点在同一条直线上.
(1)求斜坡的长;
(2)请根据以上条件求出树的高度.(侧倾器的高度忽略不计)
23.阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1(,),P2(,)其两点间的距离P1P2 = ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为| ? |或| ? |.
(1)已知 A (1,4)、B (-3,2),试求 A、B两点间的距离;
(2)已知一个三角形各顶点坐标为 D(-1,4)、E(-2,2)、F(3,2),你能判定此三角形的形状吗?说明理由:
(3)在(2)的条件下,平面直角坐标系中,在 x轴上找一点 P,使得?PDF是以DF为底的等腰三角形,求点P的坐标.
【参考答案】
1.D 2.C 3.D 4.C 5.C 6.B 7.C 8.B 9.C 10.A
11.13,84,85
12.
13.
14.12或
15.9.
16.(1),
∵,,
∴.
故答案为:c-a,d-b.
(2)如图,过点B作BE⊥AC于E.
则|BE|=|CD|=c-a,|AE|=|DB|-|CA|=d-b
在Rt△ABE中,由勾股定理得:.
故答案为:
(3)由(2)得:,
所以.
17.解:(1)根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
∴(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2;
(2)证明:∵(2mn)2+(m2﹣n2)2=4m2n2+m4﹣2m2n2+n4=m4+2m2n2+n4=(m2+n2)2,
∵m、n是正整数且m>n,
∴2mn、m2﹣n2、m2+n2是勾股数.
18.(1)解:当出发2秒后,AP=2,BQ=4,
∴BP=AB-AP=8-2=6,
∵∠B=90°,
∴(cm)
(2)解:∵BQ=2t,BC=6,
∴CQ=6-2t,
∴,
得t=2;
(3)解:在中,,
∴10,
当点Q在AC上时,,
∵BC=6,BP=8-t,
∴PQ分△ABC的周长中BP+BC+CQ=,AP+AQ=,
当时,得t=4;
当时,得t=6;
检验可得t值均符合题意,
∴t为4或6时,将周长分为23:25两部分.
19.(1) (2)45°
20.(1)cm;(2)①或;②
21.(1)7米;(2)140元
22.(1)米;(2)树高为9米.
23.(1) ;(2)是直角三角形;(3)
