2021--2022学年人教版八年级数学下册17.1勾股定理提高练习(Word版含答案)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册17.1勾股定理提高练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 306.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 12:54:52 | ||
图片预览


文档简介
17.1勾股定理提高练习
一、单选题
1.下列几组数中,是勾股数的一组是( )
A.1.5,2,3.5 B.21,45,51
C.一3,-4,-5 D.8,15,17
2.在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.c2﹣a2=b2
3.如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
A. B. C. D.
4.如图所示,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,他们同时出发,一个半小时后,甲、乙两渔船相距( )
A.12海里 B.13海里 C.14海里 D.15海里
5.放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是50米/分,红红用12分钟到家,晓晓用16分钟到家,红红家和晓晓家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
6.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A.1 B. C. D.2
7.如图,线段AB=、CD=,那么,线段EF的长度为( )
A. B. C. D.
8.在△ABC中,AB=10,AC=2,BC边上的高AD=6,则另一边BC等于( )
A.10 B.8 C.6或10 D.8或10
9.如图,在矩形中,,,点是边上一点,将沿折叠,使点落在点处.连结,当为直角三角形时,的长是( )
A. B. C.或 D.或
10.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
二、填空题
11.下列命题:①如果直角三角形的三边是a、b、c,那么;②一个等腰直角三角形的三边是a、b、c(a>b=c),那么;③如果三条线段a、b、c满足,那么以这三条线段组成的三角形是直角三角形;④如果a、b、c为一组勾股数,那么4a、4b、4c仍是一组勾股数.其中是真命题的是______.
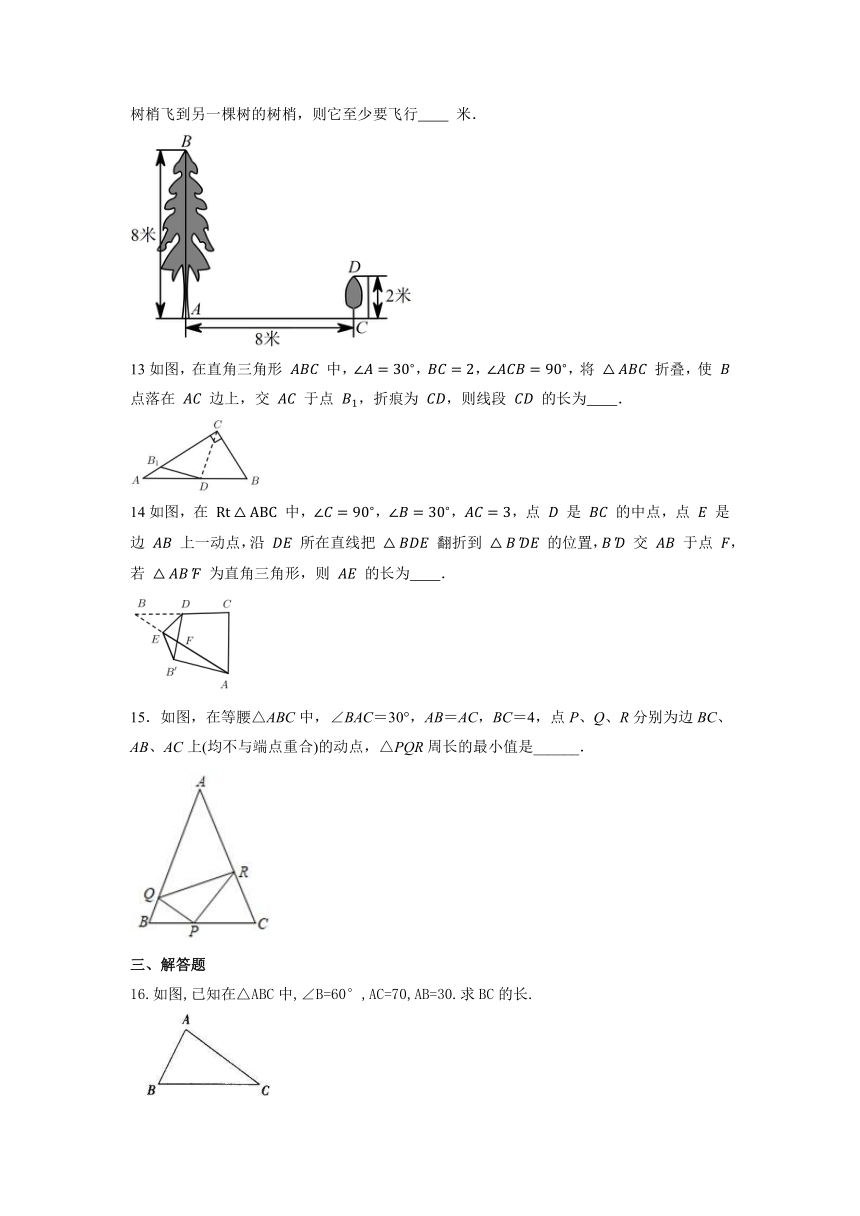
12如图,有两棵树,一棵高 米,另一棵高 米,两树相距 米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行 米.
13如图,在直角三角形 中,,,,将 折叠,使 点落在 边上,交 于点 ,折痕为 ,则线段 的长为 .
14如图,在 中,,,,点 是 的中点,点 是边 上一动点,沿 所在直线把 翻折到 的位置, 交 于点 ,若 为直角三角形,则 的长为 .
15.如图,在等腰△ABC中,∠BAC=30°,AB=AC,BC=4,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,△PQR周长的最小值是______.
三、解答题
16.如图,已知在△ABC中,∠B=60°,AC=70,AB=30.求BC的长.
17.如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
18.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
19.定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是5,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,直角边长为,,斜边为c,求::的值;
(3)如图,ABC中,BC=2,CD为ABC的中线,且CD=AB.若是平方倍三角形,求ABC的面积.
参考答案:
1.D 2.C 3.A 4.D 5.C 6.D 7.C 8.C 9.D 10.B
11.②③④
12.
13.
14. 或
15.##
16.解:作于D,则因,
∴(的两个锐角互余)
∴
根据勾股定理,在中,.
根据勾股定理,在中,.
∴ .
17.解:∵AD⊥BC,∠C=45°,
∴△ACD是等腰直角三角形,
∵AD=CD.
∵AC=2,
∴2AD2=AC2,即2AD2=8,
解得:AD=CD=2.
∵∠B=30°,∴AB=2AD=4,
∴BD===2,
∴BC=BD+CD=2+2,
∴S△ABC=BC AD=(2+2)×2=2+2.
18.解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,
∴4=,12=,24=…
∴11,60,61;13,84,85;
(2)后两个数表示为和,
∵a2+()2=a2+==,
=,∴a2+()2=,
又∵a≥3,且a为奇数,∴由a,,三个数组成的数是勾股数.
19.(1)
解:结论:这个三角形是“平方倍三角形”.理由如下:
∵,,
∴,
∴这个三角形是“平方倍三角形”.
(2)
解:∵三角形为直角三角形,且直角边长为a和b,斜边为c,
∴由勾股定理可知:,
∵三角形是平方倍三角形,
∴或者,
当时:由①、②两式得到:,
整理得到:,即:,
再代入①中得到:,
∴;
当时:由①、③两式得到:,
整理得到:,即:,
再代入①中得到:,
∴;
综上所述:.
(3)
解:如下图所示:
∵CD为ABC的中线,
∴AD=BD=AB,
由已知CD=AB,
∴AD=CD=BD,
∴∠DAC=∠DCA,∠DCB=∠DBC,
又△ABC内角和为180°,
∴∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴2∠DCA+2∠DCB=180°,
∴∠DCA+∠DCB=90°,即∠ACB=90°,
∴△ABC为直角三角形,
由已知条件是平方倍三角形可知:
设AD=CD=DB=x(x>0),
情况一:当AD +CD =3AC 时:得到3AC =2x ,
∴,
在Rt△ABC中,由勾股定理可知:AC +BC =AB ,代入数据:
,解出(负值舍去),
∴,
∴;
情况二:当AD +AC =3CD 时:得到AC =2x ,
∴在Rt△ABC中,由勾股定理可知:AC +BC =AB ,代入数据:
,解出(负值舍去),
∴,
∴;
综上所述:△ABC的面积为或.
一、单选题
1.下列几组数中,是勾股数的一组是( )
A.1.5,2,3.5 B.21,45,51
C.一3,-4,-5 D.8,15,17
2.在△ABC中,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )
A.a2+b2=c2 B.b2+c2=a2 C.a2+c2=b2 D.c2﹣a2=b2
3.如图,在高为,坡面长为的楼梯表面铺地毯,地毯的长度至少需要( )
A. B. C. D.
4.如图所示,甲渔船以8海里/时的速度离开港口O向东北方向航行,乙渔船以6海里/时的速度离开港口O向西北方向航行,他们同时出发,一个半小时后,甲、乙两渔船相距( )
A.12海里 B.13海里 C.14海里 D.15海里
5.放学以后,红红和晓晓从学校分手,分别沿东南方向和西南方向回家,若红红和晓晓行走的速度都是50米/分,红红用12分钟到家,晓晓用16分钟到家,红红家和晓晓家的直线距离为( )
A.600米 B.800米 C.1000米 D.不能确定
6.如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A.1 B. C. D.2
7.如图,线段AB=、CD=,那么,线段EF的长度为( )
A. B. C. D.
8.在△ABC中,AB=10,AC=2,BC边上的高AD=6,则另一边BC等于( )
A.10 B.8 C.6或10 D.8或10
9.如图,在矩形中,,,点是边上一点,将沿折叠,使点落在点处.连结,当为直角三角形时,的长是( )
A. B. C.或 D.或
10.如图,一艘船以40km/h的速度沿既定航线由西向东航行,途中接到台风警报,某台风中心正以20km/h的速度由南向北移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离BA=300km,如果这艘轮船会受到台风影响,那么从接到警报开始,经过( )小时它就会进入台风影响区
A.10 B.7 C.6 D.12
二、填空题
11.下列命题:①如果直角三角形的三边是a、b、c,那么;②一个等腰直角三角形的三边是a、b、c(a>b=c),那么;③如果三条线段a、b、c满足,那么以这三条线段组成的三角形是直角三角形;④如果a、b、c为一组勾股数,那么4a、4b、4c仍是一组勾股数.其中是真命题的是______.
12如图,有两棵树,一棵高 米,另一棵高 米,两树相距 米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行 米.
13如图,在直角三角形 中,,,,将 折叠,使 点落在 边上,交 于点 ,折痕为 ,则线段 的长为 .
14如图,在 中,,,,点 是 的中点,点 是边 上一动点,沿 所在直线把 翻折到 的位置, 交 于点 ,若 为直角三角形,则 的长为 .
15.如图,在等腰△ABC中,∠BAC=30°,AB=AC,BC=4,点P、Q、R分别为边BC、AB、AC上(均不与端点重合)的动点,△PQR周长的最小值是______.
三、解答题
16.如图,已知在△ABC中,∠B=60°,AC=70,AB=30.求BC的长.
17.如图,在△ABC中,∠B=30°,∠C=45°,AC=2.求BC边上的高及△ABC的面积.
18.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
19.定义:若一个三角形存在两边平方和等于第三边平方的3倍,则称此三角形为“平方倍三角形”.
(1)若一个三角形的三边长分别是5,和2,这个三角形是否为平方倍三角形?请你作出判断并说明理由;
(2)若一个直角三角形是平方倍三角形,直角边长为,,斜边为c,求::的值;
(3)如图,ABC中,BC=2,CD为ABC的中线,且CD=AB.若是平方倍三角形,求ABC的面积.
参考答案:
1.D 2.C 3.A 4.D 5.C 6.D 7.C 8.C 9.D 10.B
11.②③④
12.
13.
14. 或
15.##
16.解:作于D,则因,
∴(的两个锐角互余)
∴
根据勾股定理,在中,.
根据勾股定理,在中,.
∴ .
17.解:∵AD⊥BC,∠C=45°,
∴△ACD是等腰直角三角形,
∵AD=CD.
∵AC=2,
∴2AD2=AC2,即2AD2=8,
解得:AD=CD=2.
∵∠B=30°,∴AB=2AD=4,
∴BD===2,
∴BC=BD+CD=2+2,
∴S△ABC=BC AD=(2+2)×2=2+2.
18.解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,
∴4=,12=,24=…
∴11,60,61;13,84,85;
(2)后两个数表示为和,
∵a2+()2=a2+==,
=,∴a2+()2=,
又∵a≥3,且a为奇数,∴由a,,三个数组成的数是勾股数.
19.(1)
解:结论:这个三角形是“平方倍三角形”.理由如下:
∵,,
∴,
∴这个三角形是“平方倍三角形”.
(2)
解:∵三角形为直角三角形,且直角边长为a和b,斜边为c,
∴由勾股定理可知:,
∵三角形是平方倍三角形,
∴或者,
当时:由①、②两式得到:,
整理得到:,即:,
再代入①中得到:,
∴;
当时:由①、③两式得到:,
整理得到:,即:,
再代入①中得到:,
∴;
综上所述:.
(3)
解:如下图所示:
∵CD为ABC的中线,
∴AD=BD=AB,
由已知CD=AB,
∴AD=CD=BD,
∴∠DAC=∠DCA,∠DCB=∠DBC,
又△ABC内角和为180°,
∴∠DAC+∠DCA+∠DCB+∠DBC=180°,
∴2∠DCA+2∠DCB=180°,
∴∠DCA+∠DCB=90°,即∠ACB=90°,
∴△ABC为直角三角形,
由已知条件是平方倍三角形可知:
设AD=CD=DB=x(x>0),
情况一:当AD +CD =3AC 时:得到3AC =2x ,
∴,
在Rt△ABC中,由勾股定理可知:AC +BC =AB ,代入数据:
,解出(负值舍去),
∴,
∴;
情况二:当AD +AC =3CD 时:得到AC =2x ,
∴在Rt△ABC中,由勾股定理可知:AC +BC =AB ,代入数据:
,解出(负值舍去),
∴,
∴;
综上所述:△ABC的面积为或.
