2021—2022学年人教版七年级数学下册5.3.1平行线的性质课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版七年级数学下册5.3.1平行线的性质课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 543.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 12:56:55 | ||
图片预览



文档简介
5.3.1平行线的性质
一、选择题
1.把直线a沿水平方向平移4cm,平移后的线为直线b,则直线a与直线b之间的距离为( )
A.等于4cm B.小于4cm C.大于4cm D.不大于4cm
2.如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
3.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
.62° B.58° C.52° D.48°
第2题图 第3题图 第4题图
4.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
5.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20° B.55° C.20°或125° D.20°或55°
6.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
7.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是( )
A.∠BAO与∠CAO相等 B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余 D.∠ABO与∠DBO不等
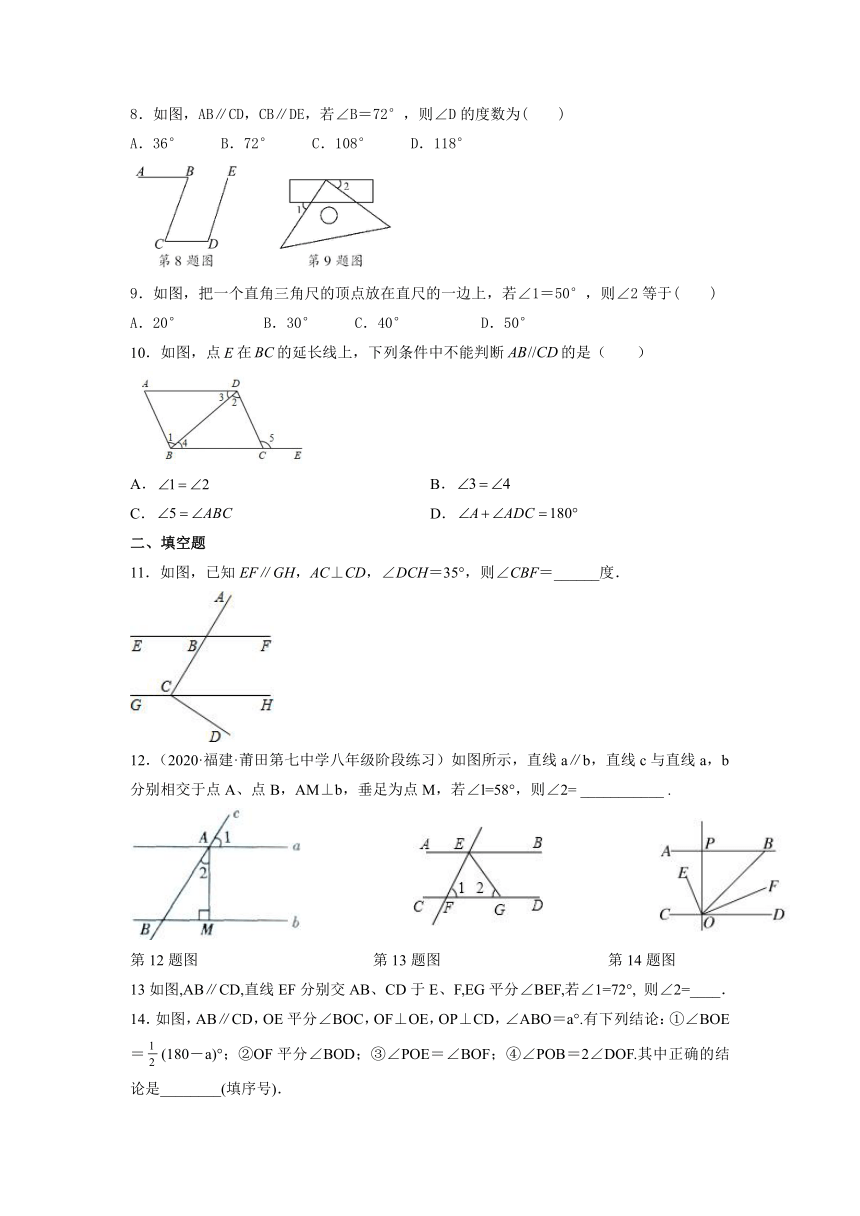
8.如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
A.36° B.72° C.108° D.118°
9.如图,把一个直角三角尺的顶点放在直尺的一边上,若∠1=50°,则∠2等于( )
A.20° B.30° C.40° D.50°
10.如图,点在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
二、填空题
11.如图,已知EF∥GH,AC⊥CD,∠DCH=35°,则∠CBF=______度.
12.(2020·福建·莆田第七中学八年级阶段练习)如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2= ___________ .
4343400876302495550158115
第12题图 第13题图 第14题图
13如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=____.
14.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.如图,已知ABCD,BE平分∠ABC,DE平分∠ADC,若∠ABC =m°,∠ADC =n°,则∠E=_________°.
三、解答题
16.如图,在中,平分交于D,平分交于F,已知,求证:.
17.已知:如图,直线,直线MN交EF,PO于点A,B,直线HQ交EF,PO于点D,C,DG与OP交于点G,若,,.
(1)求证:;
(2)请直接写出的度数.
18.如图,AB∥CD,E是CD上一点,AE交BC于点F,且∠ABE=∠DBC,∠ABC=∠AEB.
(1)试判断AE与BD的位置关系,并说明理由;
(2)若BE平分∠CBD,∠AEB=40°,求∠D的度数.
19.如图,,.
(1)求证;
(2)若平分,于点,,求的度数.
20.如图,点,分别在的边,上,点在线段上,且,.
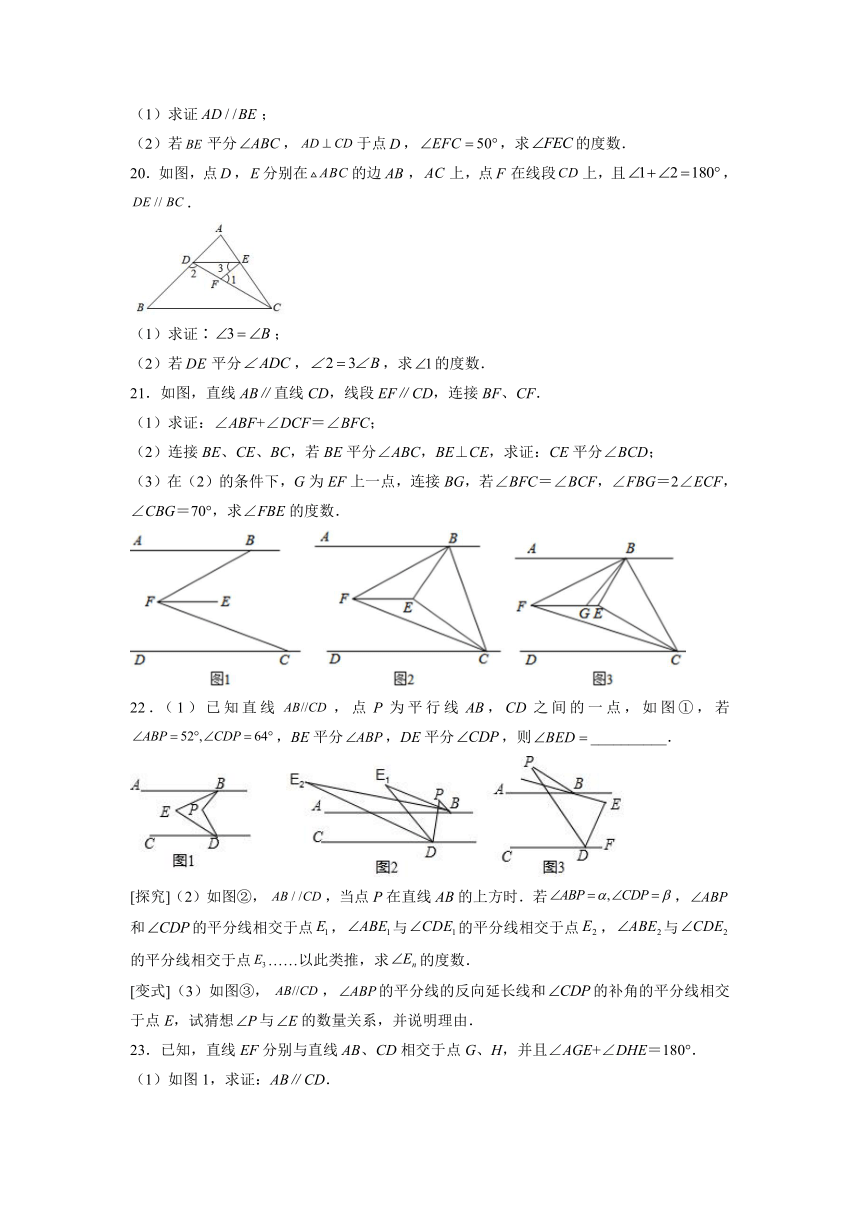
(1)求证∶;
(2)若平分,,求的度数.
21.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;
(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;
(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
22.(1)已知直线,点P为平行线AB,CD之间的一点,如图①,若,BE平分,DE平分,则__________.
[探究](2)如图②,,当点P在直线AB的上方时.若,和的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,求的度数.
[变式](3)如图③,,的平分线的反向延长线和的补角的平分线相交于点E,试猜想与的数量关系,并说明理由.
23.已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
【参考答案】
1.D 2.A 3.A 4.D 5.C 6.B 7.D 8.C 9.C 10.B
11.125
12.32°【详解】
∵直线a∥b,AM⊥b,
∴AM⊥a;
∴∠2=180°-90°-∠1;
∵∠1=58°,
∴∠2=32°.
故答案是:32°.
13.54°【详解】
∵AB∥CD,
∴∠BEF=180°?∠1=180°?72°=108°
∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°
∴∠2=∠BEG=54°.
故答案为54°.
14.①②③【详解】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15.
16.证明:(已知),
(同位角相等,两直线平行),
(两直线平行,同位角相等),
平分,平分(已知),
,(角平分线的定义),
(等量代换).
(同位角相等,两直线平行).
17.解:(1)∵,
∴,
∵,
∴,
∴;
(2)∵,,
∴,
,
∵,
∴,
∴.
18.(1),理由如下,
∠ABE=∠DBC,
即,
,
∠ABC=∠AEB,
,
,
(2)BE平分∠CBD,∠AEB=40°,
,
,
,
,
AB∥CD,
.
19.(1)证明:,
.
,
,
,
;
(2)解:.
又平分,
,
,
,
,
,
,
.
20.解:(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)∵平分,
∴,
∵,
∴,
∵,,
∴.
∴.
∵,
∴.
21.证明:(1)∵AB∥CD,EF∥CD,
∴AB∥EF,
∴∠ABF=∠BFE,
∵EF∥CD,
∴∠DCF=∠EFC,
∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,
∴∠BEC=90°,
∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,
∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ECD=∠BCE,
∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,
∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,
∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,
∴∠BFC=∠BCE+∠ECF=γ+β,
∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,
∴∠FBG=2γ,
∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,
∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,
∴∠CBE=∠ABE=90°﹣β,
∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,
整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
22.解:(1)如图1,过作,而,
,
,,
,
又,,平分,平分,
,,
,
故答案为:;
(2)如图2,和的平分线交于点,
,,
,
,
,
与的角平分线交于点,
,,
,
,
,
同理可得,,
以此类推,的度数为.
(3).理由如下:
如图3,过作,而,
,
,,
,
又的角平分线的反向延长线和的补角的角平分线交于点,
,,
,
,
,
.
23.证明:(1)由对顶角相等得:,
,
,
;
(2)如图,过点作,
,
由(1)已证:,
,
,
;
(3)不变,求解过程如下:
由(2)可知,,
,即,
,即,
如图,延长交于点,
,
,
,
,
,
是的平分线,是的平分线,
,
,
一、选择题
1.把直线a沿水平方向平移4cm,平移后的线为直线b,则直线a与直线b之间的距离为( )
A.等于4cm B.小于4cm C.大于4cm D.不大于4cm
2.如图,直线a∥b,直线AB⊥AC,若∠1=52°,则∠2的度数是( )
A.38° B.42° C.48° D.52°
3.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
.62° B.58° C.52° D.48°
第2题图 第3题图 第4题图
4.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于( )
A.112° B.110° C.108° D.106°
5.在同一平面内,若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠A的度数为( )
A.20° B.55° C.20°或125° D.20°或55°
6.如图所示,AB∥CD,若∠2=2∠1﹣6°,则∠2等于( )
A.116° B.118° C.120° D.124°
7.如图,直线AC∥BD,AO,BO分别是∠BAC,∠ABD的平分线,那么下列结论错误的是( )
A.∠BAO与∠CAO相等 B.∠BAC与∠ABD互补
C.∠BAO与∠ABO互余 D.∠ABO与∠DBO不等
8.如图,AB∥CD,CB∥DE,若∠B=72°,则∠D的度数为( )
A.36° B.72° C.108° D.118°
9.如图,把一个直角三角尺的顶点放在直尺的一边上,若∠1=50°,则∠2等于( )
A.20° B.30° C.40° D.50°
10.如图,点在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
二、填空题
11.如图,已知EF∥GH,AC⊥CD,∠DCH=35°,则∠CBF=______度.
12.(2020·福建·莆田第七中学八年级阶段练习)如图所示,直线a∥b,直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠l=58°,则∠2= ___________ .
4343400876302495550158115
第12题图 第13题图 第14题图
13如图,AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2=____.
14.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是________(填序号).
15.如图,已知ABCD,BE平分∠ABC,DE平分∠ADC,若∠ABC =m°,∠ADC =n°,则∠E=_________°.
三、解答题
16.如图,在中,平分交于D,平分交于F,已知,求证:.
17.已知:如图,直线,直线MN交EF,PO于点A,B,直线HQ交EF,PO于点D,C,DG与OP交于点G,若,,.
(1)求证:;
(2)请直接写出的度数.
18.如图,AB∥CD,E是CD上一点,AE交BC于点F,且∠ABE=∠DBC,∠ABC=∠AEB.
(1)试判断AE与BD的位置关系,并说明理由;
(2)若BE平分∠CBD,∠AEB=40°,求∠D的度数.
19.如图,,.
(1)求证;
(2)若平分,于点,,求的度数.
20.如图,点,分别在的边,上,点在线段上,且,.
(1)求证∶;
(2)若平分,,求的度数.
21.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;
(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;
(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
22.(1)已知直线,点P为平行线AB,CD之间的一点,如图①,若,BE平分,DE平分,则__________.
[探究](2)如图②,,当点P在直线AB的上方时.若,和的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,求的度数.
[变式](3)如图③,,的平分线的反向延长线和的补角的平分线相交于点E,试猜想与的数量关系,并说明理由.
23.已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.
(1)如图1,求证:AB∥CD.
(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.
(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD的平分线,作HN∥PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)
【参考答案】
1.D 2.A 3.A 4.D 5.C 6.B 7.D 8.C 9.C 10.B
11.125
12.32°【详解】
∵直线a∥b,AM⊥b,
∴AM⊥a;
∴∠2=180°-90°-∠1;
∵∠1=58°,
∴∠2=32°.
故答案是:32°.
13.54°【详解】
∵AB∥CD,
∴∠BEF=180°?∠1=180°?72°=108°
∠2=∠BEG,
又∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°
∴∠2=∠BEG=54°.
故答案为54°.
14.①②③【详解】
①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF; 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
15.
16.证明:(已知),
(同位角相等,两直线平行),
(两直线平行,同位角相等),
平分,平分(已知),
,(角平分线的定义),
(等量代换).
(同位角相等,两直线平行).
17.解:(1)∵,
∴,
∵,
∴,
∴;
(2)∵,,
∴,
,
∵,
∴,
∴.
18.(1),理由如下,
∠ABE=∠DBC,
即,
,
∠ABC=∠AEB,
,
,
(2)BE平分∠CBD,∠AEB=40°,
,
,
,
,
AB∥CD,
.
19.(1)证明:,
.
,
,
,
;
(2)解:.
又平分,
,
,
,
,
,
,
.
20.解:(1)证明:∵,,
∴,
∴,
∴,
∵,
∴,
∴;
(2)∵平分,
∴,
∵,
∴,
∵,,
∴.
∴.
∵,
∴.
21.证明:(1)∵AB∥CD,EF∥CD,
∴AB∥EF,
∴∠ABF=∠BFE,
∵EF∥CD,
∴∠DCF=∠EFC,
∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,
∴∠BEC=90°,
∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,
∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ECD=∠BCE,
∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,
∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,
∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,
∴∠BFC=∠BCE+∠ECF=γ+β,
∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,
∴∠FBG=2γ,
∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,
∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,
∴∠CBE=∠ABE=90°﹣β,
∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,
整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
22.解:(1)如图1,过作,而,
,
,,
,
又,,平分,平分,
,,
,
故答案为:;
(2)如图2,和的平分线交于点,
,,
,
,
,
与的角平分线交于点,
,,
,
,
,
同理可得,,
以此类推,的度数为.
(3).理由如下:
如图3,过作,而,
,
,,
,
又的角平分线的反向延长线和的补角的角平分线交于点,
,,
,
,
,
.
23.证明:(1)由对顶角相等得:,
,
,
;
(2)如图,过点作,
,
由(1)已证:,
,
,
;
(3)不变,求解过程如下:
由(2)可知,,
,即,
,即,
如图,延长交于点,
,
,
,
,
,
是的平分线,是的平分线,
,
,
