探索勾股定理说课

课件31张PPT。探索勾股定理一、教材分析（1）教材的地位和作用
（2） 教学目标
（一）教材的地位和作用 “探索勾股定理”是义务教育课程标准实验教科书八年级（下册）第十八章第一节内容《勾股定理》的第1课时。“勾股定理”是安排在学生学习了三角形、全等三角形、等腰三角形等有关知识之后，它揭示了直角三角形三边之间的一种美妙关系，将形与数密切联系起来，在几何学中占有非常重要的位置。同时，勾股定理在生产、生活中也有很大的用途。（二）教学目标
知识技能：了解勾股定理的文化背景，体验勾股定理的探索过程 。过程与方法：（1）通过拼图活动，体验数学思维的严谨性，发展形象思维。（2）在探究活动中，学会与人合作，并在与他人交流中获取探究结果。情感目标：（1）通过对勾股定理历史的了解，感受数学文化，激发学习热情。（2）在探究活动中，体验解决问题方法的多样性，培养学生的合作交流意识和探索精神。二、教学重点、难点重点：勾股定理的内容及其应用
难点：勾股定理的证明
突破难点的关键：“拼图法”和“面积法”的成功运用三、教法与学法分析：教法：以引导探索法为主，实验法、讨论法为辅，由浅到深，由特殊到一般。充分利用教具及多媒体等教学手段。
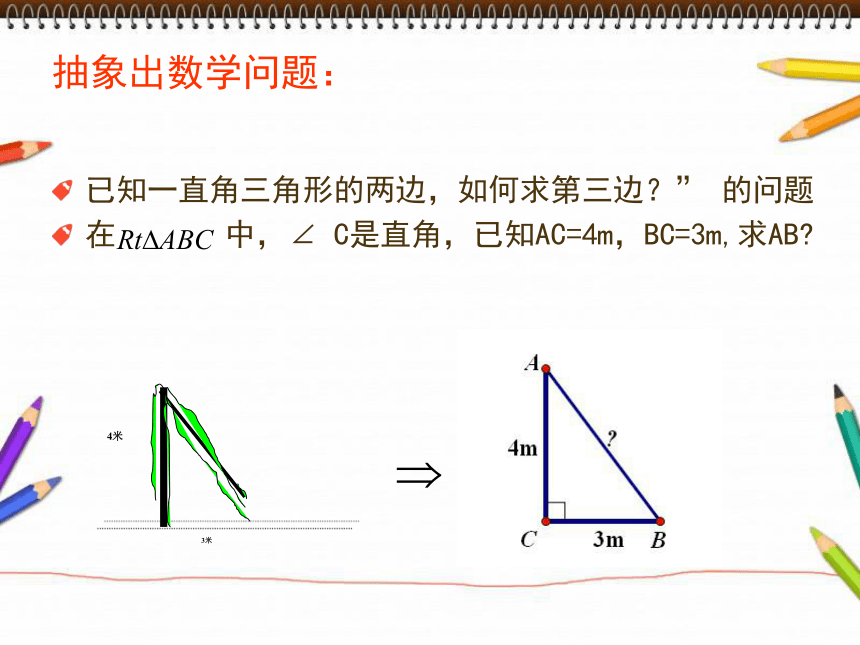
学法：引导学生动手操作，自主探索，合作交流。四、教学过程（5步骤）一、创设情境引入新课二、动手操作探索新知三、证明猜想得到定理四、应用知识，回归生活五、总结反思，布置作业（一）、创设情境，引入新课（2’）一棵树在离地面4米处断裂，树的顶部落在离
树跟底部3米处，求这棵树折断前有多高？ 抽象出数学问题：已知一直角三角形的两边，如何求第三边？” 的问题
在 中，∠ C是直角，已知AC=4m，BC=3m,求AB?　 相传2500年前，古希腊著名数学家毕达哥拉斯从朋友家的地砖铺成的地面上发现了直角三角形的某种特性，从而找到了答案。同学们,我们也来观察下面的地面, 看看你能发现什么？是否也和大数学家有同样的发现呢?【】请大家从面积的角度来观察图形： （二）、动手操作，探索新知 【活动1】 (1) 、在方格纸上,画一个顶点都在格点上的直角三角形;(2)、分别以这个直角三角形的各边为一边向三角形外作正方形；
(3)计算以各边为一边的正方形的面积.C如图，小方格的边长为1.(1)你能求出正方形R的面积吗？用了“补”的方法用了“割”的方法QacbSP+SQ=SR 观察所得到的各组数据，你有什么发现？猜想两直角边a、b与斜边c 之间的关系？a2+b2=c2acbSP+SQ=SR 观察所得到的各组数据，你有什么发现？（2）猜想:两直角边a、b与斜边c 之间的关系？a2+b2=c2 即：两条直角边上的正方形面积之和等于斜边上的正方形的面积（1）你能用三角形的边长表示正方形的面积吗？猜想：命题1 : 如果直角三角形的两直角边长
分别为a,b,斜边长为c，那么
拼一拼
以小组为单位用四个全等的直角三角形不加覆盖能拼成一个大正方形吗？abcabcabcabc（三）证明猜想，得到定理利用计算面积法：abcaaabbbccc┏acb 如果直角三角形的两直角边长分别为a和b，斜边长为c，那么 a2+b2=c2.勾股定理：【注】1、勾股定理的使用条件？
2、勾股定理可以用来解决什么问题？我国古代两种证法 1.“赵爽弦图”2.刘徽的“青朱出入图” 分享成果： 两千多年前，古希腊有个哥拉 斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派，1955勾 股 世 界国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前，国家之一。早在三千多年前 两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国外人们通常称勾股定理称为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票。 我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”，它被记载于我国古代著名的数学著作《周髀算经》中。分享成果：东西方思维方式及文化差异性赵爽弦图（中国）毕达哥拉斯树（古希腊）1.求下列直角三角形中未知边的长．y = 15x = 13z = 12（四）运用知识，解决问题。（15/）2.求下列图中表示边的未知数
x、y、z的值.xyz57662514416914481y = 5z = 7x = 225Y2+144=169（四）运用知识，回归生活3、解决导入时候提出的问题。前后呼应，学生从中体会到数学来源于生活同时又回归生活，为生活服务。树的高度=AC+AB。 例1 .在Rt△ABC中，∠Ｃ=90°.
(1) 已知：a=6，ｂ=8，求c；　
(2) 已知：a=40，c=41，求b；
(3) 已知: a:b=3:4, c=15,求a、b.例题分析(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立方程.
（五）归纳小结，布置作业【总结】1、直角三角形三边有何数量关系？2、勾股定理主要用于解决什么问题？
【反思】本节课的学习你参与了讨论了吗？新知识的学习你检测的结果如何？
【作业】1、课本P70 2、3、7
思考题：2、今有方尺一丈，葭生其中央。 出水一尺，引葭赴岸，适与岸齐，问：水深，葭长各几何？探索勾股定理板书设计勾股定理内容勾股定理的证明例题讲解习题训练1.根据学生的知识结构，我采用的教学流程是：创设情境导入新课—动手操作探究感 知—证明结论得到定理—应用知识回归生活—总结反思布置作业五部分，这一流程体现了知识发生、形成和发展的过程，让学生观察、猜想、归纳、验证的思想和数形结合的思想
2.从学生熟悉的生活事例，选择学生身边的、感兴趣的事物着手，体现了数学源于生活同时又回归于生活，服务于生活。
3.探索定理采用了面积法,引导学生利用实验由特殊到一般的对直角三角形三边关系的研究,得出结论.这种方法是认识事物规律重要方法之一,通过教学让学生初步掌握这种方法,对于学生良好思维品质的形成有重要作用,对学生的终身发展也有一定的作用。
五、设计说明：请各位老师指正谢谢观看