正余弦函数的单调性及其应用
图片预览





文档简介
课件14张PPT。正弦函数、余弦函数的单调性及其应用执教者:逊克县第一中学唐桂荣
1.起点目标:通过正弦、余弦函数的图像归纳其单调性
2.基础目标:会求简单三角函数的单调区间,
会利用单调性解决比较大小类别的题目;
3.提高目标:求复合函数的单调区间。
体会数形结合思想及整体换元思想
4.学习重点:由图像归纳正弦、余弦函数的单调区间
5.学习难点:复合函数单调性如何判断一个函数在某个区间具有单调性?
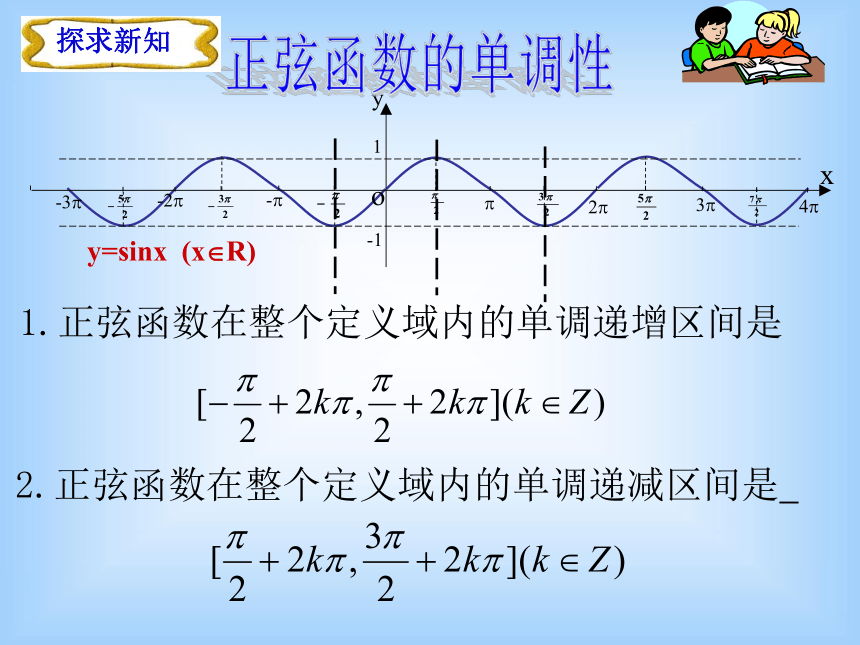
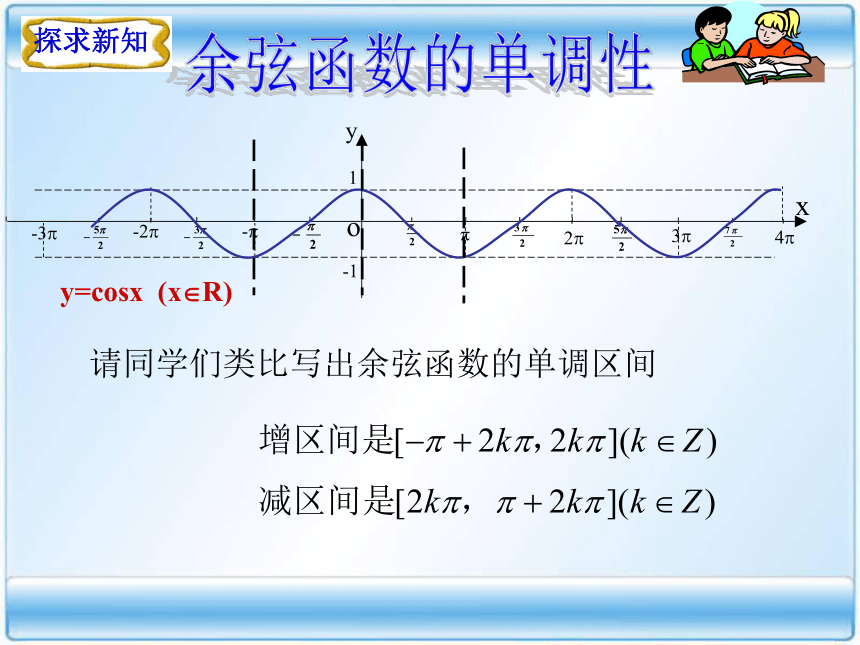
利用函数的单调性可以解决哪些问题? y=sinx (x?R)正弦函数的单调性1.正弦函数在整个定义域内的单调递增区间是 2.正弦函数在整个定义域内的单调递减区间是 y=cosx (x?R)余弦函数的单调性请同学们类比写出余弦函数的单调区间 方法:利用诱导公式将角转化到三角函数的同一个单调区间内,然后利用函数单调性即可比较大小。在同一单调区间内
还可以用三角函数线
比较函数值的大小。解:整体换元 <>B函数 的单调递减区间是 。 。注意:求复合函数的单调性,
当函数的定义域有限制时,
一定要先求出函数的定义域,
而所求单调区间一定是定义域的子集。这一节课你有哪些收获?1.正弦函数的单调递增区间单调递减区间2.余弦函数的单调递增区间[ +2k?, 2k?],k?Z单调递减区间(1). 利用单调性比较三角函数值的大小3.本节解决的两类题型(2).求简单三角函数和复合三角函数的单调区间-?
1、(A) 练习册双基达标
2、(B)练习册综合提高 祝同学们学习愉快,再见!
1.起点目标:通过正弦、余弦函数的图像归纳其单调性
2.基础目标:会求简单三角函数的单调区间,
会利用单调性解决比较大小类别的题目;
3.提高目标:求复合函数的单调区间。
体会数形结合思想及整体换元思想
4.学习重点:由图像归纳正弦、余弦函数的单调区间
5.学习难点:复合函数单调性如何判断一个函数在某个区间具有单调性?
利用函数的单调性可以解决哪些问题? y=sinx (x?R)正弦函数的单调性1.正弦函数在整个定义域内的单调递增区间是 2.正弦函数在整个定义域内的单调递减区间是 y=cosx (x?R)余弦函数的单调性请同学们类比写出余弦函数的单调区间 方法:利用诱导公式将角转化到三角函数的同一个单调区间内,然后利用函数单调性即可比较大小。在同一单调区间内
还可以用三角函数线
比较函数值的大小。解:整体换元 <>B函数 的单调递减区间是 。 。注意:求复合函数的单调性,
当函数的定义域有限制时,
一定要先求出函数的定义域,
而所求单调区间一定是定义域的子集。这一节课你有哪些收获?1.正弦函数的单调递增区间单调递减区间2.余弦函数的单调递增区间[ +2k?, 2k?],k?Z单调递减区间(1). 利用单调性比较三角函数值的大小3.本节解决的两类题型(2).求简单三角函数和复合三角函数的单调区间-?
1、(A) 练习册双基达标
2、(B)练习册综合提高 祝同学们学习愉快,再见!
