2021-2022学年人教版八年级数学下册17.1.2 勾股定理的应用 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1.2 勾股定理的应用 同步练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 17:15:08 | ||
图片预览



文档简介
17.1 勾股定理
第2课时 勾股定理的应用
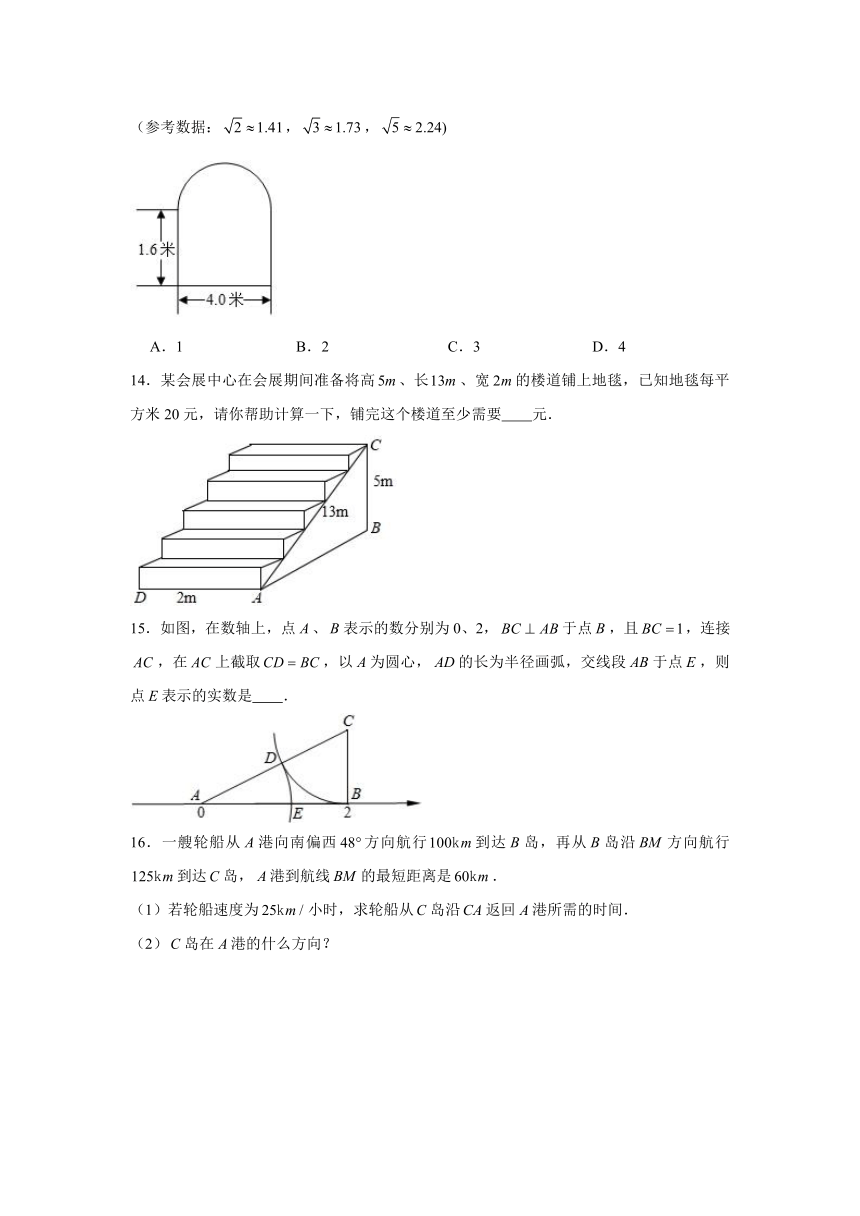
1.如图所示是某房屋顶框架的示意图,其中,,,,则的长度为
A. B. C. D.
2.一根旗杆在离地面3米处断裂,旗杆顶部落在离旗杆底部4米处,旗杆折断之前的高度是
A.5米 B.7米 C.8米 D.9米
3.如图,一架长的梯子靠在一竖直的墙上,这时梯子的底端到墙根的距离为,如果梯子的顶端下滑至,那么梯子底端将滑动
A. B. C. D.
4.如图,某自动感应门的正上方处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时米),感应门自动打开,则人头顶离感应器的距离等于
A.1.2米 B.1.5米 C.2.0米 D.2.5米
5.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙的距离为2寸,点和点距离门槛都为1尺尺寸),则的长是 寸.
6.如图数轴上的点表示的数是0,点表示的数是2,,垂足为,且,以为圆心,长为半径画弧,交数轴于点,则点表示的数为
A. B. C. D.
7.如图,在数轴上,点,对应的实数分别为1,3,,,以点为圆心,为半径画弧交数轴正半轴于点,则点对应的实数为
A. B. C. D.
8.如图,数轴上点对应的数是,点对应的数是,,垂足为,且,以为圆心,长为半径画弧,交数轴于点,则点表示的数为
A. B. C. D.
9.如图,以数轴的单位长线段为边做一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点,则点表示的数是
A.1 B.1.4 C. D.
10.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点表示的数是,,若以点为圆心、的长为半径画弧,与数轴交于点(点位于点右侧),则点表示的数为 .
11.《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”
译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?丈尺).
答:折断处离地面的高度为
A.3尺 B.尺 C.4尺 D.4.55尺
12.在以下列长度为边长的4个正方形铁片中,若要剪出一个直角边长分别为和的直角三角形铁片,则符合要求的正方形铁片边长的最小值为
A. B. C. D.
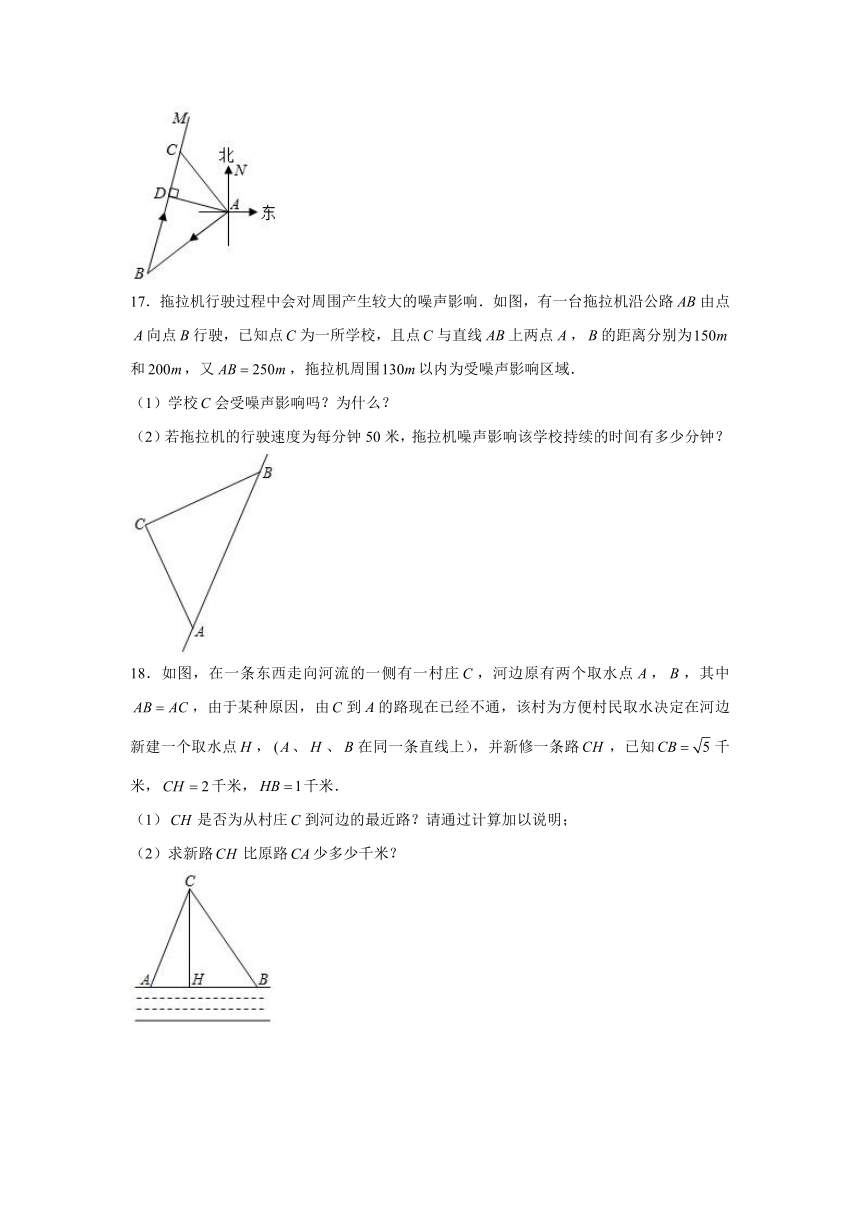
13.某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆数是 (参考数据:,,
A.1 B.2 C.3 D.4
14.某会展中心在会展期间准备将高、长、宽的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要 元.
15.如图,在数轴上,点、表示的数分别为0、2,于点,且,连接,在上截取,以为圆心,的长为半径画弧,交线段于点,则点表示的实数是 .
16.一艘轮船从港向南偏西方向航行到达岛,再从岛沿方向航行到达岛,港到航线的最短距离是.
(1)若轮船速度为小时,求轮船从岛沿返回港所需的时间.
(2)岛在港的什么方向?
17.拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路由点向点行驶,已知点为一所学校,且点与直线上两点,的距离分别为和,又,拖拉机周围以内为受噪声影响区域.
(1)学校会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
18.如图,在一条东西走向河流的一侧有一村庄,河边原有两个取水点,,其中,由于某种原因,由到的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点,、、在同一条直线上),并新修一条路,已知千米,千米,千米.
(1)是否为从村庄到河边的最近路?请通过计算加以说明;
(2)求新路比原路少多少千米?
参考答案
1.解:在中,,,.
,
;
在中,,,
.
故选:.
2.解:如图,由题意,,米,米,旗杆折断之前的高度高度就是.
在中,,米,米,
(米,
旗杆折断之前的高度高度(米,
故选:.
3.解:.,
,
.
,
.
故梯足将滑动的距离是.
故选:.
4.解:如图,过点作于点,
米,米,米,
(米.
在中,由勾股定理得到:(米
故选:.
5.解:取的中点,过作于,如图2所示:
由题意得:,
设寸,
则(寸,寸,寸,
寸,
在中,
,即,
解得:,
(寸,
寸,
故答案为:101.
6.解:在中,,
,
,
点在轴负半轴,
点表示的数为.
故选:.
7.解:点,对应的实数分别为1,3,
,
,
,
,
则,
点对应的实数为,
故选:.
8.解:,
,
,
以为圆心,为半径画弧,交数轴于点,
,
点表示的数是:,
故选:.
9.解:由勾股定理得,,
则,
点表示的数是,
故选:.
10.解:由勾股定理得,,,
设点表示的数为,则,
,
故答案为:.
11.解:设竹子折断处离地面尺,则斜边为尺,
根据勾股定理得:,
解得:,
答:折断处离地面的高度为4.55尺;
故选:.
12.解:如图所示:
是直角三角形,,,,
,
四边形是正方形,
,,
,
,
,
,
设,则,
,
在中,由勾股定理得:,
解得:,
.
故选:.
13.解:车宽2米,
卡车能否通过,只要比较距厂门中线1米处的高度与车高.
在中,由勾股定理可得:
(米,
,
两辆卡车都能通过此门,
故选:.
14.解:由勾股定理得,
则地毯总长为,
则地毯的总面积为(平方米),
所以铺完这个楼道至少需要(元.
故答案为:680.
15.解:,
,
,,
,
,
,
,
,
点表示的实数是.
故答案为:.
16.解:(1)由题意,
中,,得.
.
.
.
(小时).
答:从岛返回港所需的时间为3小时.
(2),,
.
.
.
岛在港的北偏西.
17.解:(1)学校会受噪声影响.
理由:如图,过点作于,
,,,
.
是直角三角形.
,
,
,
拖拉机周围以内为受噪声影响区域域,
学校会受噪声影响.
(2)当,时,正好影响学校,
,
,
拖拉机的行驶速度为每分钟50米,
(分钟),
即拖拉机噪声影响该学校持续的时间有2分钟.
18.解:(1)是从村庄到河边的最近路.
理由如下:
,,,
,
为直角三角形,,
,
为点到的最短路线;
(2)设,则,,
在中,,解得,
即,
,
答:新路比原路少0.5千米.
第2课时 勾股定理的应用
1.如图所示是某房屋顶框架的示意图,其中,,,,则的长度为
A. B. C. D.
2.一根旗杆在离地面3米处断裂,旗杆顶部落在离旗杆底部4米处,旗杆折断之前的高度是
A.5米 B.7米 C.8米 D.9米
3.如图,一架长的梯子靠在一竖直的墙上,这时梯子的底端到墙根的距离为,如果梯子的顶端下滑至,那么梯子底端将滑动
A. B. C. D.
4.如图,某自动感应门的正上方处装着一个感应器,离地米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生正对门,缓慢走到离门1.2米的地方时米),感应门自动打开,则人头顶离感应器的距离等于
A.1.2米 B.1.5米 C.2.0米 D.2.5米
5.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙的距离为2寸,点和点距离门槛都为1尺尺寸),则的长是 寸.
6.如图数轴上的点表示的数是0,点表示的数是2,,垂足为,且,以为圆心,长为半径画弧,交数轴于点,则点表示的数为
A. B. C. D.
7.如图,在数轴上,点,对应的实数分别为1,3,,,以点为圆心,为半径画弧交数轴正半轴于点,则点对应的实数为
A. B. C. D.
8.如图,数轴上点对应的数是,点对应的数是,,垂足为,且,以为圆心,长为半径画弧,交数轴于点,则点表示的数为
A. B. C. D.
9.如图,以数轴的单位长线段为边做一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点,则点表示的数是
A.1 B.1.4 C. D.
10.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点表示的数是,,若以点为圆心、的长为半径画弧,与数轴交于点(点位于点右侧),则点表示的数为 .
11.《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”
译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:折断处离地面有多高?丈尺).
答:折断处离地面的高度为
A.3尺 B.尺 C.4尺 D.4.55尺
12.在以下列长度为边长的4个正方形铁片中,若要剪出一个直角边长分别为和的直角三角形铁片,则符合要求的正方形铁片边长的最小值为
A. B. C. D.
13.某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆数是 (参考数据:,,
A.1 B.2 C.3 D.4
14.某会展中心在会展期间准备将高、长、宽的楼道铺上地毯,已知地毯每平方米20元,请你帮助计算一下,铺完这个楼道至少需要 元.
15.如图,在数轴上,点、表示的数分别为0、2,于点,且,连接,在上截取,以为圆心,的长为半径画弧,交线段于点,则点表示的实数是 .
16.一艘轮船从港向南偏西方向航行到达岛,再从岛沿方向航行到达岛,港到航线的最短距离是.
(1)若轮船速度为小时,求轮船从岛沿返回港所需的时间.
(2)岛在港的什么方向?
17.拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路由点向点行驶,已知点为一所学校,且点与直线上两点,的距离分别为和,又,拖拉机周围以内为受噪声影响区域.
(1)学校会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?
18.如图,在一条东西走向河流的一侧有一村庄,河边原有两个取水点,,其中,由于某种原因,由到的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点,、、在同一条直线上),并新修一条路,已知千米,千米,千米.
(1)是否为从村庄到河边的最近路?请通过计算加以说明;
(2)求新路比原路少多少千米?
参考答案
1.解:在中,,,.
,
;
在中,,,
.
故选:.
2.解:如图,由题意,,米,米,旗杆折断之前的高度高度就是.
在中,,米,米,
(米,
旗杆折断之前的高度高度(米,
故选:.
3.解:.,
,
.
,
.
故梯足将滑动的距离是.
故选:.
4.解:如图,过点作于点,
米,米,米,
(米.
在中,由勾股定理得到:(米
故选:.
5.解:取的中点,过作于,如图2所示:
由题意得:,
设寸,
则(寸,寸,寸,
寸,
在中,
,即,
解得:,
(寸,
寸,
故答案为:101.
6.解:在中,,
,
,
点在轴负半轴,
点表示的数为.
故选:.
7.解:点,对应的实数分别为1,3,
,
,
,
,
则,
点对应的实数为,
故选:.
8.解:,
,
,
以为圆心,为半径画弧,交数轴于点,
,
点表示的数是:,
故选:.
9.解:由勾股定理得,,
则,
点表示的数是,
故选:.
10.解:由勾股定理得,,,
设点表示的数为,则,
,
故答案为:.
11.解:设竹子折断处离地面尺,则斜边为尺,
根据勾股定理得:,
解得:,
答:折断处离地面的高度为4.55尺;
故选:.
12.解:如图所示:
是直角三角形,,,,
,
四边形是正方形,
,,
,
,
,
,
设,则,
,
在中,由勾股定理得:,
解得:,
.
故选:.
13.解:车宽2米,
卡车能否通过,只要比较距厂门中线1米处的高度与车高.
在中,由勾股定理可得:
(米,
,
两辆卡车都能通过此门,
故选:.
14.解:由勾股定理得,
则地毯总长为,
则地毯的总面积为(平方米),
所以铺完这个楼道至少需要(元.
故答案为:680.
15.解:,
,
,,
,
,
,
,
,
点表示的实数是.
故答案为:.
16.解:(1)由题意,
中,,得.
.
.
.
(小时).
答:从岛返回港所需的时间为3小时.
(2),,
.
.
.
岛在港的北偏西.
17.解:(1)学校会受噪声影响.
理由:如图,过点作于,
,,,
.
是直角三角形.
,
,
,
拖拉机周围以内为受噪声影响区域域,
学校会受噪声影响.
(2)当,时,正好影响学校,
,
,
拖拉机的行驶速度为每分钟50米,
(分钟),
即拖拉机噪声影响该学校持续的时间有2分钟.
18.解:(1)是从村庄到河边的最近路.
理由如下:
,,,
,
为直角三角形,,
,
为点到的最短路线;
(2)设,则,,
在中,,解得,
即,
,
答:新路比原路少0.5千米.
