2021-2022学年人教版八年级数学下册 17.1 第1课时 勾股定理的认识 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 17.1 第1课时 勾股定理的认识 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 632.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 17:21:23 | ||
图片预览



文档简介
17.1 勾股定理
第1课时 勾股定理的认识
1.在中,两条直角边的长分别为5和12,则斜边的长为
A.6 B.7 C.10 D.13
2.直角三角形的两条边长为5和12,它的斜边长为
A.13 B. C.13或 D.13或12
3.若直角三角形的三边长分别为3,5,,则的可能值有
A.1个 B.2个 C.3个 D.4个
4.直角三角形的两直角边分别为,,斜边为,则下列关于,,三边的关系式不正确的是
A. B. C. D.
5.已知中,,,,.
(1)若,.求;
(2)若,.求.
6.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边,在一条直线上,证明中用到的面积相等关系是
A.
B.
C.
D.
7.如图,“赵爽弦图”由4个全等的直角三角形所围成,在中,,,,若图中大正方形的面积为48,小正方形的面积为6,则的值为
A.60 B.79 C.84 D.90
8.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明,请将下面说理过程补充完整:
证明:连接,过点作边上的高,交的延长线与点,
则四边形为长方形,所以 .(用含字母的代数式表示)
因为 ;
;
所以 ;
所以 .
9.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为,较小的直角边长都为,斜边长都为,大正方形的面积可以表示为,也可以表示为,所以,即.由此推导出重要的勾股定理:如果直角三角形两条直角边长为,,斜边长为,则.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形的两直角边长为3和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释,画在上面的网格中,并标出字母,所表示的线段.
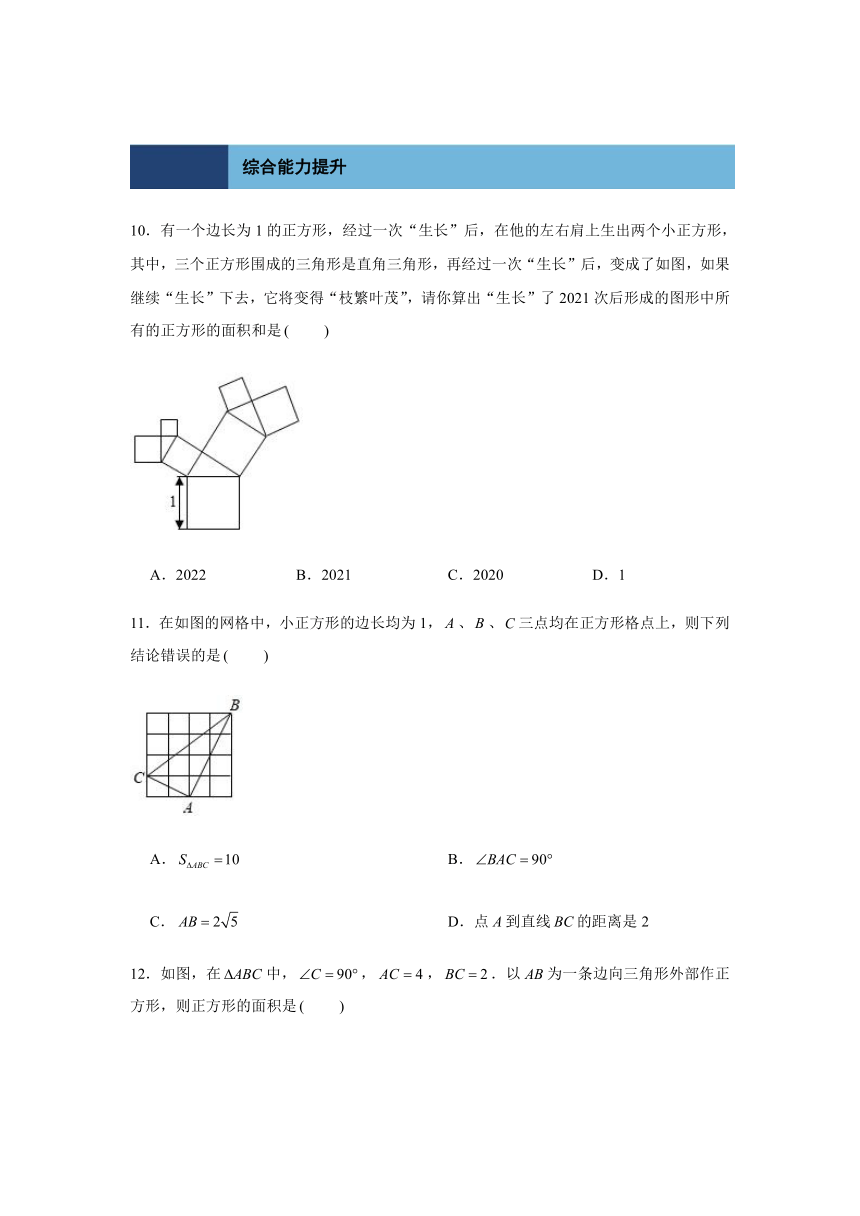
10.有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是
A.2022 B.2021 C.2020 D.1
11.在如图的网格中,小正方形的边长均为1,、、三点均在正方形格点上,则下列结论错误的是
A. B.
C. D.点到直线的距离是2
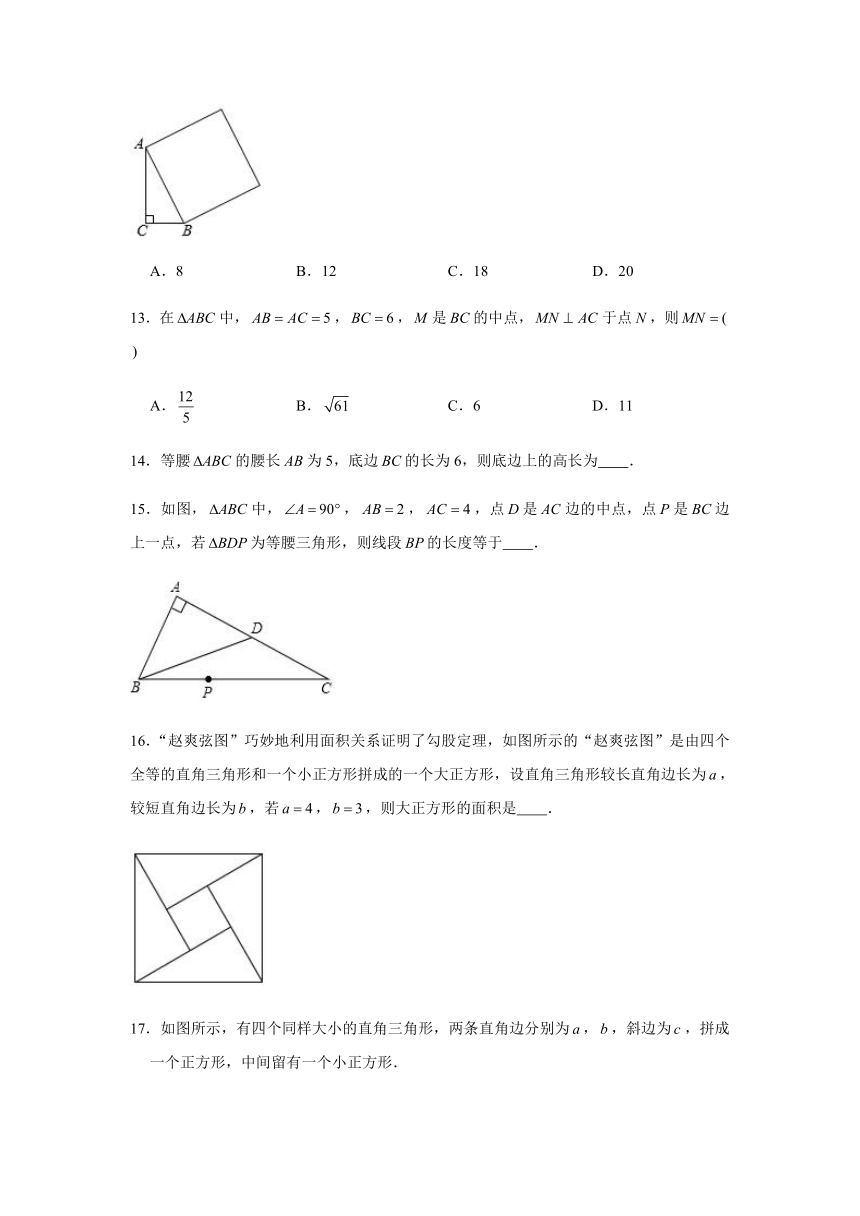
12.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是
A.8 B.12 C.18 D.20
13.在中,,,是的中点,于点,则
A. B. C.6 D.11
14.等腰的腰长为5,底边的长为6,则底边上的高长为 .
15.如图,中,,,,点是边的中点,点是边上一点,若为等腰三角形,则线段的长度等于 .
16.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,,则大正方形的面积是 .
17.如图所示,有四个同样大小的直角三角形,两条直角边分别为,,斜边为,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于,,的等式;
(2)利用(1)中发现的直角三角形中两直角边,和斜边之间的关系,完成问题:如图,在直角中,,且,,则的面积为 ;
(3)如图③,大正方形的边长为,小正方形的边长为,若用、表示四个矩形的两边长,观察图案,指出以下关系式:
(1) (2) (3)(4) 其中正确的有 (填序号)
参考答案
.2..3..4..
5.解:(1),,,,,,
,
即的值是;
(2),,,,,,
,
即的值是8.
6..
7..
8.证明:连接,过点作边上的高,交的延长线与点,
则四边形为长方形,所以.(用含字母的代数式表示)
因为;
;
所以;
所以.
故答案为:;;;;;;;.
9.解:(1)梯形的面积为,
也利用表示为,
,
即;
(2)直角三角形的两直角边分别为3,4,
斜边为5,
设斜边上的高为,直角三角形的面积为,
,
故答案为;
(3)图形面积为:,
边长为,
由此可画出的图形为:
10..11..12..13..14.4.
15.解:如图,当时,
连接交于点,过作于,于.
点是边的中点,,
,
,
,
,
垂直平分线段,
,
,
,
,
在中,,
,
垂直平分,
,,
,
,,
在中,;
当时,,
综上所述,线段的长度为或,
故答案为:或.
16.25.
17.解:(1)大正方形的面积,
大正方形的面积,
,
,
即
(2),
,即,
又,
,即,
的面积为
故答案为:7;
(3)矩形的边长分别为,,
矩形的面积;
大正方形的边长为,
;
小正方形的边长为,
,
;
,,
;
故其中正确的有(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
第1课时 勾股定理的认识
1.在中,两条直角边的长分别为5和12,则斜边的长为
A.6 B.7 C.10 D.13
2.直角三角形的两条边长为5和12,它的斜边长为
A.13 B. C.13或 D.13或12
3.若直角三角形的三边长分别为3,5,,则的可能值有
A.1个 B.2个 C.3个 D.4个
4.直角三角形的两直角边分别为,,斜边为,则下列关于,,三边的关系式不正确的是
A. B. C. D.
5.已知中,,,,.
(1)若,.求;
(2)若,.求.
6.1876年,美国总统伽菲尔德利用如图所示的方法验证了勾股定理,其中两个全等的直角三角形的边,在一条直线上,证明中用到的面积相等关系是
A.
B.
C.
D.
7.如图,“赵爽弦图”由4个全等的直角三角形所围成,在中,,,,若图中大正方形的面积为48,小正方形的面积为6,则的值为
A.60 B.79 C.84 D.90
8.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明,请将下面说理过程补充完整:
证明:连接,过点作边上的高,交的延长线与点,
则四边形为长方形,所以 .(用含字母的代数式表示)
因为 ;
;
所以 ;
所以 .
9.(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为,较小的直角边长都为,斜边长都为,大正方形的面积可以表示为,也可以表示为,所以,即.由此推导出重要的勾股定理:如果直角三角形两条直角边长为,,斜边长为,则.图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形的两直角边长为3和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释,画在上面的网格中,并标出字母,所表示的线段.
10.有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是
A.2022 B.2021 C.2020 D.1
11.在如图的网格中,小正方形的边长均为1,、、三点均在正方形格点上,则下列结论错误的是
A. B.
C. D.点到直线的距离是2
12.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是
A.8 B.12 C.18 D.20
13.在中,,,是的中点,于点,则
A. B. C.6 D.11
14.等腰的腰长为5,底边的长为6,则底边上的高长为 .
15.如图,中,,,,点是边的中点,点是边上一点,若为等腰三角形,则线段的长度等于 .
16.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,,则大正方形的面积是 .
17.如图所示,有四个同样大小的直角三角形,两条直角边分别为,,斜边为,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于,,的等式;
(2)利用(1)中发现的直角三角形中两直角边,和斜边之间的关系,完成问题:如图,在直角中,,且,,则的面积为 ;
(3)如图③,大正方形的边长为,小正方形的边长为,若用、表示四个矩形的两边长,观察图案,指出以下关系式:
(1) (2) (3)(4) 其中正确的有 (填序号)
参考答案
.2..3..4..
5.解:(1),,,,,,
,
即的值是;
(2),,,,,,
,
即的值是8.
6..
7..
8.证明:连接,过点作边上的高,交的延长线与点,
则四边形为长方形,所以.(用含字母的代数式表示)
因为;
;
所以;
所以.
故答案为:;;;;;;;.
9.解:(1)梯形的面积为,
也利用表示为,
,
即;
(2)直角三角形的两直角边分别为3,4,
斜边为5,
设斜边上的高为,直角三角形的面积为,
,
故答案为;
(3)图形面积为:,
边长为,
由此可画出的图形为:
10..11..12..13..14.4.
15.解:如图,当时,
连接交于点,过作于,于.
点是边的中点,,
,
,
,
,
垂直平分线段,
,
,
,
,
在中,,
,
垂直平分,
,,
,
,,
在中,;
当时,,
综上所述,线段的长度为或,
故答案为:或.
16.25.
17.解:(1)大正方形的面积,
大正方形的面积,
,
,
即
(2),
,即,
又,
,即,
的面积为
故答案为:7;
(3)矩形的边长分别为,,
矩形的面积;
大正方形的边长为,
;
小正方形的边长为,
,
;
,,
;
故其中正确的有(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
