2021-2022学年京改版八年级下册数学第14章一次函数 单元测试(word解析版)
文档属性
| 名称 | 2021-2022学年京改版八年级下册数学第14章一次函数 单元测试(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 111.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 17:34:24 | ||
图片预览




文档简介
2021-2022学年北京课改新版八年级下册数学《第14章 一次函数》单元测试卷
一.选择题
1.在平面直角坐标系中,点M(﹣3,6)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在如图所示的直角坐标系中,M,N的坐标分别为( )
A.M(2,﹣1),N(2,1) B.M(﹣1,2),N(2,1)
C.M(﹣1,2),N(1,2) D.M(2,﹣1),N(1,2)
3.在平面直角坐标系中,点P(5,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知点P(﹣3,﹣3),Q(﹣3,4),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
5.点A(﹣1,3)和点B(﹣1,﹣1),则A,B相距( )
A.4个单位长度 B.12个单位长度
C.10个单位长度 D.8个单位长度
6.某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量 B.数100和η都是常量
C.η和t是变量 D.数100和t都是常量
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
8.在平面直角坐标系中,点M(﹣1,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.在平面直角坐标系中,对于坐标P(3,4),下列说法错误的是( )
A.P(3,4)表示这个点在平面内的位置
B.点P的纵坐标是:4
C.点P到x轴的距离是4
D.它与点(4,3)表示同一个坐标
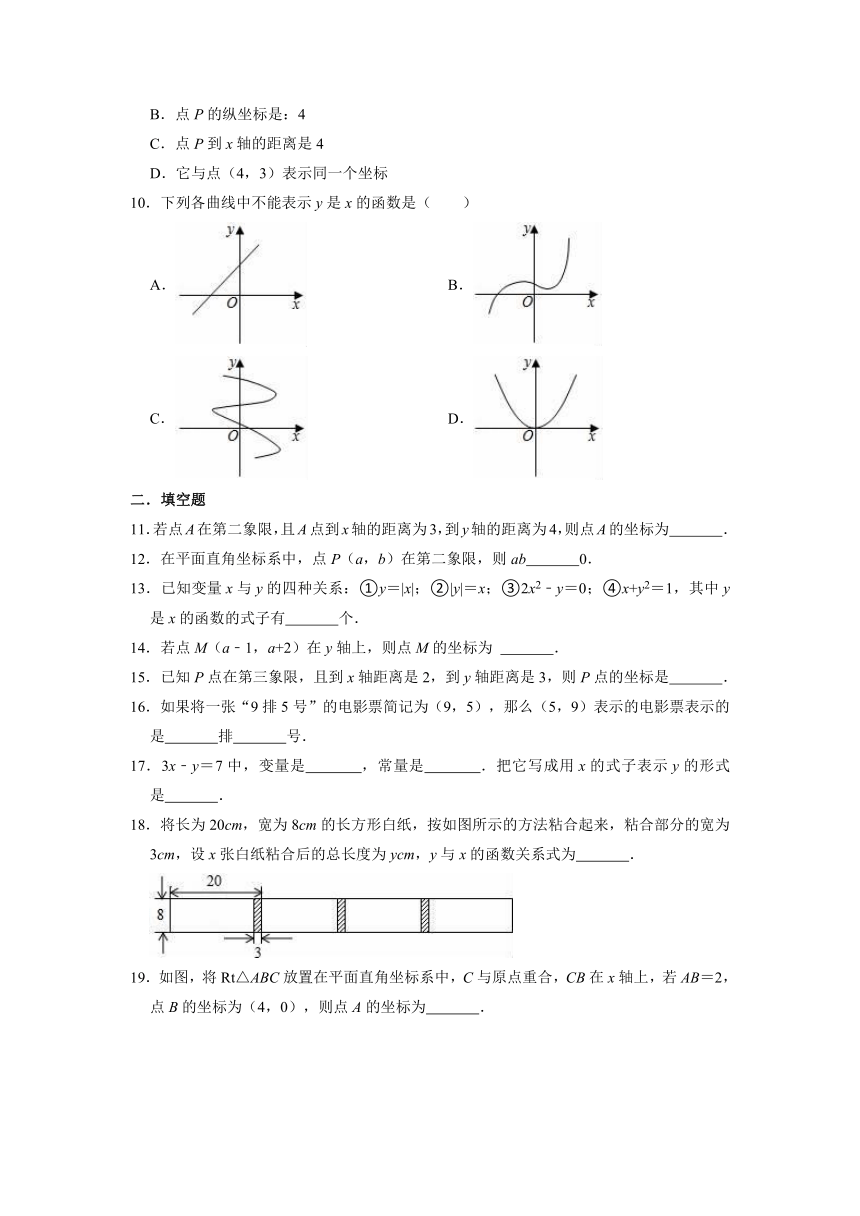
10.下列各曲线中不能表示y是x的函数是( )
A. B.
C. D.
二.填空题
11.若点A在第二象限,且A点到x轴的距离为3,到y轴的距离为4,则点A的坐标为 .
12.在平面直角坐标系中,点P(a,b)在第二象限,则ab 0.
13.已知变量x与y的四种关系:①y=|x|;②|y|=x;③2x2﹣y=0;④x+y2=1,其中y是x的函数的式子有 个.
14.若点M(a﹣1,a+2)在y轴上,则点M的坐标为 .
15.已知P点在第三象限,且到x轴距离是2,到y轴距离是3,则P点的坐标是 .
16.如果将一张“9排5号”的电影票简记为(9,5),那么(5,9)表示的电影票表示的是 排 号.
17.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
18.将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
19.如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为 .
20.点P(﹣2,﹣3)和点Q(3,﹣3)的距离为 .
三.解答题
21.已知:如图,写出坐标平面内各点的坐标.
A( , );B( , );
C( , );D( , );
E( , );F( , ).
22.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)当点M到x轴的距离为1时,求点M的坐标;
(2)当点M到y轴的距离为2时,求点M的坐标.
23.李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
24.在边长1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点)
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
25.根据要求解答下列问题:
设M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意实数,且b<0时,点M位于何处?
26.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
27.阅读下列一段文字,然后回答下列问题:
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.
例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.
特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.
(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
参考答案与试题解析
一.选择题
1.解:点M(﹣3,6)在第二象限,
故选:B.
2.解:点M在第二象限,那么横坐标小于0,是﹣1,纵坐标大于0,是2,即M点的坐标为(﹣1,2);
又因为点N在第一象限,那么它的横,纵坐标都大于0,即N的坐标为(2,1).
故选:B.
3.解:点P(5,﹣3)在第四象限.
故选:D.
4.解:∵P(﹣3,﹣3),Q(﹣3,4),
∴P、Q横坐标相等,
∴由坐标特征知直线PQ平行于y轴,
故选:B.
5.解:∵点A(﹣1,3)和点B(﹣1,﹣1)的横坐标都是﹣1,
∴A,B相距|﹣1﹣3|=4个单位长度.
故选:A.
6.解:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中:η和t是变量,零件的个数100是常量.
故选:C.
7.解:①x是自变量,y是因变量;正确;
②x的数值可以任意选择;正确;
③y是变量,它的值与x无关;而y随x的变化而变化;错误;
④用关系式表示的不能用图象表示;错误;
⑤y与x的关系还可以用列表法和图象法表示,正确;
故选:A.
8.解:点M(﹣1,1)在第二象限.
故选:B.
9.解:A、P(3,4)表示这个点在平面内的位置,正确,不合题意;
B、点P的纵坐标是:4,正确,不合题意;
C、点P到x轴的距离是4,正确,不合题意;
D、它与点(4,3)不是同一个坐标,故此选项错误,符合题意.
故选:D.
10.解:A、B、D选项中,对于一定范围内自变量x的任何值,y都有唯一的值与之相对应,所以y是x的函数;
C选项中,对于一定范围内x取值时,y可能有2个值与之相对应,所以y不是x的函数;
故选:C.
二.填空题
11.解:∵点A在第二象限,且A点到x轴的距离为3,
∴点A的纵坐标为3,
∵点A到y轴的距离为4,
∴点A的横坐标是﹣4,
∴点A的坐标为(﹣4,3).
故答案为:(﹣4,3).
12.解:∵点P(a,b)在第二象限,
∴a<0,b>0,
∴ab<0,
故答案为:<.
13.y是x的函数的式子有:①y=|x|;③2x2﹣y=0,共2个,
故答案为:2.
14.解:∵点M(a﹣1,a+2)在y轴上,
∴a﹣1=0,
解得:a=1,
则a+2=3,
则点M的坐标为:(0,3).
故答案为:(0,3).
15.解:∵第三象限内的点横坐标<0,纵坐标<0,
点P到x轴的距离是2,到y轴的距离为3,
∴点P的纵坐标为﹣2,横坐标为﹣3,
因而点P的坐标是(﹣3,﹣2),
故答案为:(﹣3,﹣2).
16.解:∵“9排5号”的电影票简记为(9,5),
∴(5,9)的电影票表示为5排9号.
故答案为5,9.
17.解:3x﹣y=7中,变量是x和y,常量是3和﹣7.把它写成用x的式子表示y的形式是y=3x﹣7.
故答案是:x和y;3和﹣7;y=3x﹣7.
18.解:由题意得:y=20x﹣(x﹣1)×3=17x+3,
故答案为:y=17x+3.
19.解:作AD⊥OB于D,如图所示
∵点B的坐标为(4,0),
∴OB=4,
∵∠OAB=90°,AB=2,
∴OA==2,
∵△OAB的面积=OB AD=OA AB,
∴AD===,
∴OD==3,
∴A(3,);
故答案为:(3,).
20.解:点P和点Q的间的距离==5.
故答案为5.
三.解答题
21.解:坐标平面内各点的坐标A(﹣5,0),B(0,﹣3),C(5,﹣2),D(3,2),E(0,2),F(﹣3,4),
故答案为:﹣5,0;0,﹣3;5,﹣2;3,2;0,2;﹣3,4.
22.解:(1)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M的坐标是(﹣2,1)或(﹣3,﹣1);
(2)∵|m﹣1|=2,
∴m﹣1=2或m﹣1=﹣2,
解得:m=3或m=﹣1,
∴点M的坐标是:(2,9)或(﹣2,1).
23.解:(1)如图,
坐标原点在F点,
(2)A(0,4)、B(﹣3,2)、C(﹣2,﹣1)、E(3,3);
(3)AF=400米.
24.解:(1)由图可知点A(4,1)、B(0,0)、C(﹣2,3)、D(2,4);
(2)四边形ABCD的面积=4×6﹣×2×3﹣×1×4﹣×2×3﹣×1×4=14.
25.解:∵M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第四象限;
(2)当ab>0时,即a,b同号,故点M位于第一、三象限;
(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.
26.解:(1)∵点A在y轴上,
∴3a﹣5=0,
解得:a=,
a+1=,
点A的坐标为:(0,);
(2)∵点A到x轴的距离与到y轴的距离相等,
∴|3a﹣5|=|a+1|,
①3a﹣5=a+1,解得:a=3,则点A(4,4);
②3a﹣5+(a+1)=0,解得:a=1,则点A(﹣2,2);
所以a=3,则点A(4,4)或a=1,则点A(﹣2,2).
27.解:(1)AB==;
(2)AB=5﹣(﹣1)=6;
(3)△ABC为直角三角形.理由如下:
∵AB==,AC==2,BC==5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形.
一.选择题
1.在平面直角坐标系中,点M(﹣3,6)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在如图所示的直角坐标系中,M,N的坐标分别为( )
A.M(2,﹣1),N(2,1) B.M(﹣1,2),N(2,1)
C.M(﹣1,2),N(1,2) D.M(2,﹣1),N(1,2)
3.在平面直角坐标系中,点P(5,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.已知点P(﹣3,﹣3),Q(﹣3,4),则直线PQ( )
A.平行于x轴 B.平行于y轴
C.垂直于y轴 D.以上都不正确
5.点A(﹣1,3)和点B(﹣1,﹣1),则A,B相距( )
A.4个单位长度 B.12个单位长度
C.10个单位长度 D.8个单位长度
6.某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中,下列说法正确的是( )
A.数100和η,t都是变量 B.数100和η都是常量
C.η和t是变量 D.数100和t都是常量
7.在关系式y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④用关系式表示的不能用图象表示;⑤y与x的关系还可以用列表法和图象法表示,其中说法正确的是( )
A.①②⑤ B.①②④ C.①③⑤ D.①④⑤
8.在平面直角坐标系中,点M(﹣1,1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.在平面直角坐标系中,对于坐标P(3,4),下列说法错误的是( )
A.P(3,4)表示这个点在平面内的位置
B.点P的纵坐标是:4
C.点P到x轴的距离是4
D.它与点(4,3)表示同一个坐标
10.下列各曲线中不能表示y是x的函数是( )
A. B.
C. D.
二.填空题
11.若点A在第二象限,且A点到x轴的距离为3,到y轴的距离为4,则点A的坐标为 .
12.在平面直角坐标系中,点P(a,b)在第二象限,则ab 0.
13.已知变量x与y的四种关系:①y=|x|;②|y|=x;③2x2﹣y=0;④x+y2=1,其中y是x的函数的式子有 个.
14.若点M(a﹣1,a+2)在y轴上,则点M的坐标为 .
15.已知P点在第三象限,且到x轴距离是2,到y轴距离是3,则P点的坐标是 .
16.如果将一张“9排5号”的电影票简记为(9,5),那么(5,9)表示的电影票表示的是 排 号.
17.3x﹣y=7中,变量是 ,常量是 .把它写成用x的式子表示y的形式是 .
18.将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
19.如图,将Rt△ABC放置在平面直角坐标系中,C与原点重合,CB在x轴上,若AB=2,点B的坐标为(4,0),则点A的坐标为 .
20.点P(﹣2,﹣3)和点Q(3,﹣3)的距离为 .
三.解答题
21.已知:如图,写出坐标平面内各点的坐标.
A( , );B( , );
C( , );D( , );
E( , );F( , ).
22.已知平面直角坐标系中有一点M(m﹣1,2m+3).
(1)当点M到x轴的距离为1时,求点M的坐标;
(2)当点M到y轴的距离为2时,求点M的坐标.
23.李老师到人民公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点和x轴、y轴.只知道游乐园D的坐标为(2,﹣2).
(1)帮李老师在图中建立平面直角坐标系;
(2)求出其他各景点的坐标.
(3)若图中一个单位长度代表实际距离100米,请你求出其中某两点(已用字母标记)间的实际距离.
24.在边长1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点)
(1)写出点A,B,C,D的坐标;
(2)求四边形ABCD的面积.
25.根据要求解答下列问题:
设M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意实数,且b<0时,点M位于何处?
26.在平面直角坐标系中,点A的坐标是(3a﹣5,a+1)
(1)若点A在y轴上,求a的值及点A的坐标.
(2)若点A到x轴的距离与到y轴的距离相等;求a的值及点A的坐标.
27.阅读下列一段文字,然后回答下列问题:
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:MN=.
例如:已知P(3,1)、Q(1,﹣2),则这两点的距离PQ==.
特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1﹣x2|或|y1﹣y2|.
(1)已知A(1,2)、B(﹣2,﹣3),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
参考答案与试题解析
一.选择题
1.解:点M(﹣3,6)在第二象限,
故选:B.
2.解:点M在第二象限,那么横坐标小于0,是﹣1,纵坐标大于0,是2,即M点的坐标为(﹣1,2);
又因为点N在第一象限,那么它的横,纵坐标都大于0,即N的坐标为(2,1).
故选:B.
3.解:点P(5,﹣3)在第四象限.
故选:D.
4.解:∵P(﹣3,﹣3),Q(﹣3,4),
∴P、Q横坐标相等,
∴由坐标特征知直线PQ平行于y轴,
故选:B.
5.解:∵点A(﹣1,3)和点B(﹣1,﹣1)的横坐标都是﹣1,
∴A,B相距|﹣1﹣3|=4个单位长度.
故选:A.
6.解:某人要在规定的时间内加工100个零件,则工作效率η与时间t之间的关系中:η和t是变量,零件的个数100是常量.
故选:C.
7.解:①x是自变量,y是因变量;正确;
②x的数值可以任意选择;正确;
③y是变量,它的值与x无关;而y随x的变化而变化;错误;
④用关系式表示的不能用图象表示;错误;
⑤y与x的关系还可以用列表法和图象法表示,正确;
故选:A.
8.解:点M(﹣1,1)在第二象限.
故选:B.
9.解:A、P(3,4)表示这个点在平面内的位置,正确,不合题意;
B、点P的纵坐标是:4,正确,不合题意;
C、点P到x轴的距离是4,正确,不合题意;
D、它与点(4,3)不是同一个坐标,故此选项错误,符合题意.
故选:D.
10.解:A、B、D选项中,对于一定范围内自变量x的任何值,y都有唯一的值与之相对应,所以y是x的函数;
C选项中,对于一定范围内x取值时,y可能有2个值与之相对应,所以y不是x的函数;
故选:C.
二.填空题
11.解:∵点A在第二象限,且A点到x轴的距离为3,
∴点A的纵坐标为3,
∵点A到y轴的距离为4,
∴点A的横坐标是﹣4,
∴点A的坐标为(﹣4,3).
故答案为:(﹣4,3).
12.解:∵点P(a,b)在第二象限,
∴a<0,b>0,
∴ab<0,
故答案为:<.
13.y是x的函数的式子有:①y=|x|;③2x2﹣y=0,共2个,
故答案为:2.
14.解:∵点M(a﹣1,a+2)在y轴上,
∴a﹣1=0,
解得:a=1,
则a+2=3,
则点M的坐标为:(0,3).
故答案为:(0,3).
15.解:∵第三象限内的点横坐标<0,纵坐标<0,
点P到x轴的距离是2,到y轴的距离为3,
∴点P的纵坐标为﹣2,横坐标为﹣3,
因而点P的坐标是(﹣3,﹣2),
故答案为:(﹣3,﹣2).
16.解:∵“9排5号”的电影票简记为(9,5),
∴(5,9)的电影票表示为5排9号.
故答案为5,9.
17.解:3x﹣y=7中,变量是x和y,常量是3和﹣7.把它写成用x的式子表示y的形式是y=3x﹣7.
故答案是:x和y;3和﹣7;y=3x﹣7.
18.解:由题意得:y=20x﹣(x﹣1)×3=17x+3,
故答案为:y=17x+3.
19.解:作AD⊥OB于D,如图所示
∵点B的坐标为(4,0),
∴OB=4,
∵∠OAB=90°,AB=2,
∴OA==2,
∵△OAB的面积=OB AD=OA AB,
∴AD===,
∴OD==3,
∴A(3,);
故答案为:(3,).
20.解:点P和点Q的间的距离==5.
故答案为5.
三.解答题
21.解:坐标平面内各点的坐标A(﹣5,0),B(0,﹣3),C(5,﹣2),D(3,2),E(0,2),F(﹣3,4),
故答案为:﹣5,0;0,﹣3;5,﹣2;3,2;0,2;﹣3,4.
22.解:(1)∵|2m+3|=1,
∴2m+3=1或2m+3=﹣1,
解得:m=﹣1或m=﹣2,
∴点M的坐标是(﹣2,1)或(﹣3,﹣1);
(2)∵|m﹣1|=2,
∴m﹣1=2或m﹣1=﹣2,
解得:m=3或m=﹣1,
∴点M的坐标是:(2,9)或(﹣2,1).
23.解:(1)如图,
坐标原点在F点,
(2)A(0,4)、B(﹣3,2)、C(﹣2,﹣1)、E(3,3);
(3)AF=400米.
24.解:(1)由图可知点A(4,1)、B(0,0)、C(﹣2,3)、D(2,4);
(2)四边形ABCD的面积=4×6﹣×2×3﹣×1×4﹣×2×3﹣×1×4=14.
25.解:∵M(a,b)为平面直角坐标系中的点.
(1)当a>0,b<0时,点M位于第四象限;
(2)当ab>0时,即a,b同号,故点M位于第一、三象限;
(3)当a为任意实数,且b<0时,点M位于第三、四象限和纵轴的负半轴.
26.解:(1)∵点A在y轴上,
∴3a﹣5=0,
解得:a=,
a+1=,
点A的坐标为:(0,);
(2)∵点A到x轴的距离与到y轴的距离相等,
∴|3a﹣5|=|a+1|,
①3a﹣5=a+1,解得:a=3,则点A(4,4);
②3a﹣5+(a+1)=0,解得:a=1,则点A(﹣2,2);
所以a=3,则点A(4,4)或a=1,则点A(﹣2,2).
27.解:(1)AB==;
(2)AB=5﹣(﹣1)=6;
(3)△ABC为直角三角形.理由如下:
∵AB==,AC==2,BC==5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形.
同课章节目录
