17.1勾股定理 基础训练-2021-2022学年人教版八年级数学下册(word版含答案)
文档属性
| 名称 | 17.1勾股定理 基础训练-2021-2022学年人教版八年级数学下册(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 00:00:00 | ||
图片预览



文档简介
勾股定理
《勾股定理》同步基础训练
选择。
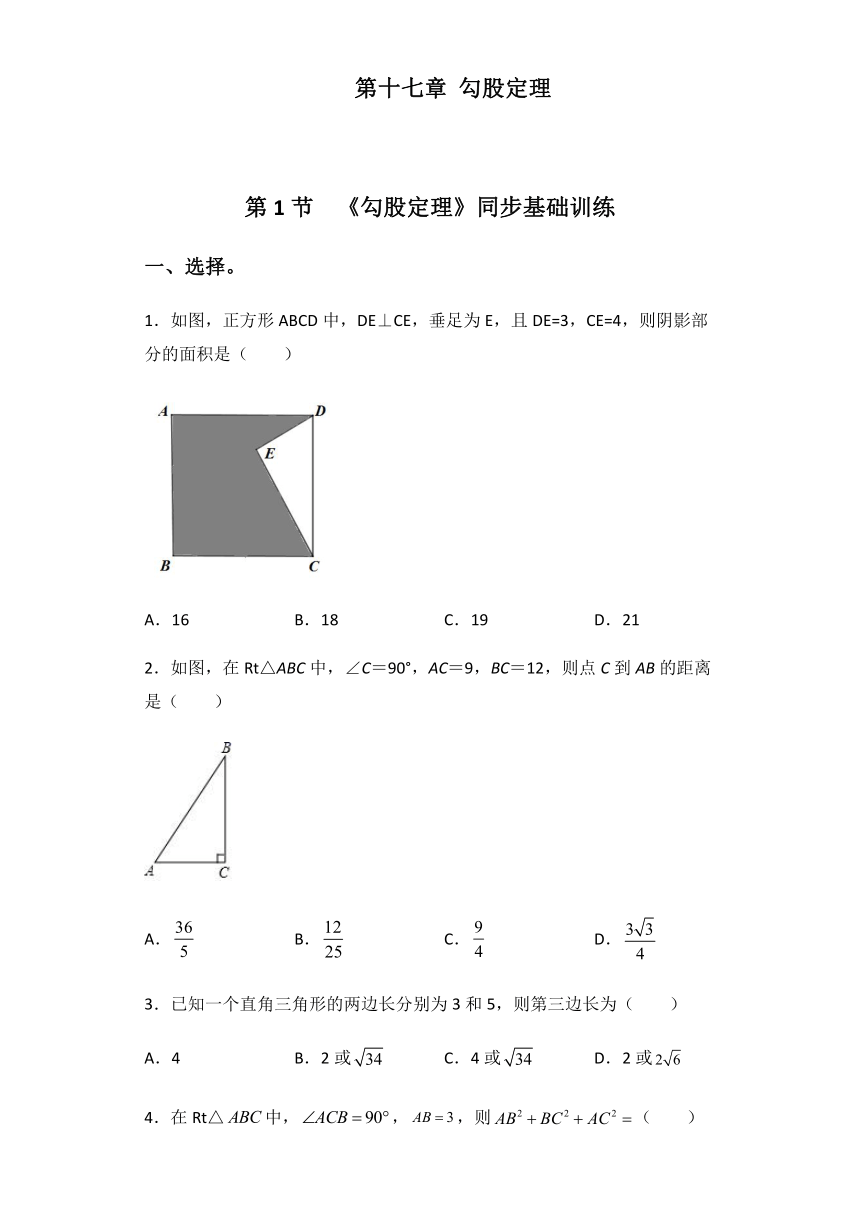
1.如图,正方形ABCD中,DE⊥CE,垂足为E,且DE=3,CE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
2.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
3.已知一个直角三角形的两边长分别为3和5,则第三边长为( )
A.4 B.2或 C.4或 D.2或
4.在Rt△中,,,则( )
A.9 B.18 C.20 D.24
5.在Rt△ABC中,∠C=90°,若AC=5,BC=12,则AB的长为( )
A.5 B.12 C.13 D.15
6.小明想知道学校旗杆的高度,她发现旗杆上的绳子刚好垂到地面,当她把绳子的下端拉开5米后,发现绳子下端距离地面1米,则旗杆的高是( )
A.8米 B.10米 C.12米 D.13米
7.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.4 D.13或5
8.如图,△ABC中,AD⊥BC于D,AB=5,BD=4,DC=2,则AC等于( )
A.13 B. C. D.5
9.如图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为( )
A.16π B.12π C.10π D.8π
10.如果Rt△的两直角边长分别为n2-1,2n(n >1),那么它的斜边长是( )
A.2n B.n+1 C.n2-1 D.n2+1
填空。
11.一个直角三角形三边长是三个连续整数,则它的周长为_______,面积为______.
12.在中,,,,______.
13.如图,长方体中,,,,一只蚂蚁从点A出发,以秒的速度沿长方体表面爬行到点,至少需要______ 分钟.
14.观察下列式子:
当时,,,,3,4,5是一组勾股数;
当时,,,,6,8,10是一组勾股数;
当时,,,,8,15,17是一组勾股数……
根据以上规律,用含(的整数)的代数式表示具备上述特点的勾股数 _______, _______,_______.
15.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行_____米.
解答。
16.如图,要为一段高,长的楼梯铺上红地毯.问:红地毯至少需要多少米?
17.如图,在Rt△ABC中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=______,BD=_____.
18.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
19.规范表达(严格按格式):如图,已知∠A=90°,AC=5,AB=12,BE=3.求长方形的面积.
20.(古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
答案
1-5:CACBC
6-10:DDBDD
11.12 6
12.12
13.
14.; ; .
15.10米
需要爬行的最短路径是17cm.
【详解】
根据勾股定理,楼梯水平长度为(米),则红地毯至少要12+5=17米长,故答案为:17m.
17.8, 6.4
【详解】
∵∠ADC=∠ACB=90°,∠CAD=∠BAC,
∴△ACD~△ABC,
∴,
∴AC2=AB AD,
∵AC=6,AD=3.6,
∴36=3.6AB,AB=10,
在直角三角形ABC中,BC2=AB2﹣AC2=100﹣36=64,
∴BC=8.
BD=AB-AD=10-3.6=6.4
18.7
【解析】
∵AD⊥AC,AC=20,AD=15,
∴CD==25,
∴BD=BC﹣CD=32﹣25=7.
19.39
【解析】
在RtΔABC中,∠A=90°,AB=12,AC=5,
∴BC=
∴长方形BCDE的面积=13×3=39.
20.水深3.75尺.
【详解】
解:设水深x尺,则荷花茎的长度为x+0.5,
根据勾股定理得:(x+0.5)2=x2+4
解得:x=3.75.
答:湖水深3.75尺.
试卷第1页,总3页
《勾股定理》同步基础训练
选择。
1.如图,正方形ABCD中,DE⊥CE,垂足为E,且DE=3,CE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
2.如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
A. B. C. D.
3.已知一个直角三角形的两边长分别为3和5,则第三边长为( )
A.4 B.2或 C.4或 D.2或
4.在Rt△中,,,则( )
A.9 B.18 C.20 D.24
5.在Rt△ABC中,∠C=90°,若AC=5,BC=12,则AB的长为( )
A.5 B.12 C.13 D.15
6.小明想知道学校旗杆的高度,她发现旗杆上的绳子刚好垂到地面,当她把绳子的下端拉开5米后,发现绳子下端距离地面1米,则旗杆的高是( )
A.8米 B.10米 C.12米 D.13米
7.一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5 C.4 D.13或5
8.如图,△ABC中,AD⊥BC于D,AB=5,BD=4,DC=2,则AC等于( )
A.13 B. C. D.5
9.如图,在Rt△ABC中,∠B=90°,BC=15,AC=17,以AB为直径作半圆,则此半圆的面积为( )
A.16π B.12π C.10π D.8π
10.如果Rt△的两直角边长分别为n2-1,2n(n >1),那么它的斜边长是( )
A.2n B.n+1 C.n2-1 D.n2+1
填空。
11.一个直角三角形三边长是三个连续整数,则它的周长为_______,面积为______.
12.在中,,,,______.
13.如图,长方体中,,,,一只蚂蚁从点A出发,以秒的速度沿长方体表面爬行到点,至少需要______ 分钟.
14.观察下列式子:
当时,,,,3,4,5是一组勾股数;
当时,,,,6,8,10是一组勾股数;
当时,,,,8,15,17是一组勾股数……
根据以上规律,用含(的整数)的代数式表示具备上述特点的勾股数 _______, _______,_______.
15.如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行_____米.
解答。
16.如图,要为一段高,长的楼梯铺上红地毯.问:红地毯至少需要多少米?
17.如图,在Rt△ABC中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=______,BD=_____.
18.如图,△ABC中,AB=AC=20,BC=32,D是BC上一点,AD=15,且AD⊥AC,求BD长.
19.规范表达(严格按格式):如图,已知∠A=90°,AC=5,AB=12,BE=3.求长方形的面积.
20.(古代数学问题)印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”,该问题是:“平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;“渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.
答案
1-5:CACBC
6-10:DDBDD
11.12 6
12.12
13.
14.; ; .
15.10米
需要爬行的最短路径是17cm.
【详解】
根据勾股定理,楼梯水平长度为(米),则红地毯至少要12+5=17米长,故答案为:17m.
17.8, 6.4
【详解】
∵∠ADC=∠ACB=90°,∠CAD=∠BAC,
∴△ACD~△ABC,
∴,
∴AC2=AB AD,
∵AC=6,AD=3.6,
∴36=3.6AB,AB=10,
在直角三角形ABC中,BC2=AB2﹣AC2=100﹣36=64,
∴BC=8.
BD=AB-AD=10-3.6=6.4
18.7
【解析】
∵AD⊥AC,AC=20,AD=15,
∴CD==25,
∴BD=BC﹣CD=32﹣25=7.
19.39
【解析】
在RtΔABC中,∠A=90°,AB=12,AC=5,
∴BC=
∴长方形BCDE的面积=13×3=39.
20.水深3.75尺.
【详解】
解:设水深x尺,则荷花茎的长度为x+0.5,
根据勾股定理得:(x+0.5)2=x2+4
解得:x=3.75.
答:湖水深3.75尺.
试卷第1页,总3页
