17.1勾股定理 训练-2020-2021学年人教版八年级数学下册(word版含答案)
文档属性
| 名称 | 17.1勾股定理 训练-2020-2021学年人教版八年级数学下册(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 20:02:32 | ||
图片预览



文档简介
第17章 勾股定理
第1节 《勾股定理》同步训练
1、选择。
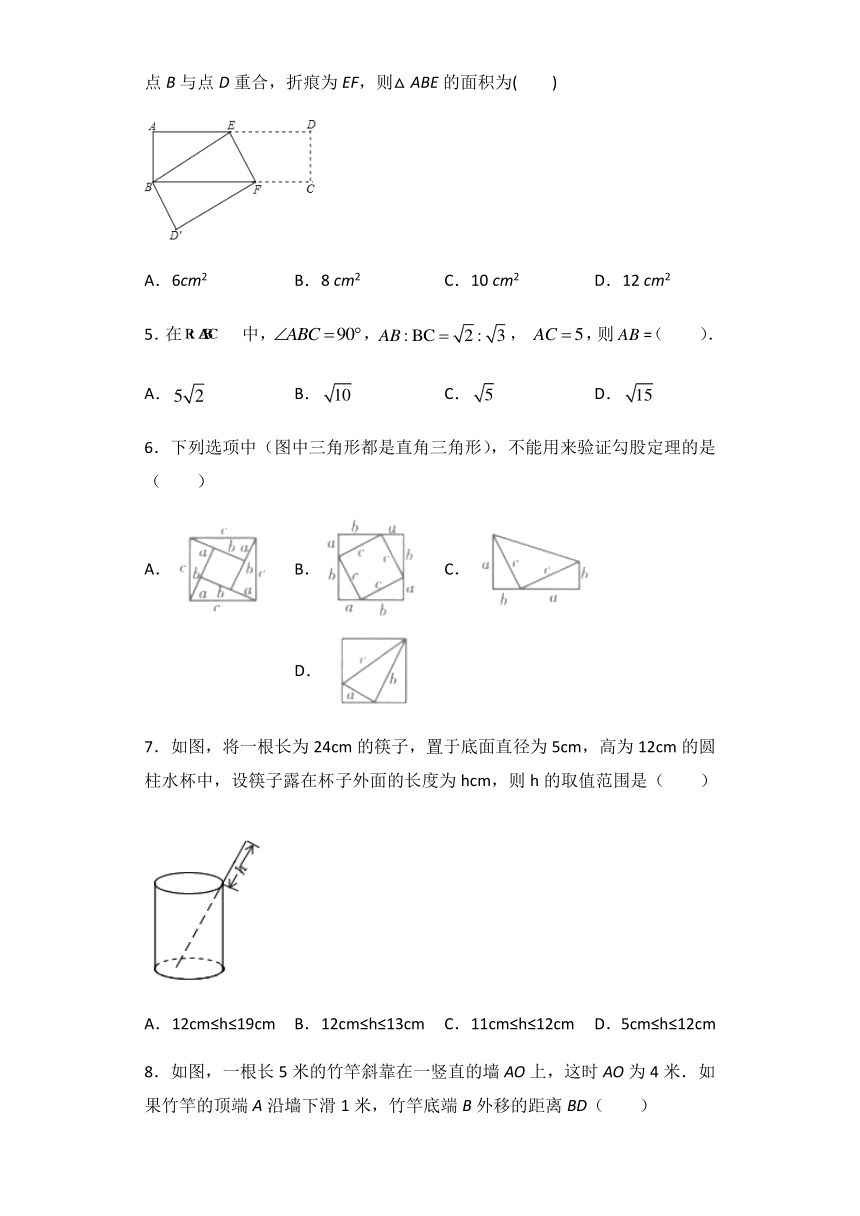
1.如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC,垂足为E,若DE=1,CD,则BE=( )
A. B.2 C. D.
2.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则BC的长是( )
A. B.2 C. D.
3.如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
A.16 B.8 C.4 D.2
4.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8 cm2 C.10 cm2 D.12 cm2
5.在中,,, ,则=( ).
A. B. C. D.
6.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是( )
A. B. C. D.
7.如图,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.12cm≤h≤19cm B.12cm≤h≤13cm C.11cm≤h≤12cm D.5cm≤h≤12cm
8.如图,一根长5米的竹竿斜靠在一竖直的墙AO上,这时AO为4米.如果竹竿的顶端A沿墙下滑1米,竹竿底端B外移的距离BD( )
A.等于1米 B.大于1米 C.小于1米 D.以上都不对
9.直角三角形一直角边长为12,另两条边长均为自然数,则其周长为().
A.30 B.28 C.56 D.不能确定
10.如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
2、填空。
11.如图,矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足是E,那么BE=________,CE=________.
12.如图所示,在一个高为6米,长为10米,宽为2.5米的楼梯表面铺地毯.若每平方米地毯50元铺满整个楼梯至少需_________元.
13.在直角三角形中,,,,分别为,,的对边,若,,则________.
14.如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用_____秒钟.
15.在△ABC中,AB=15,AC=13,高AD=12,则的周长为_______________.
三、解答。
16.如图,四边形ABCD中,∠ADC=90°,AD=4cm,CD=3cm,AB=13cm,BC=12cm,求这个四边形的面积?
17.在一棵树的10米高处有两只猴子,其中一只猴子爬下树走到离树20米的池塘,另一只猴子爬到树顶后直接跃向池塘的处,如果两只猴子所经过距离相等,试问这棵树有多高.
18.在中,,,,求斜边上的高.
19.如图所示,水池中离岸边点1.5米的处直立着一根芦苇,露出水面部分的长是0.5米,把芦苇拉到岸边,它的顶端恰好落在点,求水池中水的深度.
20.如图,在中,,,,.
求的周长;
判断是否是直角三角形,并说明理由.
答案
1-5:BDBAB
6-10:DCADB
11.
12.1750
13.48
14.2.5秒.
15.32或42
16.24cm2
【详解】
解:连接AC,
∵AD=4cm,CD=3cm,∠ADC=90°,
∴AC==5(cm)
∴S△ACD=CD AD=6(cm2).
在△ABC中,∵52+122=132,即AC2+BC2=AB2,
∴△ABC为直角三角形,即∠ACB=90°,
∴S△ABC=AC BC=30(cm2).
∴S四边形ABCD=S△ABC﹣S△ACD
=30﹣6=24(cm2).
答:四边形ABCD的面积为24cm2.
17.树高为15m.
【详解】
解:设树高BC为xm,则CD=x-10,
则题意可知BD+AB=10+20=30,
∴AC=30-CD=30-(x-10)=40-x,
∵△ABC为直角三角形,
∴AC2=AB2+BC2,即(40-x)2=202+x2,
解得x=15,即树高为15m,
18.2
【详解】
∵BC:AC=1:2,
∴设BC=k,AC=2k,
由勾股定理得,BC2+AC2=AB2,
即k2+(2k)2=52,
解得k=,
所以,BC=,AC=2,
设AB边长的高为h,
则S△ABC=×5h=××2,
解得h=2,
即斜边AB上的高为2.
19.2米.
【解析】
设水池中水的深度为米,
则米.
在中,根据勾股定理,
得,
即.
解得.
所以水池中水的深度为2米.
20.(1)54;(2)不是直角三角形,理由见解析.
【详解】
解:,
.
在和中,
根据勾股定理得,,
又,,,
,
;
不是直角三角形.理由:
,
,
不是直角三角形.
试卷第1页,总3页
第1节 《勾股定理》同步训练
1、选择。
1.如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC,垂足为E,若DE=1,CD,则BE=( )
A. B.2 C. D.
2.如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则BC的长是( )
A. B.2 C. D.
3.如图,已知阴影部分是一个正方形,AB=4,∠B=45°,此正方形的面积( )
A.16 B.8 C.4 D.2
4.已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8 cm2 C.10 cm2 D.12 cm2
5.在中,,, ,则=( ).
A. B. C. D.
6.下列选项中(图中三角形都是直角三角形),不能用来验证勾股定理的是( )
A. B. C. D.
7.如图,将一根长为24cm的筷子,置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.12cm≤h≤19cm B.12cm≤h≤13cm C.11cm≤h≤12cm D.5cm≤h≤12cm
8.如图,一根长5米的竹竿斜靠在一竖直的墙AO上,这时AO为4米.如果竹竿的顶端A沿墙下滑1米,竹竿底端B外移的距离BD( )
A.等于1米 B.大于1米 C.小于1米 D.以上都不对
9.直角三角形一直角边长为12,另两条边长均为自然数,则其周长为().
A.30 B.28 C.56 D.不能确定
10.如图,一个圆柱形油罐,油罐的底面周长12m,高5m,要从点A环绕油罐建梯子,正好到达点A的正上方的点B,则梯子最短需要( )
A.12m B.13m C.17m D.20m
2、填空。
11.如图,矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足是E,那么BE=________,CE=________.
12.如图所示,在一个高为6米,长为10米,宽为2.5米的楼梯表面铺地毯.若每平方米地毯50元铺满整个楼梯至少需_________元.
13.在直角三角形中,,,,分别为,,的对边,若,,则________.
14.如图所示一棱长为3cm的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm,假设一只蚂蚁每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用_____秒钟.
15.在△ABC中,AB=15,AC=13,高AD=12,则的周长为_______________.
三、解答。
16.如图,四边形ABCD中,∠ADC=90°,AD=4cm,CD=3cm,AB=13cm,BC=12cm,求这个四边形的面积?
17.在一棵树的10米高处有两只猴子,其中一只猴子爬下树走到离树20米的池塘,另一只猴子爬到树顶后直接跃向池塘的处,如果两只猴子所经过距离相等,试问这棵树有多高.
18.在中,,,,求斜边上的高.
19.如图所示,水池中离岸边点1.5米的处直立着一根芦苇,露出水面部分的长是0.5米,把芦苇拉到岸边,它的顶端恰好落在点,求水池中水的深度.
20.如图,在中,,,,.
求的周长;
判断是否是直角三角形,并说明理由.
答案
1-5:BDBAB
6-10:DCADB
11.
12.1750
13.48
14.2.5秒.
15.32或42
16.24cm2
【详解】
解:连接AC,
∵AD=4cm,CD=3cm,∠ADC=90°,
∴AC==5(cm)
∴S△ACD=CD AD=6(cm2).
在△ABC中,∵52+122=132,即AC2+BC2=AB2,
∴△ABC为直角三角形,即∠ACB=90°,
∴S△ABC=AC BC=30(cm2).
∴S四边形ABCD=S△ABC﹣S△ACD
=30﹣6=24(cm2).
答:四边形ABCD的面积为24cm2.
17.树高为15m.
【详解】
解:设树高BC为xm,则CD=x-10,
则题意可知BD+AB=10+20=30,
∴AC=30-CD=30-(x-10)=40-x,
∵△ABC为直角三角形,
∴AC2=AB2+BC2,即(40-x)2=202+x2,
解得x=15,即树高为15m,
18.2
【详解】
∵BC:AC=1:2,
∴设BC=k,AC=2k,
由勾股定理得,BC2+AC2=AB2,
即k2+(2k)2=52,
解得k=,
所以,BC=,AC=2,
设AB边长的高为h,
则S△ABC=×5h=××2,
解得h=2,
即斜边AB上的高为2.
19.2米.
【解析】
设水池中水的深度为米,
则米.
在中,根据勾股定理,
得,
即.
解得.
所以水池中水的深度为2米.
20.(1)54;(2)不是直角三角形,理由见解析.
【详解】
解:,
.
在和中,
根据勾股定理得,,
又,,,
,
;
不是直角三角形.理由:
,
,
不是直角三角形.
试卷第1页,总3页
