2021-2022学年人教版八年级下册数学 17.1勾股定理 同步习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学 17.1勾股定理 同步习题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 208.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 00:00:00 | ||
图片预览


文档简介
17.1勾股定理 同步习题
一.选择题
1.在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是( )
A.21 B.36 C.48 D.36或48
2.直角三角形的周长为22,斜边长为10,则其面积为( )
A.22 B.11 C.24 D.48
3.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB= B.∠BAC=90°
C.S△ABC=10 D.点A到直线BC的距离是2
4.如图,数轴上的点A表示的数是0,点B表示的数是3,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A. B.+2 C.﹣2 D.2
5.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
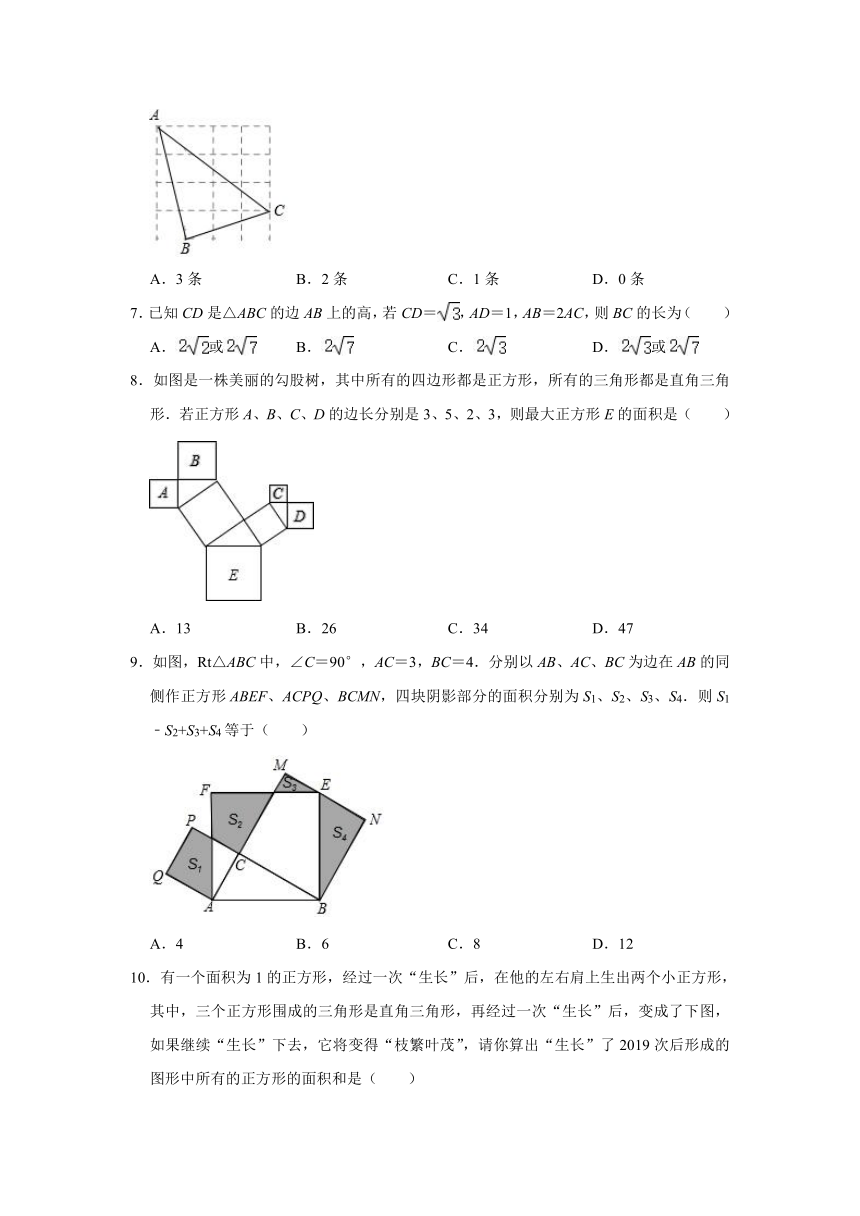
6.如图在正方形网格中,每个小正方形的边长均为1,则在△ABC中,边长为无理数的边有( )
A.3条 B.2条 C.1条 D.0条
7.已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为( )
A.或 B. C. D.或
8.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
9.如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于( )
A.4 B.6 C.8 D.12
10.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A.1 B.2018 C.2019 D.2020
二.填空题
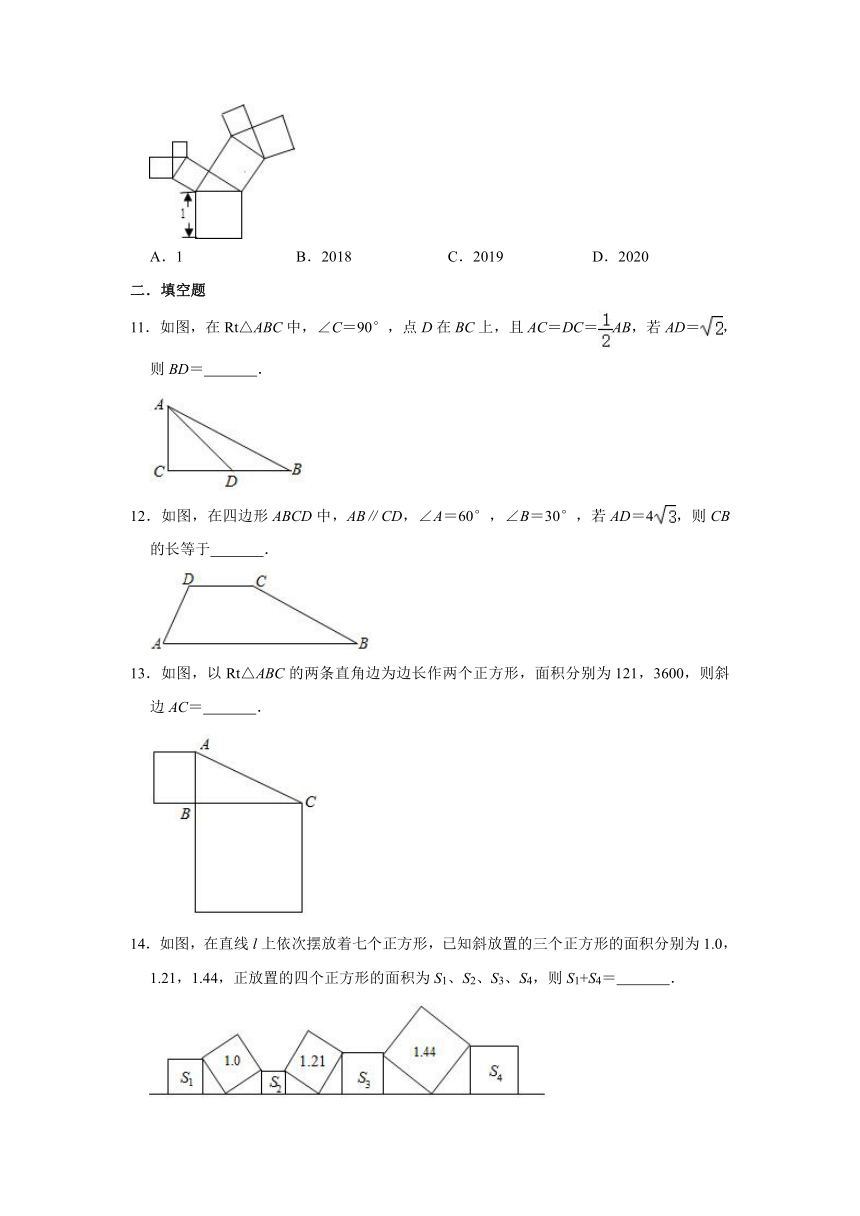
11.如图,在Rt△ABC中,∠C=90°,点D在BC上,且AC=DC=AB,若AD=,则BD= .
12.如图,在四边形ABCD中,AB∥CD,∠A=60°,∠B=30°,若AD=4,则CB的长等于 .
13.如图,以Rt△ABC的两条直角边为边长作两个正方形,面积分别为121,3600,则斜边AC= .
14.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S4= .
15.如图,四边形ABCD中,AC,BD相交于点E,∠ABC=∠DAC=90°,∠ABD=15°,AB=BC=2,则BE长为 .
三.解答题
16.在我区“五水绕城”生态环境提升项目中,有一块三角形空地将进行绿化,如图,△ABC中,AB=AC,E是AC上的一点,CE=50,BC=130,BE=120.
(1)判断△ABE的形状,并说明理由.
(2)求△ABC的周长.
17.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2﹣CD2.求证:AB=BC.
18.如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上.BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
(1)在探究长方形ACDF的面积S时,我们可以用两种不同的方法:一种是找到长和宽,然后利用长方形的面积公式,就可得到S;另一种是将长方形ACDF看成是由△ABC,△BDE,△AEF,△ABE组成的,分别求出它们的面积,再相加也可以得到S.
请根据以上材料,填空:
方法一:S= .
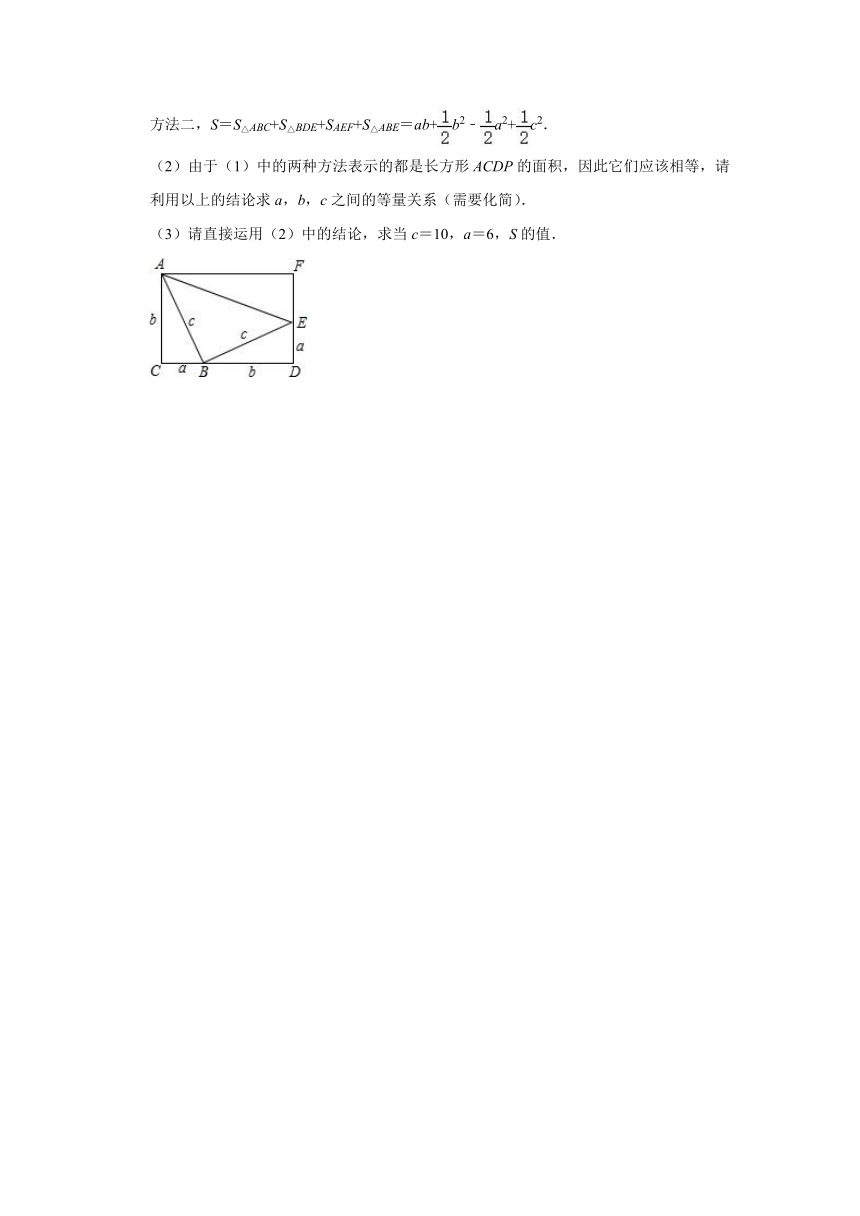
方法二,S=S△ABC+S△BDE+SAEF+S△ABE=ab+b2﹣a2+c2.
(2)由于(1)中的两种方法表示的都是长方形ACDP的面积,因此它们应该相等,请利用以上的结论求a,b,c之间的等量关系(需要化简).
(3)请直接运用(2)中的结论,求当c=10,a=6,S的值.
参考答案
一.选择题
1.解:分两种情况:
①如图1所示:
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∴BD===15,CD===6,
∴BC=BD+CD=15+6=21;
此时,△ABC的周长为:AB+BC+AC=17+10+21=48.
②如图2所示:
同①得:BD=15,CD=6,
∴BC=BD﹣CD=15﹣6=9;
此时,△ABC的周长为:AB+BC+AC=17+10+9=36.
综上所述:△ABC的周长为48或36.
故选:D.
2.解:设这个直角三角形的一条直角边为x,则另一条边为22﹣10﹣x,
由勾股定理得,x2+(12﹣x)2=102,
化简得,x(12﹣x)=22,
∴这个直角三角形的面积等于×x(12﹣x)=×22=11.
故选:B.
3.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
4.解:∵点A表示的数是0,点B表示的数是3,
∴AB=3,
又∵CB⊥AB于点B,且BC=2,
∴Rt△ABC中,AC===,
∵AC=AD,
∴AD=,
∴点D表示的数为,
故选:A.
5.解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:D.
6.解:由题意:AB==,BC==,AC==5,
则在△ABC中,边长为无理数的边有2条.
故选:B.
7.解:当△ABC是锐角三角形,如图1,
∵CD⊥AB,
∴∠CDA=90°,
由勾股定理得,AC===2,
∵AB=2AC,
∴AB=4,
∴BD=4﹣1=3,
∴BC===2,
当△ABC是钝角三角形,如图2,
同理得:AC=2,AB=4,
∴BC===2,
则BC的长为2或2,
故选:D.
8.解:由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+52=34,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=47,
故选:D.
9.解:过F作AM的垂线交AM于D,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1﹣S2+S3+S4
=(S1+S3)﹣S2+S4
=SRt△ABC﹣SRt△ABC+SRt△ABC
=6﹣6+6
=6,
故选:B.
10.解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2019次后形成的图形中所有的正方形的面积和是2020×1=2020.
故选:D.
二.填空题
11.解:∵AD=,∠C=90°,AC=DC,
∴AC=CD=1,
∵AC=DC=AB,
∴AB=2,
∴BC==,
∴BD=﹣1,
故答案为:﹣1.
12.解:过点C作CE∥AD交AB于E,
则∠CEB=∠A=60°,
∴∠ECB=180°﹣30°﹣60°=90°,
在Rt△ECB中,∠B=30°,
∴BE=2CE,
∵CE∥AD,AB∥CD,
∴四边形ADCE为平行四边形,
∴CE=AD=4,
∴BE=2CE=8,
由勾股定理得,BC===12,
故答案为:12.
13.解:∵AB2+BC2=AC2,即121+3600=112+602=612,
∴AC2=612.
∴AC=61.
故答案是:61.
14.解:由勾股定理的几何意义可知:S1+S2=1,S2+S3=1.21,S3+S4=1.44,
∴S1+S4=1.23.
故填:1.23.
15.解:∵∠ABC=90°,AB=BC=2,
∴AC===4,
过点B作BF⊥AC于F,
则BF=CF=AF=AC=2,∠FBA=45°,
∵∠ABD=15°,
∴∠FBE=30°,
∴EF=BE,
在Rt△BEF中,由勾股定理得:BE2=BF2+EF2,
即BE2=(2)2+(BE)2,
解得BE=4,BE=﹣4(舍去).
故答案为:4.
三.解答题
16.解:(1)△ABE是直角三角形,
理由:∵BC2=1302=16900,BE2=1202=14400,CE2=502=2500,
∴BE2+CE2=BC2=16900,
∴∠BEC=90°,
∴BE⊥AC,
∴△ABE是直角三角形.
(2)设AB=AC=x,则AE=x﹣50,
由(1)可知△ABE是直角三角形,
∴BE2+AE2=AB2,
∴1202+(x﹣50)2=x2,
解得x=169.
∴△ABC的周长为AB+AC+BC=169+169+130=468.
17.证明:∵在△ABC中,∠ABC=90°,
∴AB2+BC2=AC2.
∵在△ACD中,CD⊥AD,
∴AD2+CD2=AC2,
∴AB2+BC2=AD2+CD2,
又AD2=2AB2﹣CD2,
∴AB2+BC2=2AB2﹣CD2+CD2,
即AB2=BC2,
∴AB=BC.
18.解:(1)S=b(a+b)=ab+b2.
故答案为S=ab+b2;
(2)由题意得:,
∴2ab+2b2=2ab+b2﹣a2+c2,
∴a2+b2=c2;
(3)∵a2+b2=c2,且c=10,a=6,
∴62+b2=102,
∴b=8,
∴S=ab+b2=6×8+64=112.
答:S的值为112.
一.选择题
1.在△ABC中,AB=17,AC=10,高AD=8,则△ABC的周长是( )
A.21 B.36 C.48 D.36或48
2.直角三角形的周长为22,斜边长为10,则其面积为( )
A.22 B.11 C.24 D.48
3.在如图的网格中,每个小正方形的边长为1,A、B、C三点均在正方形格点上,则下列结论错误的是( )
A.AB= B.∠BAC=90°
C.S△ABC=10 D.点A到直线BC的距离是2
4.如图,数轴上的点A表示的数是0,点B表示的数是3,CB⊥AB于点B,且BC=2,以点A为圆心,AC为半径画弧交数轴于点D,则点D表示的数为( )
A. B.+2 C.﹣2 D.2
5.两个边长分别为a,b,c的直角三角形和一个两条直角边都是c的直角三角形拼成如图所示的图形,用两种不同的计算方法计算这个图形的面积,则可得等式为( )
A.(a+b)2=c2 B.(a﹣b)2=c2 C.a2﹣b2=c2 D.a2+b2=c2
6.如图在正方形网格中,每个小正方形的边长均为1,则在△ABC中,边长为无理数的边有( )
A.3条 B.2条 C.1条 D.0条
7.已知CD是△ABC的边AB上的高,若CD=,AD=1,AB=2AC,则BC的长为( )
A.或 B. C. D.或
8.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.34 D.47
9.如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1﹣S2+S3+S4等于( )
A.4 B.6 C.8 D.12
10.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A.1 B.2018 C.2019 D.2020
二.填空题
11.如图,在Rt△ABC中,∠C=90°,点D在BC上,且AC=DC=AB,若AD=,则BD= .
12.如图,在四边形ABCD中,AB∥CD,∠A=60°,∠B=30°,若AD=4,则CB的长等于 .
13.如图,以Rt△ABC的两条直角边为边长作两个正方形,面积分别为121,3600,则斜边AC= .
14.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1.0,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S4= .
15.如图,四边形ABCD中,AC,BD相交于点E,∠ABC=∠DAC=90°,∠ABD=15°,AB=BC=2,则BE长为 .
三.解答题
16.在我区“五水绕城”生态环境提升项目中,有一块三角形空地将进行绿化,如图,△ABC中,AB=AC,E是AC上的一点,CE=50,BC=130,BE=120.
(1)判断△ABE的形状,并说明理由.
(2)求△ABC的周长.
17.如图,在四边形ABFC中,∠ABC=90°,CD⊥AD,AD2=2AB2﹣CD2.求证:AB=BC.
18.如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上.BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.
(1)在探究长方形ACDF的面积S时,我们可以用两种不同的方法:一种是找到长和宽,然后利用长方形的面积公式,就可得到S;另一种是将长方形ACDF看成是由△ABC,△BDE,△AEF,△ABE组成的,分别求出它们的面积,再相加也可以得到S.
请根据以上材料,填空:
方法一:S= .
方法二,S=S△ABC+S△BDE+SAEF+S△ABE=ab+b2﹣a2+c2.
(2)由于(1)中的两种方法表示的都是长方形ACDP的面积,因此它们应该相等,请利用以上的结论求a,b,c之间的等量关系(需要化简).
(3)请直接运用(2)中的结论,求当c=10,a=6,S的值.
参考答案
一.选择题
1.解:分两种情况:
①如图1所示:
∵AD是BC边上的高,
∴∠ADB=∠ADC=90°,
∴BD===15,CD===6,
∴BC=BD+CD=15+6=21;
此时,△ABC的周长为:AB+BC+AC=17+10+21=48.
②如图2所示:
同①得:BD=15,CD=6,
∴BC=BD﹣CD=15﹣6=9;
此时,△ABC的周长为:AB+BC+AC=17+10+9=36.
综上所述:△ABC的周长为48或36.
故选:D.
2.解:设这个直角三角形的一条直角边为x,则另一条边为22﹣10﹣x,
由勾股定理得,x2+(12﹣x)2=102,
化简得,x(12﹣x)=22,
∴这个直角三角形的面积等于×x(12﹣x)=×22=11.
故选:B.
3.解:由题意可得,
AB==2,故选项A正确;
AC==,
BC==5,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,故选项B正确;
∴S△ABC==5,故选项C错误;
作AD⊥BC于点D,
则=5,
即=5,
解得,AD=2,
即点A到直线BC的距离是2,故选项D正确;
故选:C.
4.解:∵点A表示的数是0,点B表示的数是3,
∴AB=3,
又∵CB⊥AB于点B,且BC=2,
∴Rt△ABC中,AC===,
∵AC=AD,
∴AD=,
∴点D表示的数为,
故选:A.
5.解:根据题意得:S=(a+b)(a+b),S=ab+ab+c2,
(a+b)(a+b)=ab+ab+c2,即(a+b)(a+b)=ab+ab+c2,
整理得:a2+b2=c2.
故选:D.
6.解:由题意:AB==,BC==,AC==5,
则在△ABC中,边长为无理数的边有2条.
故选:B.
7.解:当△ABC是锐角三角形,如图1,
∵CD⊥AB,
∴∠CDA=90°,
由勾股定理得,AC===2,
∵AB=2AC,
∴AB=4,
∴BD=4﹣1=3,
∴BC===2,
当△ABC是钝角三角形,如图2,
同理得:AC=2,AB=4,
∴BC===2,
则BC的长为2或2,
故选:D.
8.解:由勾股定理得,正方形F的面积=正方形A的面积+正方形B的面积=32+52=34,
同理,正方形G的面积=正方形C的面积+正方形D的面积=22+32=13,
∴正方形E的面积=正方形F的面积+正方形G的面积=47,
故选:D.
9.解:过F作AM的垂线交AM于D,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1﹣S2+S3+S4
=(S1+S3)﹣S2+S4
=SRt△ABC﹣SRt△ABC+SRt△ABC
=6﹣6+6
=6,
故选:B.
10.解:设直角三角形的是三条边分别是a,b,c.
根据勾股定理,得a2+b2=c2,
即正方形A的面积+正方形B的面积=正方形C的面积=1.
推而广之,“生长”了2019次后形成的图形中所有的正方形的面积和是2020×1=2020.
故选:D.
二.填空题
11.解:∵AD=,∠C=90°,AC=DC,
∴AC=CD=1,
∵AC=DC=AB,
∴AB=2,
∴BC==,
∴BD=﹣1,
故答案为:﹣1.
12.解:过点C作CE∥AD交AB于E,
则∠CEB=∠A=60°,
∴∠ECB=180°﹣30°﹣60°=90°,
在Rt△ECB中,∠B=30°,
∴BE=2CE,
∵CE∥AD,AB∥CD,
∴四边形ADCE为平行四边形,
∴CE=AD=4,
∴BE=2CE=8,
由勾股定理得,BC===12,
故答案为:12.
13.解:∵AB2+BC2=AC2,即121+3600=112+602=612,
∴AC2=612.
∴AC=61.
故答案是:61.
14.解:由勾股定理的几何意义可知:S1+S2=1,S2+S3=1.21,S3+S4=1.44,
∴S1+S4=1.23.
故填:1.23.
15.解:∵∠ABC=90°,AB=BC=2,
∴AC===4,
过点B作BF⊥AC于F,
则BF=CF=AF=AC=2,∠FBA=45°,
∵∠ABD=15°,
∴∠FBE=30°,
∴EF=BE,
在Rt△BEF中,由勾股定理得:BE2=BF2+EF2,
即BE2=(2)2+(BE)2,
解得BE=4,BE=﹣4(舍去).
故答案为:4.
三.解答题
16.解:(1)△ABE是直角三角形,
理由:∵BC2=1302=16900,BE2=1202=14400,CE2=502=2500,
∴BE2+CE2=BC2=16900,
∴∠BEC=90°,
∴BE⊥AC,
∴△ABE是直角三角形.
(2)设AB=AC=x,则AE=x﹣50,
由(1)可知△ABE是直角三角形,
∴BE2+AE2=AB2,
∴1202+(x﹣50)2=x2,
解得x=169.
∴△ABC的周长为AB+AC+BC=169+169+130=468.
17.证明:∵在△ABC中,∠ABC=90°,
∴AB2+BC2=AC2.
∵在△ACD中,CD⊥AD,
∴AD2+CD2=AC2,
∴AB2+BC2=AD2+CD2,
又AD2=2AB2﹣CD2,
∴AB2+BC2=2AB2﹣CD2+CD2,
即AB2=BC2,
∴AB=BC.
18.解:(1)S=b(a+b)=ab+b2.
故答案为S=ab+b2;
(2)由题意得:,
∴2ab+2b2=2ab+b2﹣a2+c2,
∴a2+b2=c2;
(3)∵a2+b2=c2,且c=10,a=6,
∴62+b2=102,
∴b=8,
∴S=ab+b2=6×8+64=112.
答:S的值为112.
