2021-2022学年人教版数学八年级下册17.1-勾股定理课堂练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.1-勾股定理课堂练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 19:59:22 | ||
图片预览


文档简介
2021-2022学年人教版数学
八年级下册 17.1-勾股定理 课堂练习
选择题
在直角三角形中,若勾为3,股为4,则弦为
A. 5 B. 6 C. 7 D. 8
下列说法正确的是
A. 若a、b、c是的三边,则
B. 若a、b、c是的三边,则
C. 若a、b、c是的三边,,则
D. 若a、b、c是的三边,,则
在中,,,的对应边分别是以a,b,若,则下列等式中成立的是
A. B. C. D.
如图,等边的边长为2,则点B的坐标为
A.
B.
C.
D.
如图,字母B所代表的正方形的面积是
A.
B.
C.
D.
如图所示,在中,,,CD是AB边上的高,则线段AD的长度为
A.
B.
C.
D.
中,,,高,则BC的长为
A. 14 B. 4 C. 14或4 D. 以上都不对
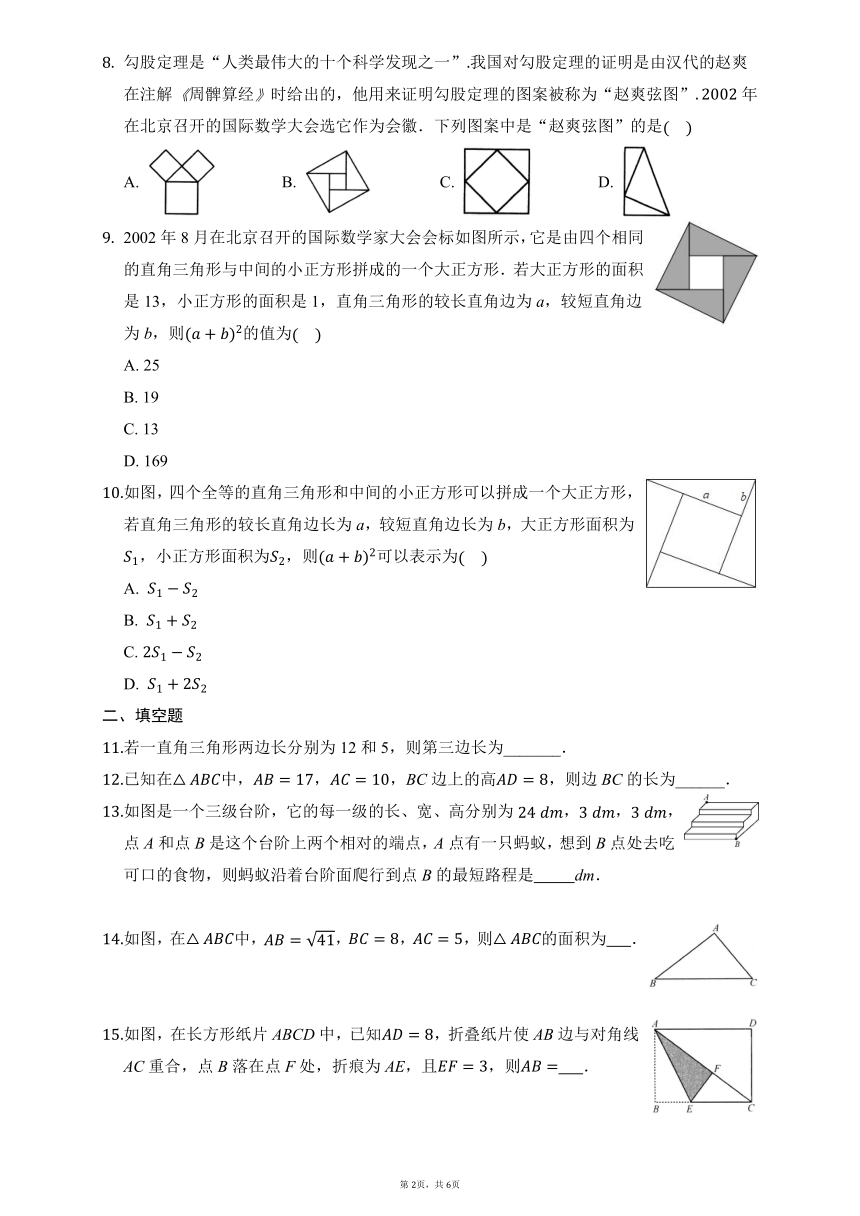
勾股定理是“人类最伟大的十个科学发现之一”我国对勾股定理的证明是由汉代的赵爽在注解周髀算经时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是
A. B. C. D.
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则的值为
A. 25
B. 19
C. 13
D. 169
如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为,小正方形面积为,则可以表示为
A.
B.
C.
D.
二、填空题
若一直角三角形两边长分别为12和5,则第三边长为_______.
已知在中,,,BC边上的高,则边BC的长为______.
如图是一个三级台阶,它的每一级的长、宽、高分别为,,,点A和点B是这个台阶上两个相对的端点,A点有一只蚂蚁,想到B点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程是 dm.
如图,在中,,,,则的面积为 .
如图,在长方形纸片ABCD中,已知,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且,则 .
三、计算题
已知直角三角形的三边长分别为a,b,c,其中两边a,b满足,求第三边长c的值.
如图,在中,,于点D,,,求BD的长.
如图所示,,,于点P,求证:。
如图,是一块等边三角形的废铁皮,利用其裁剪一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上。若所裁剪的正方形的边长为,求该等边三角形的边长。
八班小明和小亮同学学习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如下操作:
测得BD的长度为15米;注:
根据手中剩余线的长度计算出风筝线BC的长为25米;
牵线放风筝的小明身高为米.
求风筝的高度CE.
答案
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】13或
12.【答案】21或9
13.【答案】30
14.【答案】16
15.【答案】6
16.【答案】解:,
,,
,
解得,,
,b,c为直角三角形的三边长,
.
17.【答案】解:
在中,,,,
,
,
.
18.【答案】证明:是直角三角形,,
,则.
又在直角中,,
又,
,
是直角三角形,,则,
与都是直角三角形,
,
,
把代入,得
,即.
19.【答案】解:设等边三角形的边长为x,
正方形DEFG,正方形的边长为,
,
,
,
,
,
在中,
,
,
解得,或舍去,
所以该等边三角形的边长为.
20.【答案】解:风筝的高度CE为米.
第6页,共7页
第7页,共7页
八年级下册 17.1-勾股定理 课堂练习
选择题
在直角三角形中,若勾为3,股为4,则弦为
A. 5 B. 6 C. 7 D. 8
下列说法正确的是
A. 若a、b、c是的三边,则
B. 若a、b、c是的三边,则
C. 若a、b、c是的三边,,则
D. 若a、b、c是的三边,,则
在中,,,的对应边分别是以a,b,若,则下列等式中成立的是
A. B. C. D.
如图,等边的边长为2,则点B的坐标为
A.
B.
C.
D.
如图,字母B所代表的正方形的面积是
A.
B.
C.
D.
如图所示,在中,,,CD是AB边上的高,则线段AD的长度为
A.
B.
C.
D.
中,,,高,则BC的长为
A. 14 B. 4 C. 14或4 D. 以上都不对
勾股定理是“人类最伟大的十个科学发现之一”我国对勾股定理的证明是由汉代的赵爽在注解周髀算经时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是
A. B. C. D.
2002年8月在北京召开的国际数学家大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,则的值为
A. 25
B. 19
C. 13
D. 169
如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为,小正方形面积为,则可以表示为
A.
B.
C.
D.
二、填空题
若一直角三角形两边长分别为12和5,则第三边长为_______.
已知在中,,,BC边上的高,则边BC的长为______.
如图是一个三级台阶,它的每一级的长、宽、高分别为,,,点A和点B是这个台阶上两个相对的端点,A点有一只蚂蚁,想到B点处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程是 dm.
如图,在中,,,,则的面积为 .
如图,在长方形纸片ABCD中,已知,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且,则 .
三、计算题
已知直角三角形的三边长分别为a,b,c,其中两边a,b满足,求第三边长c的值.
如图,在中,,于点D,,,求BD的长.
如图所示,,,于点P,求证:。
如图,是一块等边三角形的废铁皮,利用其裁剪一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上。若所裁剪的正方形的边长为,求该等边三角形的边长。
八班小明和小亮同学学习了“勾股定理”之后,为了测得如图风筝的高度CE,他们进行了如下操作:
测得BD的长度为15米;注:
根据手中剩余线的长度计算出风筝线BC的长为25米;
牵线放风筝的小明身高为米.
求风筝的高度CE.
答案
1.【答案】A
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】A
10.【答案】C
11.【答案】13或
12.【答案】21或9
13.【答案】30
14.【答案】16
15.【答案】6
16.【答案】解:,
,,
,
解得,,
,b,c为直角三角形的三边长,
.
17.【答案】解:
在中,,,,
,
,
.
18.【答案】证明:是直角三角形,,
,则.
又在直角中,,
又,
,
是直角三角形,,则,
与都是直角三角形,
,
,
把代入,得
,即.
19.【答案】解:设等边三角形的边长为x,
正方形DEFG,正方形的边长为,
,
,
,
,
,
在中,
,
,
解得,或舍去,
所以该等边三角形的边长为.
20.【答案】解:风筝的高度CE为米.
第6页,共7页
第7页,共7页
