第五章相交线与平行线复习导学案
文档属性
| 名称 | 第五章相交线与平行线复习导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线复习导学案 序号51
备课日期:6月12日 上课日期: 主备人:阮阳
学习目标:1通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。
2、使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行的性质。
重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
难点:垂直、平行的性质和判定的综合应用。本章相交线与平行线中学习了哪些主要问题?
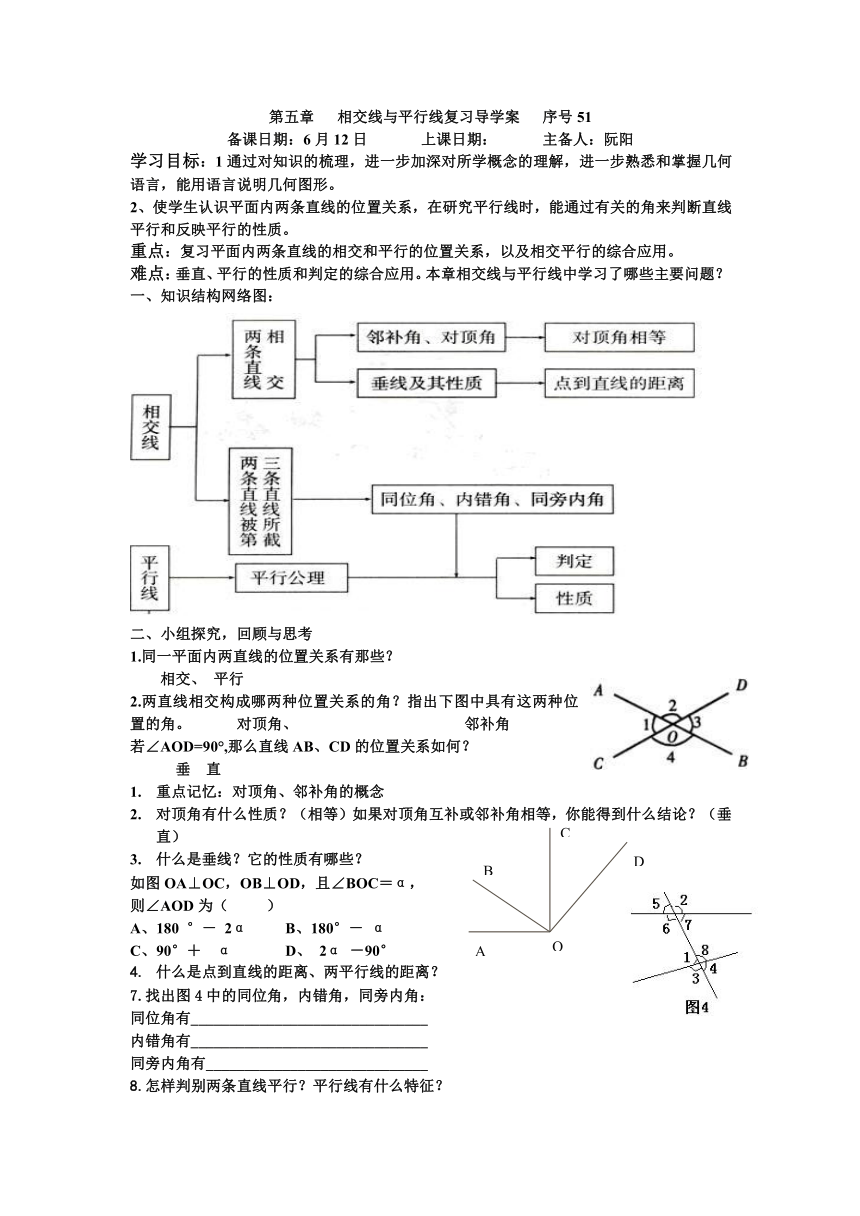
一、知识结构网络图:
二、小组探究,回顾与思考
1.同一平面内两直线的位置关系有那些?
相交、 平行
2.两直线相交构成哪两种位置关系的角?指出下图中具有这两种位置的角。 对顶角、 邻补角
若∠AOD=90°,那么直线AB、CD的位置关系如何?
垂 直
重点记忆:对顶角、邻补角的概念
对顶角有什么性质?(相等)如果对顶角互补或邻补角相等,你能得到什么结论?(垂直)
什么是垂线?它的性质有哪些?
如图OA⊥OC,OB⊥OD,且∠BOC=α,
则∠AOD为( )
A、180 °- 2α B、180°- α
C、90°+ α D、 2α -90°
什么是点到直线的距离、两平行线的距离?
7.找出图4中的同位角,内错角,同旁内角:
同位角有_______________________________
内错角有_______________________________
同旁内角有_____________________________
8.怎样判别两条直线平行?平行线有什么特征?
9.平行线的判定和性质有什么异同?
例:如图5,由∠1=∠3得___ //____( )
由∠2=∠3得___ //____( )
由∠3+∠4=180°得___ // ____( )
由∠2+∠4=180°得___ // ____( )
10.为什么研究平面内的两条直线的位置
关系总是与角联系起来?围绕这些问题
展开讨论、交流。
图5
三、课堂达标练习
1.如图1-1所示,∠AOC=360,∠DOE=900,则∠BOE=_______.
2.如图1-1中,有_________对对顶角.
3.如图1-2中,已知四条直线AB,BC,CD,DE。
问:①∠1=∠2是直线______和直线______被直线_____所截而成的____角.
②∠1=∠3是直线_____和直线_____被直线_____所截而成的____角.
③∠4=∠5是直线______和直线______被直线_____所截而成的____
角.
④∠2=∠5是直线______和直线______被直线_____所截而成的____角.
4.如图1-3:
①∵∠1=∠2,∴_____∥_____,理由是________________.
②∵AB∥DC,∴∠3=∠_______,理由是_________________.
③∵AD∥______,∴∠5=∠ADC,理由是__________________.
四、课堂反思:
第五章 相交线与平行线复习导学案 序号52
备课日期:6月12日 上课日期: 主备人:阮阳
学习目标:1通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。
2、使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行的性质。
重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
难点:垂直、平行的性质和判定的综合应用。本章相交线与平行线中学习了哪些主要问题?
基本知识点复习
1.若三条直线交于一点,则共有对顶角(平角除外)( )
A.六对 B.五对 C.四对 D.三对
2.如图1所示,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF C.∠AOF D.∠BOC和∠AOF
图1 图2 图3 图4
3. 如图2,点E在BC的延长线上,在下列四个条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
4. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
5. 如图3,AB∥CD,那么∠A,∠P,∠C的数量关系是( )
A.∠A+∠P+∠C=90° B.∠A+∠P+∠C=180°
C.∠A+∠P+∠C=360° D.∠P+∠C=∠A
6. 一个人从点A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于( ) A.75° B.105° C.45° D.135°
7.如图4所示,内错角共有( ) A.4对 B.6对 C.8对 D.10对
8.如图5所示,已知∠3=∠4,若要使∠1=∠2,则需( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.AB∥CD
9.下列说法正确的个数是( )
①同位角相等; ②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;;④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c. A.1个 B.2个 C.3个 D.4个
10. 如图6,O是正六边形ABCDEF的中心,下列图形:△OCD,△ODE,△OEF,△OAF,△OAB,其中可由△OBC平移得到的有( ) A.1个 B.2个 C.3个 D.4个
11.命题“垂直于同一直线的两直线平行”的题设是____________,结论是__________.
12.三条直线两两相交,最少有_____个交点,最多有______个交点.
13.观察图7中角的位置关系,∠1和∠2是______角,∠3和∠1是_____角,∠1和∠4是_______角,∠3和∠4是_____角,∠3和∠5是______角.
图5 图6 图7 图8
14.如图8,已知AB∥CD,∠1=70°则∠2=_______,∠3=______,∠4=______
图9 图10 图11
15.如图9所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站,做出图形,说明理由:________ _____.
16.如图10所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=______,∠AOC=_______,∠BOC=________.
17.如图11所示,四边形ABCD中,∠1=∠2,∠D=72°,则∠BCD=_______.
18. 如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是_________.
19. 已知a、b、c是同一平面内的3条直线,给出下面6个命题:a∥b, b∥c,a∥c ,a⊥b,b⊥c,a⊥c,请从中选取3个命题(其中2个作为题设,1个作为结论)尽可能多地去组成一个真命题,并说出是运用了数学中的哪个道理。举例如下:
因为a∥b, b∥c,所以a∥c(平行于同一条直线的两条直线平行)
20. 已知:如图4, AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求∠P的度数
备课日期:6月12日 上课日期: 主备人:阮阳
学习目标:1通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。
2、使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行的性质。
重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
难点:垂直、平行的性质和判定的综合应用。本章相交线与平行线中学习了哪些主要问题?
一、知识结构网络图:
二、小组探究,回顾与思考
1.同一平面内两直线的位置关系有那些?
相交、 平行
2.两直线相交构成哪两种位置关系的角?指出下图中具有这两种位置的角。 对顶角、 邻补角
若∠AOD=90°,那么直线AB、CD的位置关系如何?
垂 直
重点记忆:对顶角、邻补角的概念
对顶角有什么性质?(相等)如果对顶角互补或邻补角相等,你能得到什么结论?(垂直)
什么是垂线?它的性质有哪些?
如图OA⊥OC,OB⊥OD,且∠BOC=α,
则∠AOD为( )
A、180 °- 2α B、180°- α
C、90°+ α D、 2α -90°
什么是点到直线的距离、两平行线的距离?
7.找出图4中的同位角,内错角,同旁内角:
同位角有_______________________________
内错角有_______________________________
同旁内角有_____________________________
8.怎样判别两条直线平行?平行线有什么特征?
9.平行线的判定和性质有什么异同?
例:如图5,由∠1=∠3得___ //____( )
由∠2=∠3得___ //____( )
由∠3+∠4=180°得___ // ____( )
由∠2+∠4=180°得___ // ____( )
10.为什么研究平面内的两条直线的位置
关系总是与角联系起来?围绕这些问题
展开讨论、交流。
图5
三、课堂达标练习
1.如图1-1所示,∠AOC=360,∠DOE=900,则∠BOE=_______.
2.如图1-1中,有_________对对顶角.
3.如图1-2中,已知四条直线AB,BC,CD,DE。
问:①∠1=∠2是直线______和直线______被直线_____所截而成的____角.
②∠1=∠3是直线_____和直线_____被直线_____所截而成的____角.
③∠4=∠5是直线______和直线______被直线_____所截而成的____
角.
④∠2=∠5是直线______和直线______被直线_____所截而成的____角.
4.如图1-3:
①∵∠1=∠2,∴_____∥_____,理由是________________.
②∵AB∥DC,∴∠3=∠_______,理由是_________________.
③∵AD∥______,∴∠5=∠ADC,理由是__________________.
四、课堂反思:
第五章 相交线与平行线复习导学案 序号52
备课日期:6月12日 上课日期: 主备人:阮阳
学习目标:1通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形。
2、使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行的性质。
重点:复习平面内两条直线的相交和平行的位置关系,以及相交平行的综合应用。
难点:垂直、平行的性质和判定的综合应用。本章相交线与平行线中学习了哪些主要问题?
基本知识点复习
1.若三条直线交于一点,则共有对顶角(平角除外)( )
A.六对 B.五对 C.四对 D.三对
2.如图1所示,∠1的邻补角是( )
A.∠BOC B.∠BOE和∠AOF C.∠AOF D.∠BOC和∠AOF
图1 图2 图3 图4
3. 如图2,点E在BC的延长线上,在下列四个条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE C.∠3=∠4 D.∠D+∠DAB=180°
4. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
5. 如图3,AB∥CD,那么∠A,∠P,∠C的数量关系是( )
A.∠A+∠P+∠C=90° B.∠A+∠P+∠C=180°
C.∠A+∠P+∠C=360° D.∠P+∠C=∠A
6. 一个人从点A点出发向北偏东60°方向走到B点,再从B点出发向南偏西15°方向走到C点,那么∠ABC等于( ) A.75° B.105° C.45° D.135°
7.如图4所示,内错角共有( ) A.4对 B.6对 C.8对 D.10对
8.如图5所示,已知∠3=∠4,若要使∠1=∠2,则需( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.AB∥CD
9.下列说法正确的个数是( )
①同位角相等; ②过一点有且只有一条直线与已知直线垂直;
③过一点有且只有一条直线与已知直线平行;;④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c. A.1个 B.2个 C.3个 D.4个
10. 如图6,O是正六边形ABCDEF的中心,下列图形:△OCD,△ODE,△OEF,△OAF,△OAB,其中可由△OBC平移得到的有( ) A.1个 B.2个 C.3个 D.4个
11.命题“垂直于同一直线的两直线平行”的题设是____________,结论是__________.
12.三条直线两两相交,最少有_____个交点,最多有______个交点.
13.观察图7中角的位置关系,∠1和∠2是______角,∠3和∠1是_____角,∠1和∠4是_______角,∠3和∠4是_____角,∠3和∠5是______角.
图5 图6 图7 图8
14.如图8,已知AB∥CD,∠1=70°则∠2=_______,∠3=______,∠4=______
图9 图10 图11
15.如图9所示,在铁路旁边有一李庄,现要建一火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站,做出图形,说明理由:________ _____.
16.如图10所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=______,∠AOC=_______,∠BOC=________.
17.如图11所示,四边形ABCD中,∠1=∠2,∠D=72°,则∠BCD=_______.
18. 如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是_________.
19. 已知a、b、c是同一平面内的3条直线,给出下面6个命题:a∥b, b∥c,a∥c ,a⊥b,b⊥c,a⊥c,请从中选取3个命题(其中2个作为题设,1个作为结论)尽可能多地去组成一个真命题,并说出是运用了数学中的哪个道理。举例如下:
因为a∥b, b∥c,所以a∥c(平行于同一条直线的两条直线平行)
20. 已知:如图4, AB∥CD,直线EF分别交AB、CD于点E、F,∠BEF的平分线与∠DEF的平分线相交于点P.求∠P的度数
