2022年人教版九年级数学下册第二十七章 相似(二) 单元测试(Word版含答案)
文档属性
| 名称 | 2022年人教版九年级数学下册第二十七章 相似(二) 单元测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 557.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 18:16:25 | ||
图片预览

文档简介
初中数学九年级下册相似模拟试题(二)
一、单选题
1.如图,在平行四边形ABCD中,点E是边AD上的一点,且AE=2ED,EC交对角线BD于点F,,则( )
A.6 B.18 C.4 D.9
2.如图,在△ABC中,∠BAC=90°,AB=AC=4,点D是边BC上一动点(不与B,C重合),∠ADE=45°,DE交AC于点E,下列结论:①△ADE与△ACD一定相似;②△ABD与△DCE一定相似;③当AD=3时,;④0<CE≤2.其中正确的结论有几个?( )
A.4个 B.3个 C.2个 D.1个
3.如图,△ADC中,AD=AC,延长CD至B,使BD=CD,ED⊥BC交AB于E,EC交AD于F,下列四个结论:①EB=EC;②△BDE∽△BAC;③△ABC∽△FCD;④若AC=6,则DF=3,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
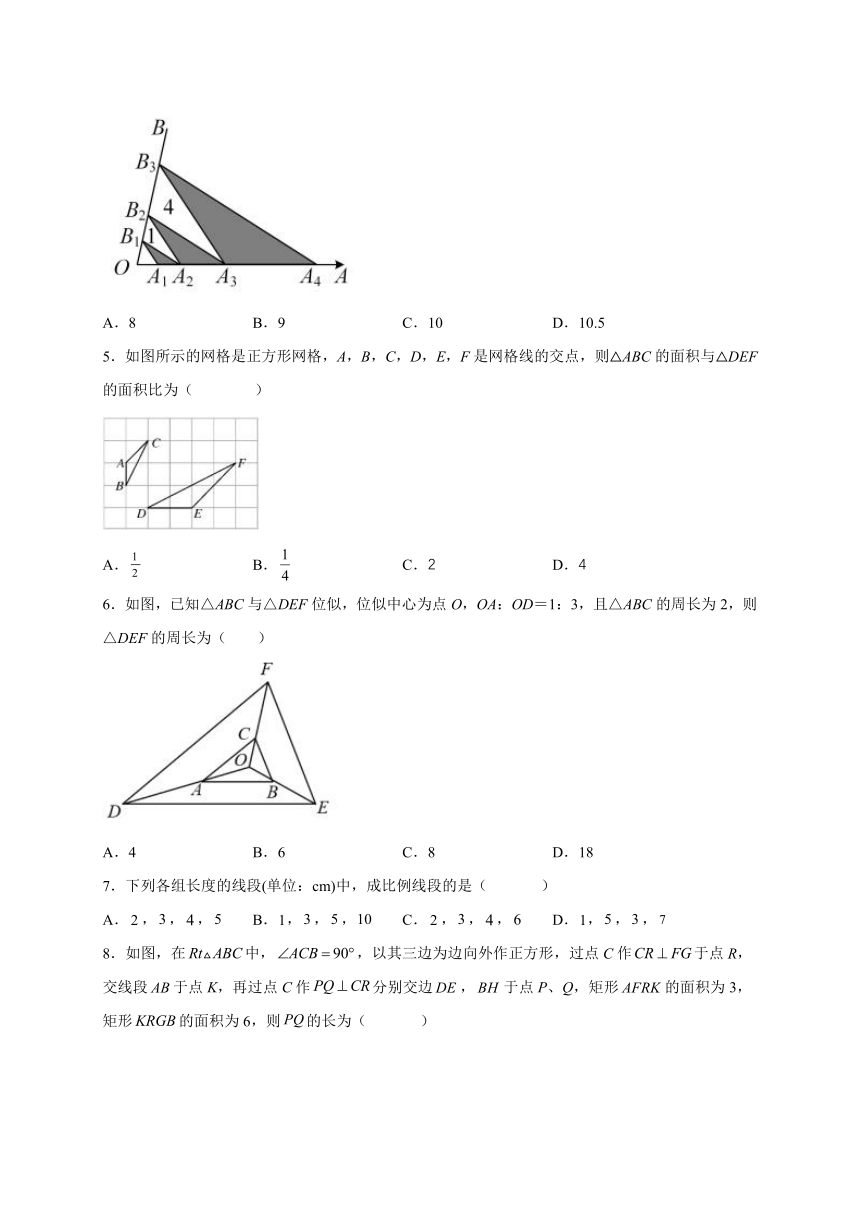
4.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
5.如图所示的网格是正方形网格,A,B,C,D,E,F是网格线的交点,则△ABC的面积与△DEF的面积比为( )
A. B. C.2 D.4
6.如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
7.下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
8.如图,在中,,以其三边为边向外作正方形,过点C作于点R,交线段于点K,再过点C作分别交边,于点P、Q,矩形的面积为3,矩形的面积为6,则的长为( )
A.4.5 B.5 C. D.
9.已知,那么下列等式中成立的是( )
A. B. C. D..
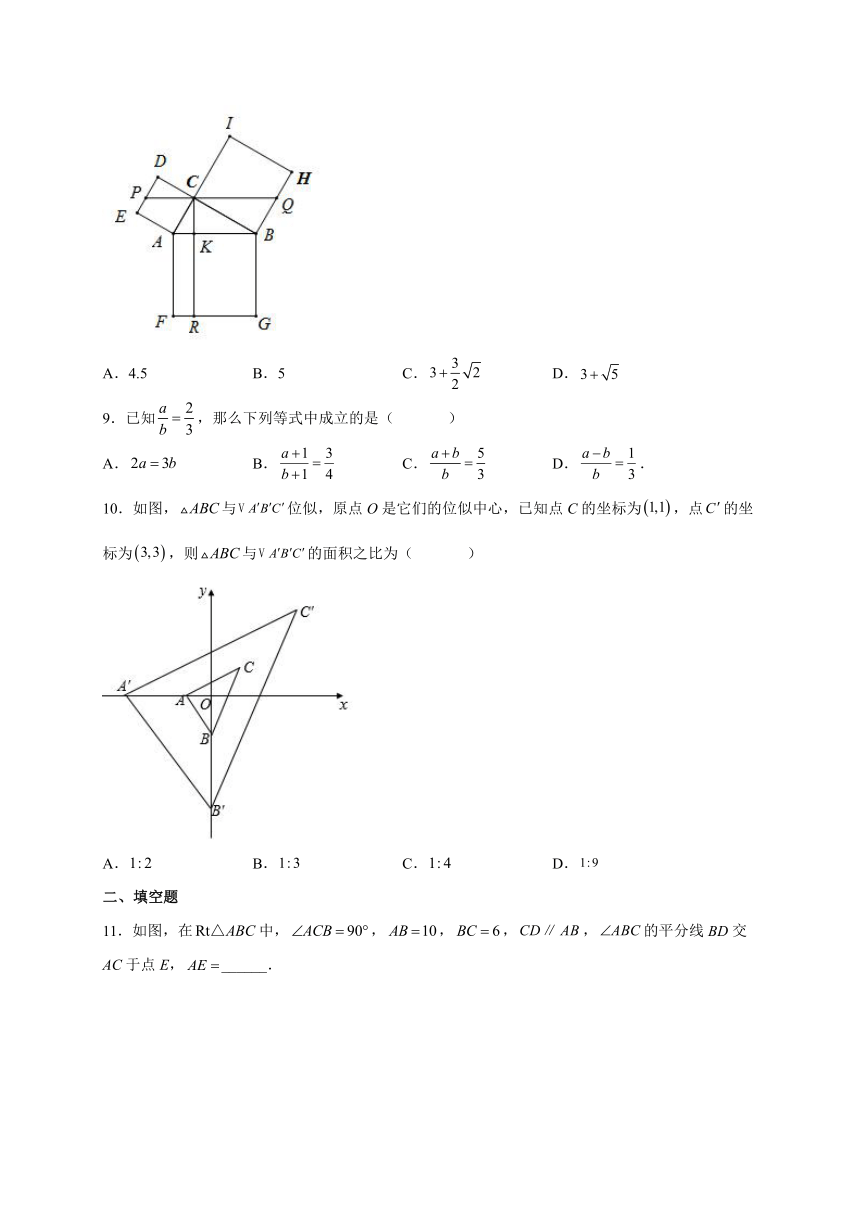
10.如图,与位似,原点O是它们的位似中心,已知点C的坐标为,点的坐标为,则与的面积之比为( )
A. B. C. D.
二、填空题
11.如图,在中,,,,,的平分线BD交AC于点E,______.
12.已知,那么(a﹣b):a=___.
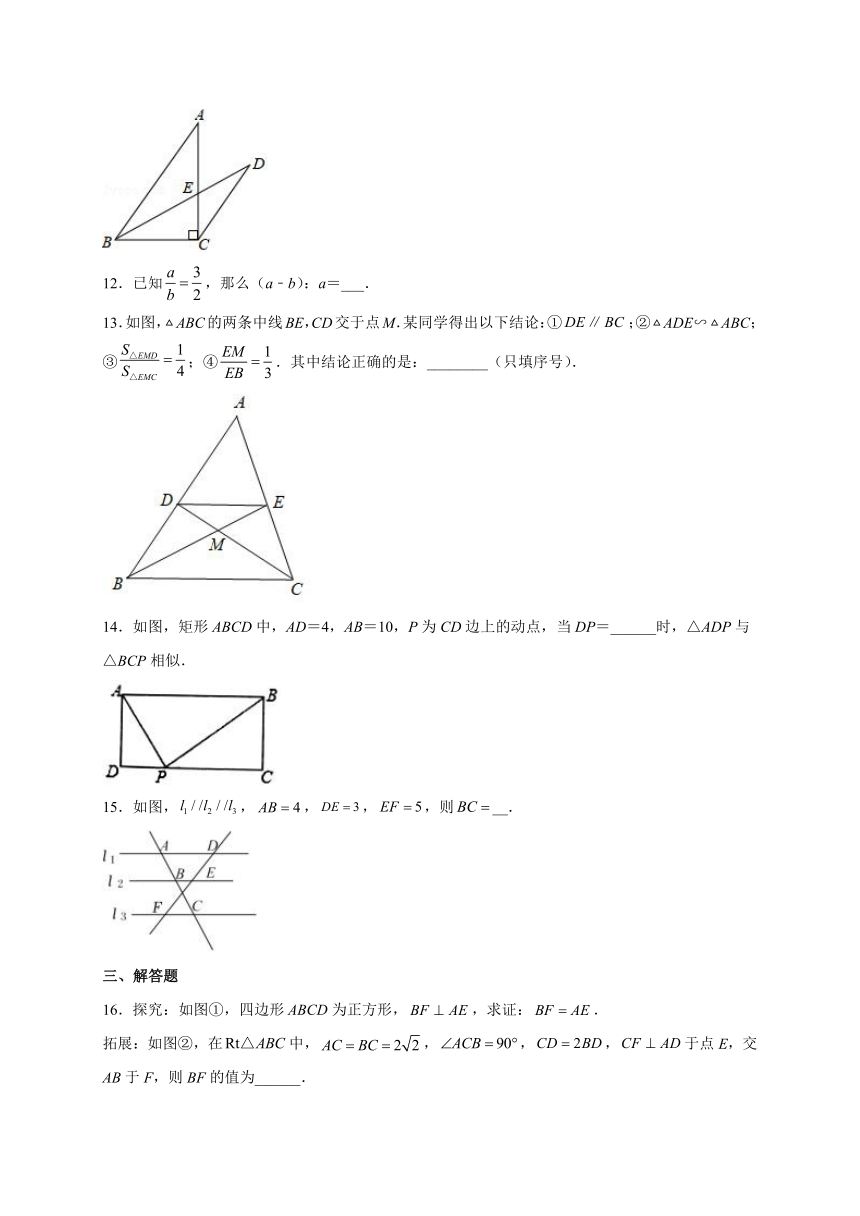
13.如图,ABC的两条中线BE,CD交于点M.某同学得出以下结论:①;②ADE∽ABC;③;④.其中结论正确的是:________(只填序号).
14.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=______时,△ADP与△BCP相似.
15.如图,,,,,则__.
三、解答题
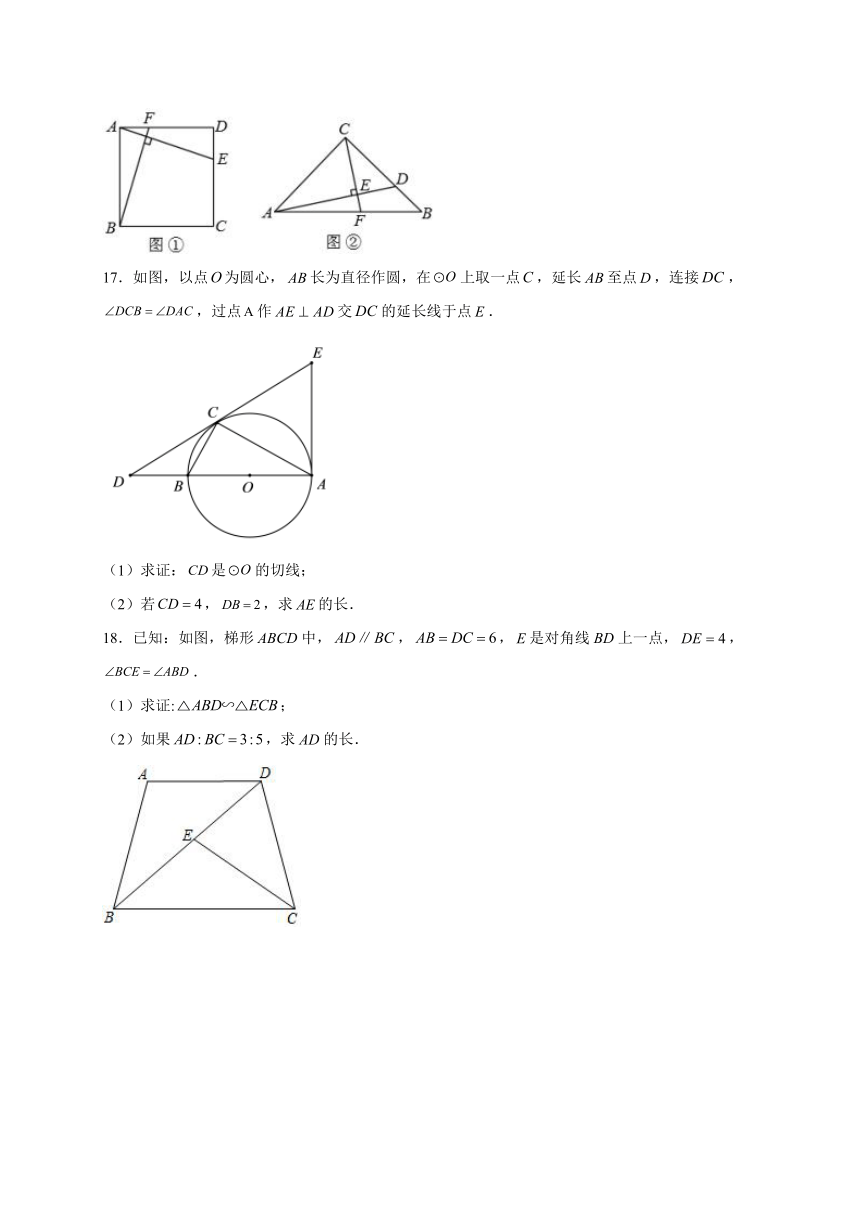
16.探究:如图①,四边形ABCD为正方形,,求证:.
拓展:如图②,在中,,,,于点E,交AB于F,则BF的值为______.
17.如图,以点为圆心,长为直径作圆,在上取一点,延长至点,连接,,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
18.已知:如图,梯形ABCD中,,,是对角线BD上一点,,.
(1)求证:;
(2)如果,求AD的长.
试卷第页,共页
参考答案:
1.B
【详解】
解:∵AE=2ED,AD=AE+DE=3DE,
∴ ,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD,
∴∠DEF=∠BCF,∠EDF=∠CBF,
,
,
∴,
,
.
故选:B.
2.A
【详解】
解:∵∠BAC=90°,AB=AC=4,
∴∠B=∠C=45°,BC==4.
∵∠ADE=45°,
∴∠ADE=∠C=45°.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴①正确;
∵∠ADE=45°,
∴∠ADB+∠EDC=180°﹣45°=135°.
∵∠B=45°,
∴∠ADB+∠BAD=180°45°=135°.
∴∠BAD=∠EDC.
∵∠B=∠C,
∴△ABD∽△DCE.
∴②正确;
由①知:△ADE∽△ACD,
∴.
∴AD2=AE AC.
∴.
∴.
∴③正确;
∵点D是边BC上一动点(不与B,C重合),
∴0<AD<4.
∵垂线段最短,
∴当AD⊥BC时,AD取得最小值=BC=2.
∴2≤AD<4.
∵AD2=AE AC,
∴AE==.
∴2≤AE<4.
∵EC=AC﹣AE=4﹣,
∴0<CE≤2.
∴④正确.
综上,正确的结论有:①②③④.
故选:A.
3.C
【详解】
∵BD=CD,ED⊥BC,ED=ED
∴△BDE≌△CDE(SAS),
∴EB=EC,∠ABC=∠ECB
又∵AD=AC,
∴∠ADC=∠ACD,
∴△ABC∽△FCD
∵BD=CD
∴△ABC∽△FCD相似比为2:1
∴AC:DF=2:1
∴AC=6,DF=3
故正确,共3个正确.
故选:C.
4.D
【详解】
∵A1B1∥A2B2
∴∠A1A2B1=∠A2A3B2
∵A2B1∥A3B2
∴∠A1A2B1=∠A2A3B2
∴ △A1A2B1∽△A2A3B2(AA)
同理可证△A2A3B2∽△A3A4B3,△A2B1B2∽△A3B2B3
∵△A2B1B2∽△A3B2B3,,
∴,
又∵△A1A2B1∽△A2A3B2
∴
设之间的距离为h,则:,
∴
又∵
∴
∴,
∵,△A1A2B1∽△A2A3B2
∴
∴,
同理有,
∴图中三个阴影三角形面积之和为:
,
故选:D.
5.B
【详解】
解:如图,设正方形网格中小方格的边长为1,
则有AB=1,BC=,AC=,DE=2,EF=,DF=,
∴,
∴△ABC∽△EDF,
∴S△ABC:S△DEF=,
故选:B.
6.B
【详解】
解:∵与是位似图形,且,
与的位似比是.
则周长:周长,
∵△ABC的周长为2,
∴周长
故选:B.
7.C
【详解】
A.2::,故四条线段不成比例,不符合题意,
B.::,故四条线段不成比例,不符合题意,
C.::,故四条线段成比例,符符合题意,
D.::,故四条线段不成比例,不符合题意.
故选:C.
8.C
【详解】
∵矩形的面积为3,矩形的面积为6,
∴正方形AFGB的面积为9,
∴AB=3,AK=1,BK=2,
∵∠CAB=∠KAC,∠ACB=∠AKC=90°,
∴△ACK∽△ABC,
∴,即,
解得:,
∴BC==,
∵,,四边形AFGB是正方形,
∴PQ//AB,
∵四边形CBHI是正方形,
∴AC//BQ,
∴四边形ABQC是平行四边形,
∴CQ=AB=3,∠PCD=∠ABC,
∵∠PDC=∠ACB=90°,
∴△PCD∽△ABC,
∴,
∵四边形EACD是正方形,
∴AC=CD,
∴,
解得:PC=,
∴PQ=PC+CQ=3+.
故选:C.
9.C
【详解】
解:∵a:b=2:3的两内项是b、2,两外项是a、3,
∴3a=2b,
A:由以上解释易知A选项错误,不符题意;
B:,即,故错误,不符题意;
C: ,即,故正确,符合题意;
D:,即3a=4b,故错误,不符题意;
故选C.
10.D
【详解】
∵与位似,原点O是它们的位似中心,点C的坐标为,点的坐标为
∴△ABC∽△A′B′C′,且相似比为,
∴,
故选:D.
11.5
【详解】
解:∵∠ACB=90°,AB=10,BC=6,
∴,
∵BD平分∠ABC,
∴∠ABE=∠CDE,
∵CD∥AB,
∴∠D=∠ABE,
∴∠D=∠CBE,
∴CD=BC=6,
∴△AEB∽△CED,
∴,
∴,
∴AE=5,
故答案为:5.
12.1:3
【详解】
解:∵
∴设,
∴(a﹣b):a=
故答案为:1:3
13.①②④
【详解】
解:∵BE是边AC上的中线,CD是AB边上的中线,
∴点E为AC边的中点,点D为AB边的中点,
∴DE为△ABC的中位线,
∴DE//BC,故结论①正确;
∴∠AED=∠ACB,∠ADE=∠ABC
∴△ADE∽△ABC,故结论②正确;
∵DE为△ABC的中位线,
∴DE//BC,DE=BC
∴
∴
∴,故③错误;
∵DE//BC
∴
∴
∴,故④正确;
∴正确的结论是①②④
故答案为:①②④
14.2或5或8
【详解】
∵四边形ABCD是矩形
∴BC=AD=4,CD=AB=10
当△ADP∽△PCB时,,即
∴DP(10 DP)=16
即
解得:DP=2或DP=8
当△ADP∽△BCP时,
∴DP=PC
∵DP+PC=10
∴DP=5
综上所述,当DP的长为2或5或8时,△ADP与△BCP相似.
故答案为:2或5或8
15.
【详解】
解:////,
,
,,,
,
解得:,
故答案为:.
16.探究:见解析,拓展:
【详解】
探究:证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠D=90°,
∴∠DAE+∠BAE=90°,
∵BF⊥AE,
∴∠ABF+∠BAE=90°,
∴∠ABF=∠DAE,
在△ABF和△ADE中,
,
∴△ABF≌△ADE(ASA),
∴BF=AE;
拓展:作BG⊥CB,交CF延长线于点G,
∵,
∴∠ACB=∠CBG=∠CED=90°,
∴∠G+∠GCB=90°,∠EDC+∠GCB=90°,BG∥CA;
∴∠G=∠EDC,
在△ACD和△CBG中,
,
∴△ACD≌△CBG(ASA),
∴BG=CD;
∵BG∥CA;
∴△BGF∽△ACF,
∴,
∵,,
∴,,
∴,
故答案为:
17.(1)证明见解析;(2).
【详解】
证明:(1)如图,连接,
是的直径,
,
,
,
,
,
,
,即,
又是的半径,
是的切线;
(2)设的半径为,则,
,
,
在中,,即,
解得,
,
在和中,,
,
,即,
解得.
18.(1)见解析;(2)
【详解】
解:(1)∵,
∴,
又∵,
∴.
(2)∵梯形ABCD中,,,
∴
又∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴
∵,
∴,
∵,
设,,
∴,
解得(舍去负值),
∴,即.
试卷第页,共页
试卷第1页,共1页
一、单选题
1.如图,在平行四边形ABCD中,点E是边AD上的一点,且AE=2ED,EC交对角线BD于点F,,则( )
A.6 B.18 C.4 D.9
2.如图,在△ABC中,∠BAC=90°,AB=AC=4,点D是边BC上一动点(不与B,C重合),∠ADE=45°,DE交AC于点E,下列结论:①△ADE与△ACD一定相似;②△ABD与△DCE一定相似;③当AD=3时,;④0<CE≤2.其中正确的结论有几个?( )
A.4个 B.3个 C.2个 D.1个
3.如图,△ADC中,AD=AC,延长CD至B,使BD=CD,ED⊥BC交AB于E,EC交AD于F,下列四个结论:①EB=EC;②△BDE∽△BAC;③△ABC∽△FCD;④若AC=6,则DF=3,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
4.如图,点A1,A2,A3,A4在射线OA上,点B1,B2,B3在射线OB上,且A1B1∥A2B2∥A3B3,A2B1∥A3B2∥A4B3.若△A2B1B2,△A3B2B3的面积分别为1,4,则图中三个阴影三角形面积之和为 ( )
A.8 B.9 C.10 D.10.5
5.如图所示的网格是正方形网格,A,B,C,D,E,F是网格线的交点,则△ABC的面积与△DEF的面积比为( )
A. B. C.2 D.4
6.如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
7.下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
8.如图,在中,,以其三边为边向外作正方形,过点C作于点R,交线段于点K,再过点C作分别交边,于点P、Q,矩形的面积为3,矩形的面积为6,则的长为( )
A.4.5 B.5 C. D.
9.已知,那么下列等式中成立的是( )
A. B. C. D..
10.如图,与位似,原点O是它们的位似中心,已知点C的坐标为,点的坐标为,则与的面积之比为( )
A. B. C. D.
二、填空题
11.如图,在中,,,,,的平分线BD交AC于点E,______.
12.已知,那么(a﹣b):a=___.
13.如图,ABC的两条中线BE,CD交于点M.某同学得出以下结论:①;②ADE∽ABC;③;④.其中结论正确的是:________(只填序号).
14.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=______时,△ADP与△BCP相似.
15.如图,,,,,则__.
三、解答题
16.探究:如图①,四边形ABCD为正方形,,求证:.
拓展:如图②,在中,,,,于点E,交AB于F,则BF的值为______.
17.如图,以点为圆心,长为直径作圆,在上取一点,延长至点,连接,,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
18.已知:如图,梯形ABCD中,,,是对角线BD上一点,,.
(1)求证:;
(2)如果,求AD的长.
试卷第页,共页
参考答案:
1.B
【详解】
解:∵AE=2ED,AD=AE+DE=3DE,
∴ ,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD,
∴∠DEF=∠BCF,∠EDF=∠CBF,
,
,
∴,
,
.
故选:B.
2.A
【详解】
解:∵∠BAC=90°,AB=AC=4,
∴∠B=∠C=45°,BC==4.
∵∠ADE=45°,
∴∠ADE=∠C=45°.
∵∠DAE=∠CAD,
∴△ADE∽△ACD.
∴①正确;
∵∠ADE=45°,
∴∠ADB+∠EDC=180°﹣45°=135°.
∵∠B=45°,
∴∠ADB+∠BAD=180°45°=135°.
∴∠BAD=∠EDC.
∵∠B=∠C,
∴△ABD∽△DCE.
∴②正确;
由①知:△ADE∽△ACD,
∴.
∴AD2=AE AC.
∴.
∴.
∴③正确;
∵点D是边BC上一动点(不与B,C重合),
∴0<AD<4.
∵垂线段最短,
∴当AD⊥BC时,AD取得最小值=BC=2.
∴2≤AD<4.
∵AD2=AE AC,
∴AE==.
∴2≤AE<4.
∵EC=AC﹣AE=4﹣,
∴0<CE≤2.
∴④正确.
综上,正确的结论有:①②③④.
故选:A.
3.C
【详解】
∵BD=CD,ED⊥BC,ED=ED
∴△BDE≌△CDE(SAS),
∴EB=EC,∠ABC=∠ECB
又∵AD=AC,
∴∠ADC=∠ACD,
∴△ABC∽△FCD
∵BD=CD
∴△ABC∽△FCD相似比为2:1
∴AC:DF=2:1
∴AC=6,DF=3
故正确,共3个正确.
故选:C.
4.D
【详解】
∵A1B1∥A2B2
∴∠A1A2B1=∠A2A3B2
∵A2B1∥A3B2
∴∠A1A2B1=∠A2A3B2
∴ △A1A2B1∽△A2A3B2(AA)
同理可证△A2A3B2∽△A3A4B3,△A2B1B2∽△A3B2B3
∵△A2B1B2∽△A3B2B3,,
∴,
又∵△A1A2B1∽△A2A3B2
∴
设之间的距离为h,则:,
∴
又∵
∴
∴,
∵,△A1A2B1∽△A2A3B2
∴
∴,
同理有,
∴图中三个阴影三角形面积之和为:
,
故选:D.
5.B
【详解】
解:如图,设正方形网格中小方格的边长为1,
则有AB=1,BC=,AC=,DE=2,EF=,DF=,
∴,
∴△ABC∽△EDF,
∴S△ABC:S△DEF=,
故选:B.
6.B
【详解】
解:∵与是位似图形,且,
与的位似比是.
则周长:周长,
∵△ABC的周长为2,
∴周长
故选:B.
7.C
【详解】
A.2::,故四条线段不成比例,不符合题意,
B.::,故四条线段不成比例,不符合题意,
C.::,故四条线段成比例,符符合题意,
D.::,故四条线段不成比例,不符合题意.
故选:C.
8.C
【详解】
∵矩形的面积为3,矩形的面积为6,
∴正方形AFGB的面积为9,
∴AB=3,AK=1,BK=2,
∵∠CAB=∠KAC,∠ACB=∠AKC=90°,
∴△ACK∽△ABC,
∴,即,
解得:,
∴BC==,
∵,,四边形AFGB是正方形,
∴PQ//AB,
∵四边形CBHI是正方形,
∴AC//BQ,
∴四边形ABQC是平行四边形,
∴CQ=AB=3,∠PCD=∠ABC,
∵∠PDC=∠ACB=90°,
∴△PCD∽△ABC,
∴,
∵四边形EACD是正方形,
∴AC=CD,
∴,
解得:PC=,
∴PQ=PC+CQ=3+.
故选:C.
9.C
【详解】
解:∵a:b=2:3的两内项是b、2,两外项是a、3,
∴3a=2b,
A:由以上解释易知A选项错误,不符题意;
B:,即,故错误,不符题意;
C: ,即,故正确,符合题意;
D:,即3a=4b,故错误,不符题意;
故选C.
10.D
【详解】
∵与位似,原点O是它们的位似中心,点C的坐标为,点的坐标为
∴△ABC∽△A′B′C′,且相似比为,
∴,
故选:D.
11.5
【详解】
解:∵∠ACB=90°,AB=10,BC=6,
∴,
∵BD平分∠ABC,
∴∠ABE=∠CDE,
∵CD∥AB,
∴∠D=∠ABE,
∴∠D=∠CBE,
∴CD=BC=6,
∴△AEB∽△CED,
∴,
∴,
∴AE=5,
故答案为:5.
12.1:3
【详解】
解:∵
∴设,
∴(a﹣b):a=
故答案为:1:3
13.①②④
【详解】
解:∵BE是边AC上的中线,CD是AB边上的中线,
∴点E为AC边的中点,点D为AB边的中点,
∴DE为△ABC的中位线,
∴DE//BC,故结论①正确;
∴∠AED=∠ACB,∠ADE=∠ABC
∴△ADE∽△ABC,故结论②正确;
∵DE为△ABC的中位线,
∴DE//BC,DE=BC
∴
∴
∴,故③错误;
∵DE//BC
∴
∴
∴,故④正确;
∴正确的结论是①②④
故答案为:①②④
14.2或5或8
【详解】
∵四边形ABCD是矩形
∴BC=AD=4,CD=AB=10
当△ADP∽△PCB时,,即
∴DP(10 DP)=16
即
解得:DP=2或DP=8
当△ADP∽△BCP时,
∴DP=PC
∵DP+PC=10
∴DP=5
综上所述,当DP的长为2或5或8时,△ADP与△BCP相似.
故答案为:2或5或8
15.
【详解】
解:////,
,
,,,
,
解得:,
故答案为:.
16.探究:见解析,拓展:
【详解】
探究:证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠D=90°,
∴∠DAE+∠BAE=90°,
∵BF⊥AE,
∴∠ABF+∠BAE=90°,
∴∠ABF=∠DAE,
在△ABF和△ADE中,
,
∴△ABF≌△ADE(ASA),
∴BF=AE;
拓展:作BG⊥CB,交CF延长线于点G,
∵,
∴∠ACB=∠CBG=∠CED=90°,
∴∠G+∠GCB=90°,∠EDC+∠GCB=90°,BG∥CA;
∴∠G=∠EDC,
在△ACD和△CBG中,
,
∴△ACD≌△CBG(ASA),
∴BG=CD;
∵BG∥CA;
∴△BGF∽△ACF,
∴,
∵,,
∴,,
∴,
故答案为:
17.(1)证明见解析;(2).
【详解】
证明:(1)如图,连接,
是的直径,
,
,
,
,
,
,
,即,
又是的半径,
是的切线;
(2)设的半径为,则,
,
,
在中,,即,
解得,
,
在和中,,
,
,即,
解得.
18.(1)见解析;(2)
【详解】
解:(1)∵,
∴,
又∵,
∴.
(2)∵梯形ABCD中,,,
∴
又∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴
∵,
∴,
∵,
设,,
∴,
解得(舍去负值),
∴,即.
试卷第页,共页
试卷第1页,共1页
