2022年人教版九年级数学下册第二十七章 相似(一) 单元测试(Word版含答案)
文档属性
| 名称 | 2022年人教版九年级数学下册第二十七章 相似(一) 单元测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 733.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 18:02:08 | ||
图片预览

文档简介
初中数学九年级下册相似模拟试题(一)
一、单选题
1.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
2.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C.AC2=AD AB D.BC2=BD AB
3.下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
4.如图,点在线段上,在的同侧作等腰直角三角形和等腰直角三角形,与、分别交于点,,给出下列结论:①;②;③;其中所有正确的结论序号为( )
A.① B.①② C.①②③ D.②③
5.如图,Rt△ABC中,∠A=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,若AB=4,BE=,则AD长是( )
A.2 B.3 C. D.
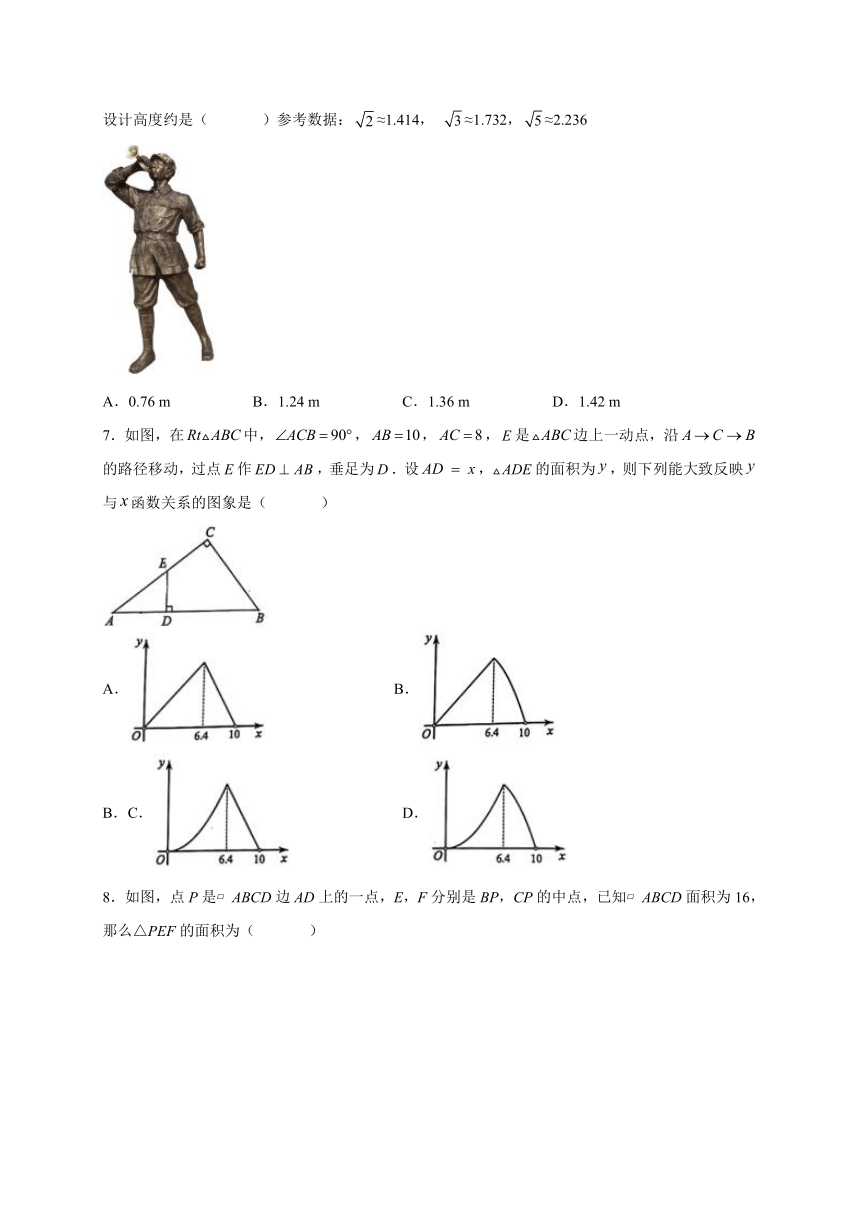
6.在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度约是( )参考数据:≈1.414, ≈1.732,≈2.236
A.0.76 m B.1.24 m C.1.36 m D.1.42 m
7.如图,在中,,,,是边上一动点,沿的路径移动,过点作,垂足为.设,的面积为,则下列能大致反映与函数关系的图象是( )
B.
C. D.
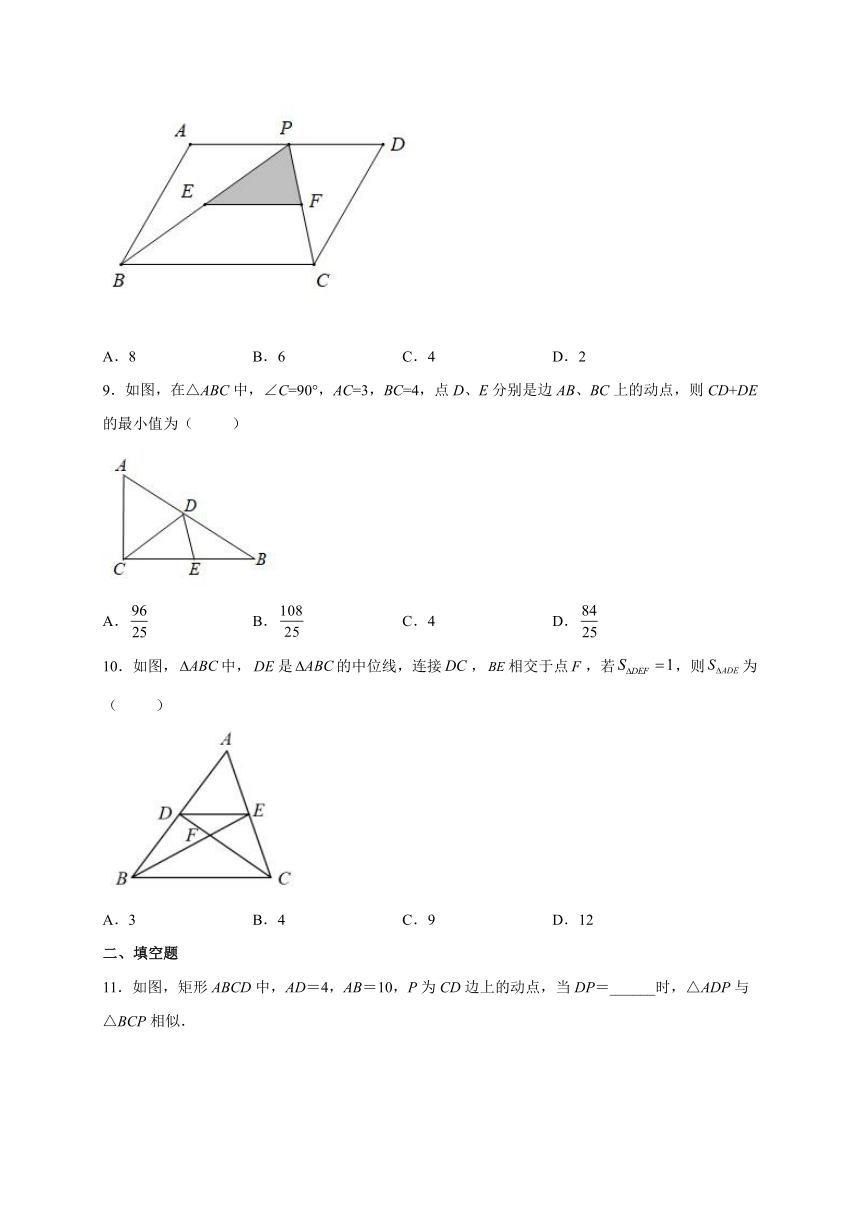
8.如图,点P是 ABCD边AD上的一点,E,F分别是BP,CP的中点,已知 ABCD面积为16,那么△PEF的面积为( )
A.8 B.6 C.4 D.2
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,点D、E分别是边AB、BC上的动点,则CD+DE的最小值为( )
A. B. C.4 D.
10.如图,中,是的中位线,连接,相交于点,若,则为( )
A.3 B.4 C.9 D.12
二、填空题
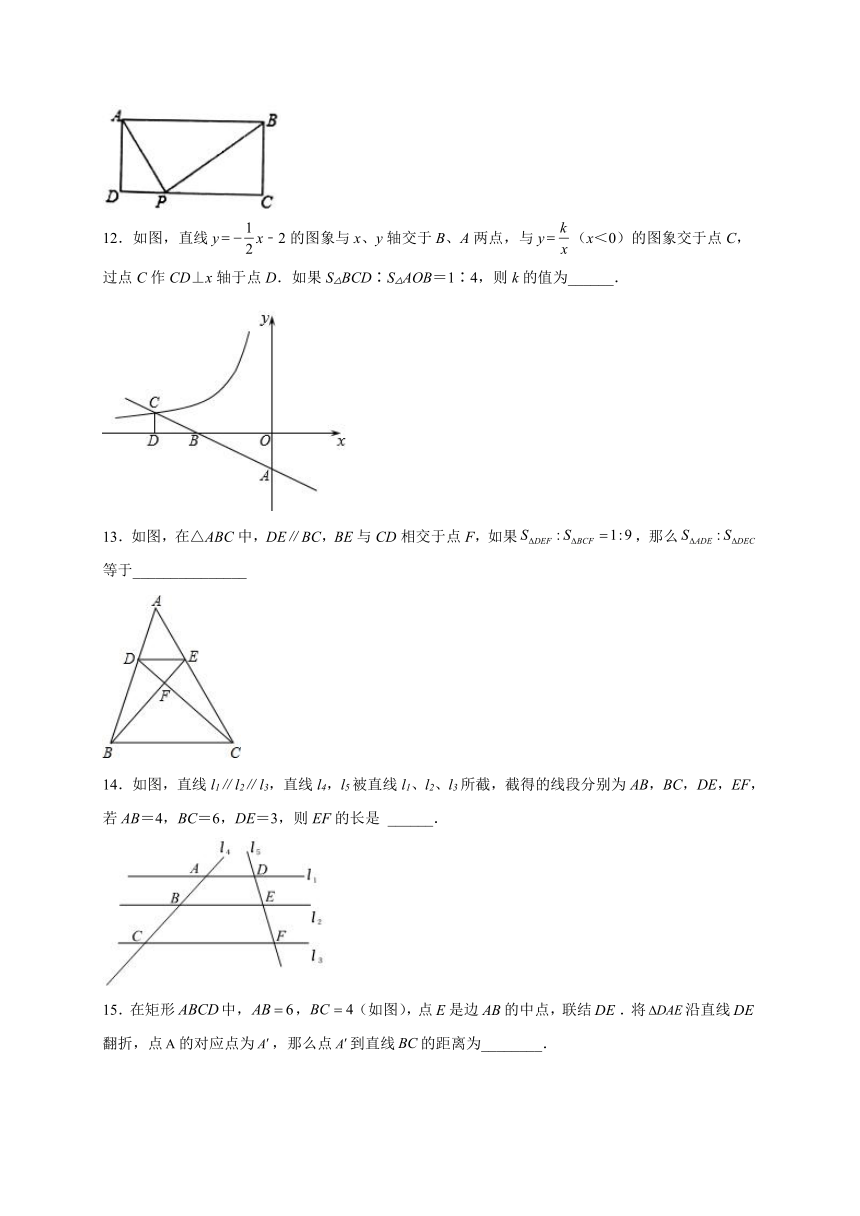
11.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=______时,△ADP与△BCP相似.
12.如图,直线yx﹣2的图象与x、y轴交于B、A两点,与y(x<0)的图象交于点C,过点C作CD⊥x轴于点D.如果S△BCD∶S△AOB=1∶4,则k的值为______.
13.如图,在△ABC中,DE∥BC,BE与CD相交于点F,如果,那么等于_______________
14.如图,直线l1∥l2∥l3,直线l4,l5被直线l1、l2、l3所截,截得的线段分别为AB,BC,DE,EF,若AB=4,BC=6,DE=3,则EF的长是 ______.
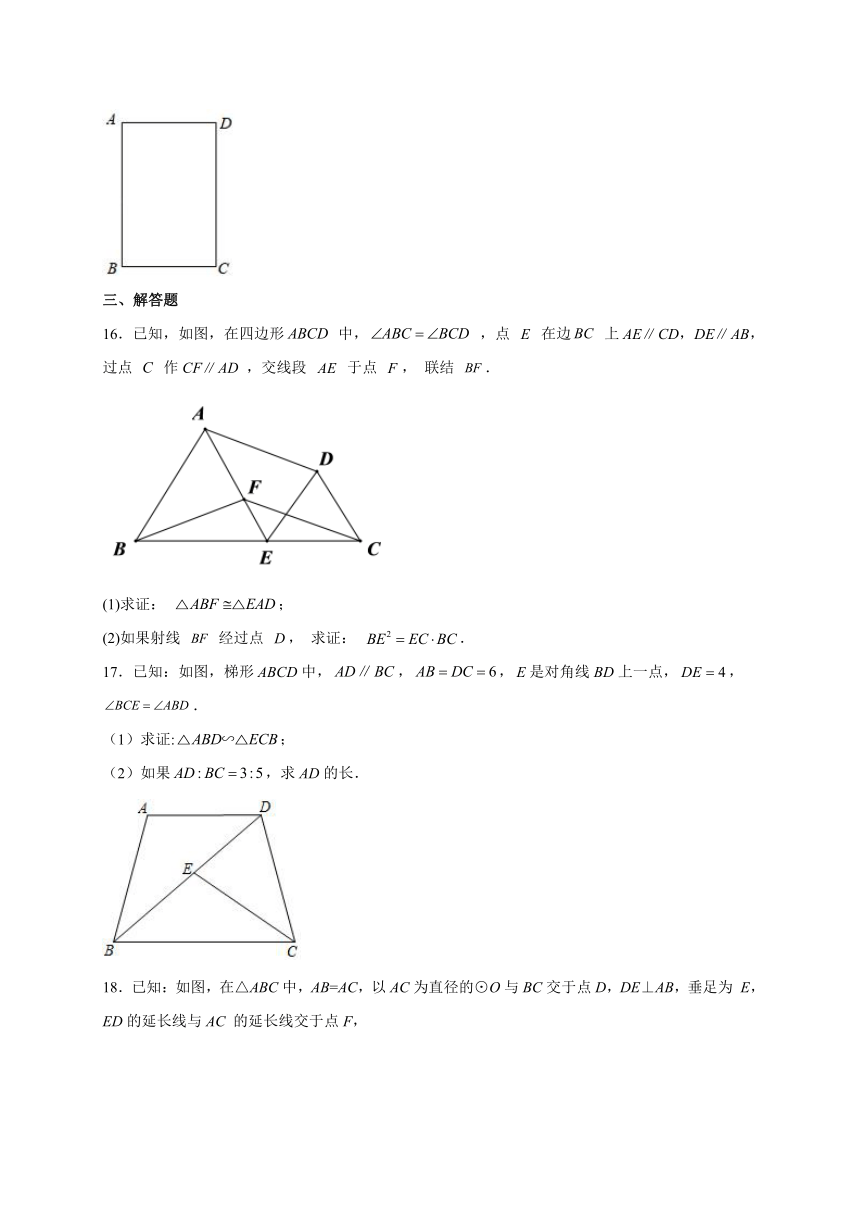
15.在矩形中,,(如图),点是边的中点,联结.将沿直线翻折,点的对应点为,那么点到直线的距离为________.
三、解答题
16.已知,如图,在四边形 中, ,点 在边 上AECD,DEAB, 过点 作CFAD ,交线段 于点 , 联结 .
(1)求证: ;
(2)如果射线 经过点 , 求证: .
17.已知:如图,梯形ABCD中,,,是对角线BD上一点,,.
(1)求证:;
(2)如果,求AD的长.
18.已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为 E,ED的延长线与AC 的延长线交于点F,
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,∠F =30°,求DE的长.
试卷第页,共页
参考答案:
1.A
【详解】
解:∵两个相似三角形的周长比为1:4,
∴两个相似三角形的相似比为1:4,
∴它们的对应角平分线之比为1:4,
故选:A.
2.D
【详解】
解:A.∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,故本选项不符合题意;
B.∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
C.∵AC2=AD AB,
∴,
∵∠A=∠A,
∴△ACD∽△ABC,故本选项不符合题意;
D.∵BC2=BD AB,
∴,
添加∠A=∠A,不能推出△ACD∽△ABC,故本选项符合题意.
故选:D
3.C
【详解】
A.2::,故四条线段不成比例,不符合题意,
B.::,故四条线段不成比例,不符合题意,
C.::,故四条线段成比例,符符合题意,
D.::,故四条线段不成比例,不符合题意.
故选:C.
4.C
【详解】
解:∵三角形和三角形都是等腰直角三角形,
∴AC=AB,AD=AE,
∴,
∵∠BAC=∠EAD,
∴∠BAE=∠CAD,
∴△BAE∽△CAD,
所以①正确;
∵△BAE∽△CAD,
∴∠BEA=∠CDA,
∵∠PME=∠AMD,
∴△PME∽△AMD,
∴,
∵∠PMA=∠DME,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°,故②正确,
∵∠CAE=180° ∠BAC ∠EAD=90°,
∴△CAP∽△CMA,
∴
∴AC2=CP CM,
∵AC=BC,
∴2CB2=CP CM,
所以③正确;
故选:C.
5.D
【详解】
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠B=∠C=45°,
∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,
∴∠BAE=∠CED
∴△ABE∽△ECD
∴
又∵AB=4,BE=,
∴,即
∴,
∴
故选D.
6.B
【详解】
解:如图,由题意得:
设该雕像的下部设计高度为:m,
则
解得:
经检验:不符合题意;
故选B
7.D
【详解】
解:∵,,,
∴BC=,
过CA点作CH⊥AB于H,
∴∠ADE=∠ACB=90°,
∵,
∴CH=4.8,
∴AH=,
当0≤x≤6.4时,如图1,
∵∠A=∠A,∠ADE=∠ACB=90°,
∴△ADE∽△ACB,
∴,即,解得:x=,
∴y= x =x2;
当6.4<x≤10时,如图2,
∵∠B=∠B,∠BDE=∠ACB=90°,
∴△BDE∽△BCA,
∴,
即,解得:x=,
∴y= x =;
故选:D.
8.D
【详解】
∵点P是 ABCD边AD上的一点,且 ABCD面积为16,
∴;
∵E,F分别是BP,CP的中点,
∴EF∥BC,EF=,
∴△PEF∽△PBC,
∴,
∴,
故选D.
9.A
【详解】
解:作点C关于AB的对称点F,过点F作FG⊥BC于G,交AB于点D,如图:
∴DC=DF,
则CD+DE的最小值为FG的长;
∵点C、点F关于AB的对称,
∴CF⊥AB,CH=HF,
AB=5,
∵,
∴CH=,
∴CF=,BH=,
∵∠FCB+∠F=∠FCB+∠B=90°,
∴∠F=∠B,
∴Rt△FGCRt△BHC,
∴,即,
∴FG=,
故选:A.
10.A
【详解】
∵是的中位线,
∴DE∥BC,BC=2DE,
∴△DEF∽△CBF,
∴,
∴,
∵,
∴,
∵BE是中线,
∴=,
∵是的中位线,
∴DE∥BC,
∴=,
∴=,
∴++=+,
∴+=,
∴=3,
故选A.
11.2或5或8
【详解】
∵四边形ABCD是矩形
∴BC=AD=4,CD=AB=10
当△ADP∽△PCB时,,即
∴DP(10 DP)=16
即
解得:DP=2或DP=8
当△ADP∽△BCP时,
∴DP=PC
∵DP+PC=10
∴DP=5
综上所述,当DP的长为2或5或8时,△ADP与△BCP相似.
故答案为:2或5或8
12.
【详解】
解: 直线yx﹣2的图象与x、y轴交于B、A两点,
令 则 令 则
CD⊥x轴于点D,
轴,
而S△BCD∶S△AOB=1∶4,
故答案为:
13.
【详解】
解:,
,
,
,
分别过点作的垂线,交于,
在与,
,
,
,
,
故答案是:.
14.4.5
【详解】
解:∵l1//l2//l3,
∴,
∵AB=4,BC=6,DE=3,
∴,
解得:EF=4.5,
故答案为:4.5.
15.####2.16
【详解】
解:过作交于,交于,过作于,如图:
矩形中,,,是边的中点
,,,,
沿直线翻折,点的对应点为,
,,,
又,
,
而,
△,
,
设,,则,,
,,
,
解得,
,
,
∴,
故答案为:.
16.
(1)
证明:∵,
∴,,
∴,即,
∴.
∵,
∴,,
∴,即,
∴.
又∵,
∴四边形AFCD为平行四边形,
∴,
∴,
∴在和中,,
∴.
(2)
证明:如图,连接DF.
∵射线 BF 经过点 D,
∴点B、F、D共线.
∵,即,
∴,
∴.
∵,
∴,
∴,
∴.
∵AF=CD,
∴,
∴,
∴.
17.(1)见解析;(2)
【详解】
解:(1)∵,
∴,
又∵,
∴.
(2)∵梯形ABCD中,,,
∴
又∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴
∵,
∴,
∵,
设,,
∴,
解得(舍去负值),
∴,即.
18.(1)见解析
(2)
(1)
证明:连接AD、OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AC是⊙O的直径,
∴∠ADC=90°即AD⊥BC,又AB=AC,
∴∠BAD=∠OAD,
∴∠EAD=∠ODA,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,又OD是半径,
∴DE是⊙O的切线;
(2)
解:在Rt△ODF中,OD=4,∠F=30°,
∴OF=2OD=8,DF= OD= ,
∵OD∥AB,
∴即,
∴.
试卷第页,共页
试卷第1页,共1页
一、单选题
1.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
2.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.∠ACD=∠B B.∠ADC=∠ACB C.AC2=AD AB D.BC2=BD AB
3.下列各组长度的线段(单位:cm)中,成比例线段的是( )
A.,,, B.,,, C.,,, D.,,,
4.如图,点在线段上,在的同侧作等腰直角三角形和等腰直角三角形,与、分别交于点,,给出下列结论:①;②;③;其中所有正确的结论序号为( )
A.① B.①② C.①②③ D.②③
5.如图,Rt△ABC中,∠A=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,若AB=4,BE=,则AD长是( )
A.2 B.3 C. D.
6.在设计人体雕像时,使雕像上部(腰部以上)与下部(腰部以下)的高度比,等于下部与全部的高度比,可以增加视觉美感.如图,按此比例设计一座高度为2 m的雷锋雕像,那么该雕像的下部设计高度约是( )参考数据:≈1.414, ≈1.732,≈2.236
A.0.76 m B.1.24 m C.1.36 m D.1.42 m
7.如图,在中,,,,是边上一动点,沿的路径移动,过点作,垂足为.设,的面积为,则下列能大致反映与函数关系的图象是( )
B.
C. D.
8.如图,点P是 ABCD边AD上的一点,E,F分别是BP,CP的中点,已知 ABCD面积为16,那么△PEF的面积为( )
A.8 B.6 C.4 D.2
9.如图,在△ABC中,∠C=90°,AC=3,BC=4,点D、E分别是边AB、BC上的动点,则CD+DE的最小值为( )
A. B. C.4 D.
10.如图,中,是的中位线,连接,相交于点,若,则为( )
A.3 B.4 C.9 D.12
二、填空题
11.如图,矩形ABCD中,AD=4,AB=10,P为CD边上的动点,当DP=______时,△ADP与△BCP相似.
12.如图,直线yx﹣2的图象与x、y轴交于B、A两点,与y(x<0)的图象交于点C,过点C作CD⊥x轴于点D.如果S△BCD∶S△AOB=1∶4,则k的值为______.
13.如图,在△ABC中,DE∥BC,BE与CD相交于点F,如果,那么等于_______________
14.如图,直线l1∥l2∥l3,直线l4,l5被直线l1、l2、l3所截,截得的线段分别为AB,BC,DE,EF,若AB=4,BC=6,DE=3,则EF的长是 ______.
15.在矩形中,,(如图),点是边的中点,联结.将沿直线翻折,点的对应点为,那么点到直线的距离为________.
三、解答题
16.已知,如图,在四边形 中, ,点 在边 上AECD,DEAB, 过点 作CFAD ,交线段 于点 , 联结 .
(1)求证: ;
(2)如果射线 经过点 , 求证: .
17.已知:如图,梯形ABCD中,,,是对角线BD上一点,,.
(1)求证:;
(2)如果,求AD的长.
18.已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为 E,ED的延长线与AC 的延长线交于点F,
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,∠F =30°,求DE的长.
试卷第页,共页
参考答案:
1.A
【详解】
解:∵两个相似三角形的周长比为1:4,
∴两个相似三角形的相似比为1:4,
∴它们的对应角平分线之比为1:4,
故选:A.
2.D
【详解】
解:A.∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,故本选项不符合题意;
B.∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
C.∵AC2=AD AB,
∴,
∵∠A=∠A,
∴△ACD∽△ABC,故本选项不符合题意;
D.∵BC2=BD AB,
∴,
添加∠A=∠A,不能推出△ACD∽△ABC,故本选项符合题意.
故选:D
3.C
【详解】
A.2::,故四条线段不成比例,不符合题意,
B.::,故四条线段不成比例,不符合题意,
C.::,故四条线段成比例,符符合题意,
D.::,故四条线段不成比例,不符合题意.
故选:C.
4.C
【详解】
解:∵三角形和三角形都是等腰直角三角形,
∴AC=AB,AD=AE,
∴,
∵∠BAC=∠EAD,
∴∠BAE=∠CAD,
∴△BAE∽△CAD,
所以①正确;
∵△BAE∽△CAD,
∴∠BEA=∠CDA,
∵∠PME=∠AMD,
∴△PME∽△AMD,
∴,
∵∠PMA=∠DME,
∴△PMA∽△EMD,
∴∠APD=∠AED=90°,故②正确,
∵∠CAE=180° ∠BAC ∠EAD=90°,
∴△CAP∽△CMA,
∴
∴AC2=CP CM,
∵AC=BC,
∴2CB2=CP CM,
所以③正确;
故选:C.
5.D
【详解】
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠B=∠C=45°,
∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,
∴∠BAE=∠CED
∴△ABE∽△ECD
∴
又∵AB=4,BE=,
∴,即
∴,
∴
故选D.
6.B
【详解】
解:如图,由题意得:
设该雕像的下部设计高度为:m,
则
解得:
经检验:不符合题意;
故选B
7.D
【详解】
解:∵,,,
∴BC=,
过CA点作CH⊥AB于H,
∴∠ADE=∠ACB=90°,
∵,
∴CH=4.8,
∴AH=,
当0≤x≤6.4时,如图1,
∵∠A=∠A,∠ADE=∠ACB=90°,
∴△ADE∽△ACB,
∴,即,解得:x=,
∴y= x =x2;
当6.4<x≤10时,如图2,
∵∠B=∠B,∠BDE=∠ACB=90°,
∴△BDE∽△BCA,
∴,
即,解得:x=,
∴y= x =;
故选:D.
8.D
【详解】
∵点P是 ABCD边AD上的一点,且 ABCD面积为16,
∴;
∵E,F分别是BP,CP的中点,
∴EF∥BC,EF=,
∴△PEF∽△PBC,
∴,
∴,
故选D.
9.A
【详解】
解:作点C关于AB的对称点F,过点F作FG⊥BC于G,交AB于点D,如图:
∴DC=DF,
则CD+DE的最小值为FG的长;
∵点C、点F关于AB的对称,
∴CF⊥AB,CH=HF,
AB=5,
∵,
∴CH=,
∴CF=,BH=,
∵∠FCB+∠F=∠FCB+∠B=90°,
∴∠F=∠B,
∴Rt△FGCRt△BHC,
∴,即,
∴FG=,
故选:A.
10.A
【详解】
∵是的中位线,
∴DE∥BC,BC=2DE,
∴△DEF∽△CBF,
∴,
∴,
∵,
∴,
∵BE是中线,
∴=,
∵是的中位线,
∴DE∥BC,
∴=,
∴=,
∴++=+,
∴+=,
∴=3,
故选A.
11.2或5或8
【详解】
∵四边形ABCD是矩形
∴BC=AD=4,CD=AB=10
当△ADP∽△PCB时,,即
∴DP(10 DP)=16
即
解得:DP=2或DP=8
当△ADP∽△BCP时,
∴DP=PC
∵DP+PC=10
∴DP=5
综上所述,当DP的长为2或5或8时,△ADP与△BCP相似.
故答案为:2或5或8
12.
【详解】
解: 直线yx﹣2的图象与x、y轴交于B、A两点,
令 则 令 则
CD⊥x轴于点D,
轴,
而S△BCD∶S△AOB=1∶4,
故答案为:
13.
【详解】
解:,
,
,
,
分别过点作的垂线,交于,
在与,
,
,
,
,
故答案是:.
14.4.5
【详解】
解:∵l1//l2//l3,
∴,
∵AB=4,BC=6,DE=3,
∴,
解得:EF=4.5,
故答案为:4.5.
15.####2.16
【详解】
解:过作交于,交于,过作于,如图:
矩形中,,,是边的中点
,,,,
沿直线翻折,点的对应点为,
,,,
又,
,
而,
△,
,
设,,则,,
,,
,
解得,
,
,
∴,
故答案为:.
16.
(1)
证明:∵,
∴,,
∴,即,
∴.
∵,
∴,,
∴,即,
∴.
又∵,
∴四边形AFCD为平行四边形,
∴,
∴,
∴在和中,,
∴.
(2)
证明:如图,连接DF.
∵射线 BF 经过点 D,
∴点B、F、D共线.
∵,即,
∴,
∴.
∵,
∴,
∴,
∴.
∵AF=CD,
∴,
∴,
∴.
17.(1)见解析;(2)
【详解】
解:(1)∵,
∴,
又∵,
∴.
(2)∵梯形ABCD中,,,
∴
又∵,
∴,
∵,
∴.
∴,
∵,,
∴,
∴
∵,
∴,
∵,
设,,
∴,
解得(舍去负值),
∴,即.
18.(1)见解析
(2)
(1)
证明:连接AD、OD,
∵OA=OD,
∴∠OAD=∠ODA,
∵AC是⊙O的直径,
∴∠ADC=90°即AD⊥BC,又AB=AC,
∴∠BAD=∠OAD,
∴∠EAD=∠ODA,
∴OD∥AB,
∵DE⊥AB,
∴OD⊥DE,又OD是半径,
∴DE是⊙O的切线;
(2)
解:在Rt△ODF中,OD=4,∠F=30°,
∴OF=2OD=8,DF= OD= ,
∵OD∥AB,
∴即,
∴.
试卷第页,共页
试卷第1页,共1页
