冀教版数学七下10.2 不等式的基本性质 课件(共46张PPT)
文档属性
| 名称 | 冀教版数学七下10.2 不等式的基本性质 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1005.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 19:47:20 | ||
图片预览









文档简介
(共46张PPT)
10.2 不等式的性质
第十章 一元一次不等式和一元一次不等式组
课时导入
请同学们回顾等式的基本性质:
1. 等式两边同时加上(或减去)同一个代数式,等式仍然
成立.
2. 等式两边同时乘同一个数(或除以同一个不为0的数),
等式仍然成立.
知识回顾
课时导入
利用等式的基本性质可以解方程.类似地,利用不
等式的基本性质 也可以解不等式.那么,不等式具有什
么性质呢?
导入新知
知识点
不等式的基本性质1
知1-讲
感悟新知
1
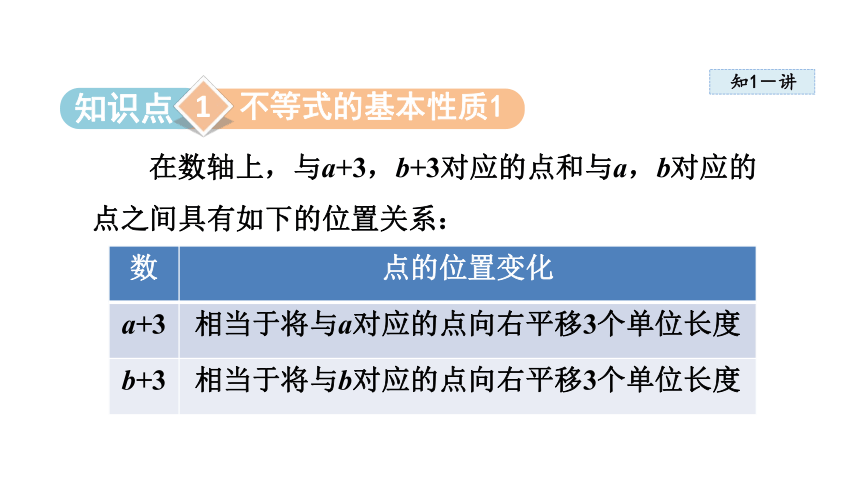
在数轴上,与a+3,b+3对应的点和与a,b对应的
点之间具有如下的位置关系:
数 点的位置变化
a+3 相当于将与a对应的点向右平移3个单位长度
b+3 相当于将与b对应的点向右平移3个单位长度
知1-讲
感悟新知
(1)确定a+3和b+3的大小.
(2)如果c>0,那么对于a+c和b+c的大小,你有什
么猜想?
(3)在不等式a>b的两边都减去同一个数或同一个整
式,你认为应该有什么结论
知1-讲
总 结
感悟新知
不等式两边都加上(或减去)同一个数或同一个整
式,不等号的方向不变.即
不等式的基本性质 1
如果a>b,那么a±c>b±c.
感悟新知
知1-练
例 1
分析:
从变形来看,是利用了不等式的基本性质1.
(1)根据不等式基本性质1,不等式两边同时减去6;
(2)根据不等式基本性质1,不等式两边同时减去6x.
指出下列不等式是如何变形的,并说明其变形的依据.
(1)若6+y>-7,则y>-13;
(2)若7x<6x+3,则x<3.
解:
知1-讲
总 结
感悟新知
判断某个不等式变形的根据:
一看不等号的方向是不是改变,二看式子的变化情况.
感悟新知
知1-练
1.
已知a<b,请用“>”或“<”填空:
(1)a-2_____b-2; (2) a+c_____b+c.
已知a>b,请用“>”或“<”填空:
(3)a+ _____b+ ;(4)a-6_____b-6.
<
<
>
>
感悟新知
知1-练
2.
把下列不等式化为“x>a”或“x<a”的形式:
(1)x+3<-2; (2)x-5<9.
(1)x+3<-2,
x+3-3<-2-3(不等式的基本性质1),
x<-5.
(2)x-5<9,x-5+5<9+5,所以x<14.
解:
感悟新知
知1-练
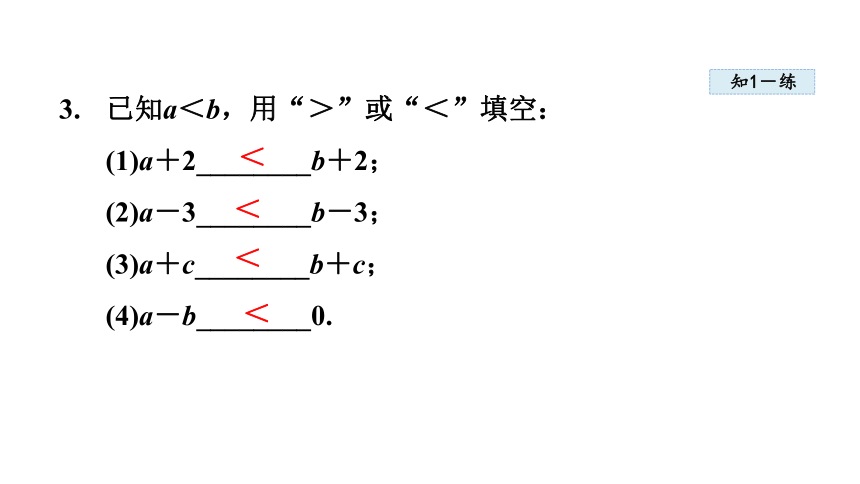
3.
已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
感悟新知
知1-练
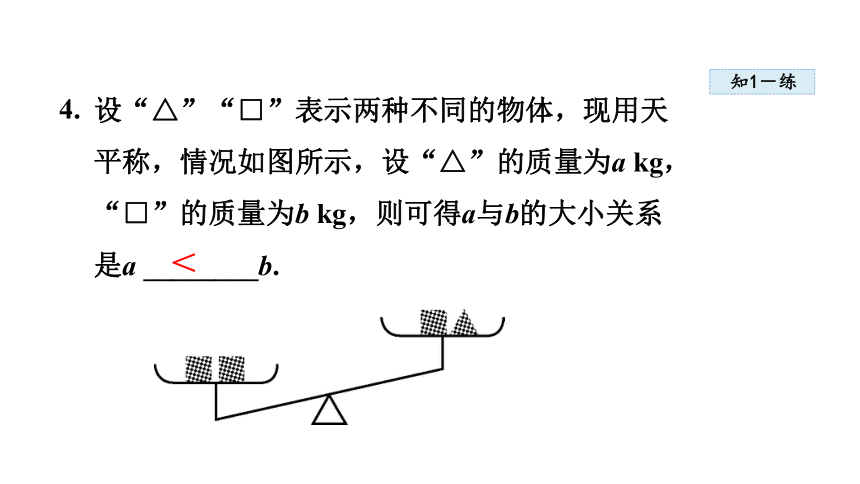
4.
设“△”“□”表示两种不同的物体,现用天平称,情况如图所示,设“△”的质量为a kg,“□”的质量为b kg,则可得a与b的大小关系是a ________b.
<
感悟新知
知1-练
5.
下列推理正确的是( )
A.因为a<b,所以a+2<b+1
B.因为a<b,所以a-1<b-2
C.因为a>b,所以a+c>b+c
D.因为a>b,所以a+c>b-d
C
感悟新知
知1-练
6.
由a-3<b+1,可得到结论( )
A.a<b
B.a+3<b-1
C.a-1<b+3
D.a+1<b-3
C
不等式的基本性质2
知识点
知2-讲
感悟新知
2
比较大小
由此我们可以得到:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
(-16)__(- 24);
(-16)×4__(- 24)×4;
(-16)÷3__(-24)÷3
8__12;
8×4__12×4;
8÷3__12÷3
知2-讲
总 结
感悟新知
不等式的两边都乘以(或除以)同一个正数,不等号的
方向不变.即
不等式的基本性质 2
如果 a>b,且c>0,那么ac>bc.
感悟新知
知2-练
例2
导引:
已知实数a、b ,若a>b ,则下列结论正确的
是( )
A.a-5<b-5 B.2+a<2+b
C. D.3a>3b
D
不等式的两边同时加上或减去一个数,不等号的方
向不变,不等式的两边同时除以或乘以一个正数,
不等号的方向也不变,所以A、B、C错误,选D.
知2-讲
总 结
感悟新知
在应用不等式的基本性质2时,除了注意“两同”
要求外,还要注意“正数”的要求;另外,乘除运
算可以灵活选择.
感悟新知
知2-练
1.
已知a<b,请用“>”或“<”填空:
(1)3a_____3b;
已知a>b,请用“>”或“<”填空:
(2)4a_____4b;(3) _____ .
<
>
>
2.
感悟新知
知2-练
解:
把下列不等式化为“x>a”或“x<a”的形式:
(1)9x>8x+1; (2) x>-4;
(3)6x<4x-2; (4) x>x+4.
(1)9x>8x+1,
9x-8x>8x+1-8x(不等式的基本性质1),x>1.
(2) x>-4,
2× x>2×(-4)(不等式的基本性质2),x>-8.
感悟新知
知2-练
(3)6x<4x-2,6x-4x<4x-2-4x,2x<-2,
2x÷2<(-2)÷2,所以x<-1.
(4) x>x+4, x-x>x+4-x, x>4,
x× >4× ,所以x>6.
3.
感悟新知
知2-练
若x>y,则4x-3________4y-3.(填“>”“<”或“=”)
由3a<4b,两边____________________,可变形为
a< b.
>
同乘 (或同除以12)
4.
5.
感悟新知
知2-练
m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C. > D.m2<n2
D
6.
感悟新知
知2-练
若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
A
7.
感悟新知
知2-练
当0<x<1时,x2,x, 的大小顺序是( )
A.x2C. A
不等式的基本性质3
知识点
知3-讲
感悟新知
3
1. 如果a>b,那么它们的相反数-a与-b哪个大,
你能用数轴上点的位置关系和具体的例子加以说
明吗?
2. 如果a>b ,那么-a<-b,这个式子可理解为:
a×(-1)<b×(-1)
这样,对于不等式a>b,两边同乘以-3,会
得到什么结果呢?
知3-讲
感悟新知
a>b a×(-1)<b×(-1) a×(-3)<b×(-3).
×(-1)
×3
×(-3)
3. 如果a>b,c<0,那么ac与bc有怎样的大小关系?
知3-讲
总 结
感悟新知
不等式两边都乘(或除以)同一个负数,不等号的方向
改变.即
不等式的基本性质 3
如果 a>b,且c<0,那么ac<bc.
知3-讲
感悟新知
特别解读
1. 不等式的三条基本性质是不等式变形的依据,运用
不等式的基本性质时,不等式的两边要同时进行相同的变形 .
2. 在不等式的变形中,还常用到性质:
(1)对称性:若 a>b, 则 b(2)传递性:若 a>b, b>c,则 a>b
感悟新知
知3-练
例 3
根据不等式的基本性质,把下列不等式化为“x>a”或“x<a”的形式:
(1)x-1>2; (2)2x<x+2;
(3) x<4; (4)-5x>20.
感悟新知
知3-练
(1)x-1>2,x-1+1>2+1 (不等式的基本性质 1)
x>3.
(2)2x<x+2, 2x-x<x+2-x (不等式的基本性质 1)
x<2.
(3) x<4
3× x< 3×4 (不等式的基本性质 2)
x<12.
解:
感悟新知
知3-练
(4)-5x>20
(不等式的基本性质 3)
x<-4.
知3-讲
总 结
感悟新知
正确运用不等式的基本性质是解题的关键.
1.
感悟新知
知3-练
已知a<b,请用“>”或“<”填空:
(1) a_____ b;
已知a>b,请用“>”或“<”填空:
(2)-a_____-b;(3) _____ .
>
<
<
2.
感悟新知
知3-练
(1)-10x<-5,
(不等式的基本性质3),
x> .
把下列不等式化为“x>a”或“x<a”的形式:
(1)-10x<-5; (2)-4x<x+5;
(3) +1>x; (4) .
解:
感悟新知
知3-练
(2)-4x<x+5,-4x-x<x+5-x,-5x<5,
-5x÷(-5)>5÷(-5),所以x>-1.
(3) +1>x, +1-x-1>x-x-1,- >-1,
- ×(-2)<-1×(-2),所以x<2.
感悟新知
知3-练
(4)- > ,6× >6× ,
-3(x+1)>2(2x-1),-3x-3>4x-2,
-3x-3-4x+3>4x-2-4x+3,-7x>1,
-7x÷(-7)<1÷(-7),所以x<- .
3.
感悟新知
知3-练
m<0.
已知a>b,则- a+c______(填“>”“<”或
“=”) - b+c.
已知a<b,且ma>mb,求m的取值范围.
<
4.
解:
5.
感悟新知
知3-练
表示1-a和1+a的点在数轴上的位置如图所示,请确定a的取值范围.
由题意,可得1-a<1+a,在不等式的两边都减去1,得-a0.
解:
6.
感悟新知
知3-练
已知数a,b满足a+1>b+1,则下列选项错误的为
( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
7.
感悟新知
知3-练
下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得-2a>-2b
C.由a>b,得-a<-b
D.由a>b,得a-2<b-2
C
8.
感悟新知
知3-练
有理数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c B.a+cC.ac>bc D. <
D
课堂小结
不等式的性质
知识总结 知识方法要点 关键总结 注意事项
不等式的 基本性质1 不等式的两边都加上(或减去)同一个整式,不等号的方向不变. 不变号
不等式的 基本性质2 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 不变号(注意不能为0)
课堂小结
不等式的性质
不等式的基本性质3 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变. 变号
不等式的基本性质4 如果a>b,那么b<a 变号
课堂小结
不等式的性质
方法规律总结:
不等式的基本性质与等式的基本性质的区别和联系.
区别:等式两边都乘(或除以)同一个负数时,等式仍然
成立,不等式的两边都乘(或除以)同一个负数时,不
等号的方向改变;
课堂小结
不等式的性质
联系:无论是等式还是不等式,在它们的两边同时加
(或减)同一个整式及两边同时乘(或除以)同一个正数,
它们仍然成立
10.2 不等式的性质
第十章 一元一次不等式和一元一次不等式组
课时导入
请同学们回顾等式的基本性质:
1. 等式两边同时加上(或减去)同一个代数式,等式仍然
成立.
2. 等式两边同时乘同一个数(或除以同一个不为0的数),
等式仍然成立.
知识回顾
课时导入
利用等式的基本性质可以解方程.类似地,利用不
等式的基本性质 也可以解不等式.那么,不等式具有什
么性质呢?
导入新知
知识点
不等式的基本性质1
知1-讲
感悟新知
1
在数轴上,与a+3,b+3对应的点和与a,b对应的
点之间具有如下的位置关系:
数 点的位置变化
a+3 相当于将与a对应的点向右平移3个单位长度
b+3 相当于将与b对应的点向右平移3个单位长度
知1-讲
感悟新知
(1)确定a+3和b+3的大小.
(2)如果c>0,那么对于a+c和b+c的大小,你有什
么猜想?
(3)在不等式a>b的两边都减去同一个数或同一个整
式,你认为应该有什么结论
知1-讲
总 结
感悟新知
不等式两边都加上(或减去)同一个数或同一个整
式,不等号的方向不变.即
不等式的基本性质 1
如果a>b,那么a±c>b±c.
感悟新知
知1-练
例 1
分析:
从变形来看,是利用了不等式的基本性质1.
(1)根据不等式基本性质1,不等式两边同时减去6;
(2)根据不等式基本性质1,不等式两边同时减去6x.
指出下列不等式是如何变形的,并说明其变形的依据.
(1)若6+y>-7,则y>-13;
(2)若7x<6x+3,则x<3.
解:
知1-讲
总 结
感悟新知
判断某个不等式变形的根据:
一看不等号的方向是不是改变,二看式子的变化情况.
感悟新知
知1-练
1.
已知a<b,请用“>”或“<”填空:
(1)a-2_____b-2; (2) a+c_____b+c.
已知a>b,请用“>”或“<”填空:
(3)a+ _____b+ ;(4)a-6_____b-6.
<
<
>
>
感悟新知
知1-练
2.
把下列不等式化为“x>a”或“x<a”的形式:
(1)x+3<-2; (2)x-5<9.
(1)x+3<-2,
x+3-3<-2-3(不等式的基本性质1),
x<-5.
(2)x-5<9,x-5+5<9+5,所以x<14.
解:
感悟新知
知1-练
3.
已知a<b,用“>”或“<”填空:
(1)a+2________b+2;
(2)a-3________b-3;
(3)a+c________b+c;
(4)a-b________0.
<
<
<
<
感悟新知
知1-练
4.
设“△”“□”表示两种不同的物体,现用天平称,情况如图所示,设“△”的质量为a kg,“□”的质量为b kg,则可得a与b的大小关系是a ________b.
<
感悟新知
知1-练
5.
下列推理正确的是( )
A.因为a<b,所以a+2<b+1
B.因为a<b,所以a-1<b-2
C.因为a>b,所以a+c>b+c
D.因为a>b,所以a+c>b-d
C
感悟新知
知1-练
6.
由a-3<b+1,可得到结论( )
A.a<b
B.a+3<b-1
C.a-1<b+3
D.a+1<b-3
C
不等式的基本性质2
知识点
知2-讲
感悟新知
2
比较大小
由此我们可以得到:不等式的两边都乘以(或除以)
同一个正数,不等号的方向不变.
(-16)__(- 24);
(-16)×4__(- 24)×4;
(-16)÷3__(-24)÷3
8__12;
8×4__12×4;
8÷3__12÷3
知2-讲
总 结
感悟新知
不等式的两边都乘以(或除以)同一个正数,不等号的
方向不变.即
不等式的基本性质 2
如果 a>b,且c>0,那么ac>bc.
感悟新知
知2-练
例2
导引:
已知实数a、b ,若a>b ,则下列结论正确的
是( )
A.a-5<b-5 B.2+a<2+b
C. D.3a>3b
D
不等式的两边同时加上或减去一个数,不等号的方
向不变,不等式的两边同时除以或乘以一个正数,
不等号的方向也不变,所以A、B、C错误,选D.
知2-讲
总 结
感悟新知
在应用不等式的基本性质2时,除了注意“两同”
要求外,还要注意“正数”的要求;另外,乘除运
算可以灵活选择.
感悟新知
知2-练
1.
已知a<b,请用“>”或“<”填空:
(1)3a_____3b;
已知a>b,请用“>”或“<”填空:
(2)4a_____4b;(3) _____ .
<
>
>
2.
感悟新知
知2-练
解:
把下列不等式化为“x>a”或“x<a”的形式:
(1)9x>8x+1; (2) x>-4;
(3)6x<4x-2; (4) x>x+4.
(1)9x>8x+1,
9x-8x>8x+1-8x(不等式的基本性质1),x>1.
(2) x>-4,
2× x>2×(-4)(不等式的基本性质2),x>-8.
感悟新知
知2-练
(3)6x<4x-2,6x-4x<4x-2-4x,2x<-2,
2x÷2<(-2)÷2,所以x<-1.
(4) x>x+4, x-x>x+4-x, x>4,
x× >4× ,所以x>6.
3.
感悟新知
知2-练
若x>y,则4x-3________4y-3.(填“>”“<”或“=”)
由3a<4b,两边____________________,可变形为
a< b.
>
同乘 (或同除以12)
4.
5.
感悟新知
知2-练
m>n,则下列不等式不一定成立的是( )
A.m+2>n+2 B.2m>2n
C. > D.m2<n2
D
6.
感悟新知
知2-练
若3x>-3y,则下列不等式中一定成立的是( )
A.x+y>0 B.x-y>0
C.x+y<0 D.x-y<0
A
7.
感悟新知
知2-练
当0<x<1时,x2,x, 的大小顺序是( )
A.x2
不等式的基本性质3
知识点
知3-讲
感悟新知
3
1. 如果a>b,那么它们的相反数-a与-b哪个大,
你能用数轴上点的位置关系和具体的例子加以说
明吗?
2. 如果a>b ,那么-a<-b,这个式子可理解为:
a×(-1)<b×(-1)
这样,对于不等式a>b,两边同乘以-3,会
得到什么结果呢?
知3-讲
感悟新知
a>b a×(-1)<b×(-1) a×(-3)<b×(-3).
×(-1)
×3
×(-3)
3. 如果a>b,c<0,那么ac与bc有怎样的大小关系?
知3-讲
总 结
感悟新知
不等式两边都乘(或除以)同一个负数,不等号的方向
改变.即
不等式的基本性质 3
如果 a>b,且c<0,那么ac<bc.
知3-讲
感悟新知
特别解读
1. 不等式的三条基本性质是不等式变形的依据,运用
不等式的基本性质时,不等式的两边要同时进行相同的变形 .
2. 在不等式的变形中,还常用到性质:
(1)对称性:若 a>b, 则 b
感悟新知
知3-练
例 3
根据不等式的基本性质,把下列不等式化为“x>a”或“x<a”的形式:
(1)x-1>2; (2)2x<x+2;
(3) x<4; (4)-5x>20.
感悟新知
知3-练
(1)x-1>2,x-1+1>2+1 (不等式的基本性质 1)
x>3.
(2)2x<x+2, 2x-x<x+2-x (不等式的基本性质 1)
x<2.
(3) x<4
3× x< 3×4 (不等式的基本性质 2)
x<12.
解:
感悟新知
知3-练
(4)-5x>20
(不等式的基本性质 3)
x<-4.
知3-讲
总 结
感悟新知
正确运用不等式的基本性质是解题的关键.
1.
感悟新知
知3-练
已知a<b,请用“>”或“<”填空:
(1) a_____ b;
已知a>b,请用“>”或“<”填空:
(2)-a_____-b;(3) _____ .
>
<
<
2.
感悟新知
知3-练
(1)-10x<-5,
(不等式的基本性质3),
x> .
把下列不等式化为“x>a”或“x<a”的形式:
(1)-10x<-5; (2)-4x<x+5;
(3) +1>x; (4) .
解:
感悟新知
知3-练
(2)-4x<x+5,-4x-x<x+5-x,-5x<5,
-5x÷(-5)>5÷(-5),所以x>-1.
(3) +1>x, +1-x-1>x-x-1,- >-1,
- ×(-2)<-1×(-2),所以x<2.
感悟新知
知3-练
(4)- > ,6× >6× ,
-3(x+1)>2(2x-1),-3x-3>4x-2,
-3x-3-4x+3>4x-2-4x+3,-7x>1,
-7x÷(-7)<1÷(-7),所以x<- .
3.
感悟新知
知3-练
m<0.
已知a>b,则- a+c______(填“>”“<”或
“=”) - b+c.
已知a<b,且ma>mb,求m的取值范围.
<
4.
解:
5.
感悟新知
知3-练
表示1-a和1+a的点在数轴上的位置如图所示,请确定a的取值范围.
由题意,可得1-a<1+a,在不等式的两边都减去1,得-a
解:
6.
感悟新知
知3-练
已知数a,b满足a+1>b+1,则下列选项错误的为
( )
A.a>b B.a+2>b+2
C.-a<-b D.2a>3b
D
7.
感悟新知
知3-练
下列不等式变形正确的是( )
A.由a>b,得ac>bc
B.由a>b,得-2a>-2b
C.由a>b,得-a<-b
D.由a>b,得a-2<b-2
C
8.
感悟新知
知3-练
有理数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
A.a-c>b-c B.a+c
D
课堂小结
不等式的性质
知识总结 知识方法要点 关键总结 注意事项
不等式的 基本性质1 不等式的两边都加上(或减去)同一个整式,不等号的方向不变. 不变号
不等式的 基本性质2 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 不变号(注意不能为0)
课堂小结
不等式的性质
不等式的基本性质3 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变. 变号
不等式的基本性质4 如果a>b,那么b<a 变号
课堂小结
不等式的性质
方法规律总结:
不等式的基本性质与等式的基本性质的区别和联系.
区别:等式两边都乘(或除以)同一个负数时,等式仍然
成立,不等式的两边都乘(或除以)同一个负数时,不
等号的方向改变;
课堂小结
不等式的性质
联系:无论是等式还是不等式,在它们的两边同时加
(或减)同一个整式及两边同时乘(或除以)同一个正数,
它们仍然成立
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
