复龙初中八年级上册第13章整式的乘除综合测试及答案
文档属性
| 名称 | 复龙初中八年级上册第13章整式的乘除综合测试及答案 | 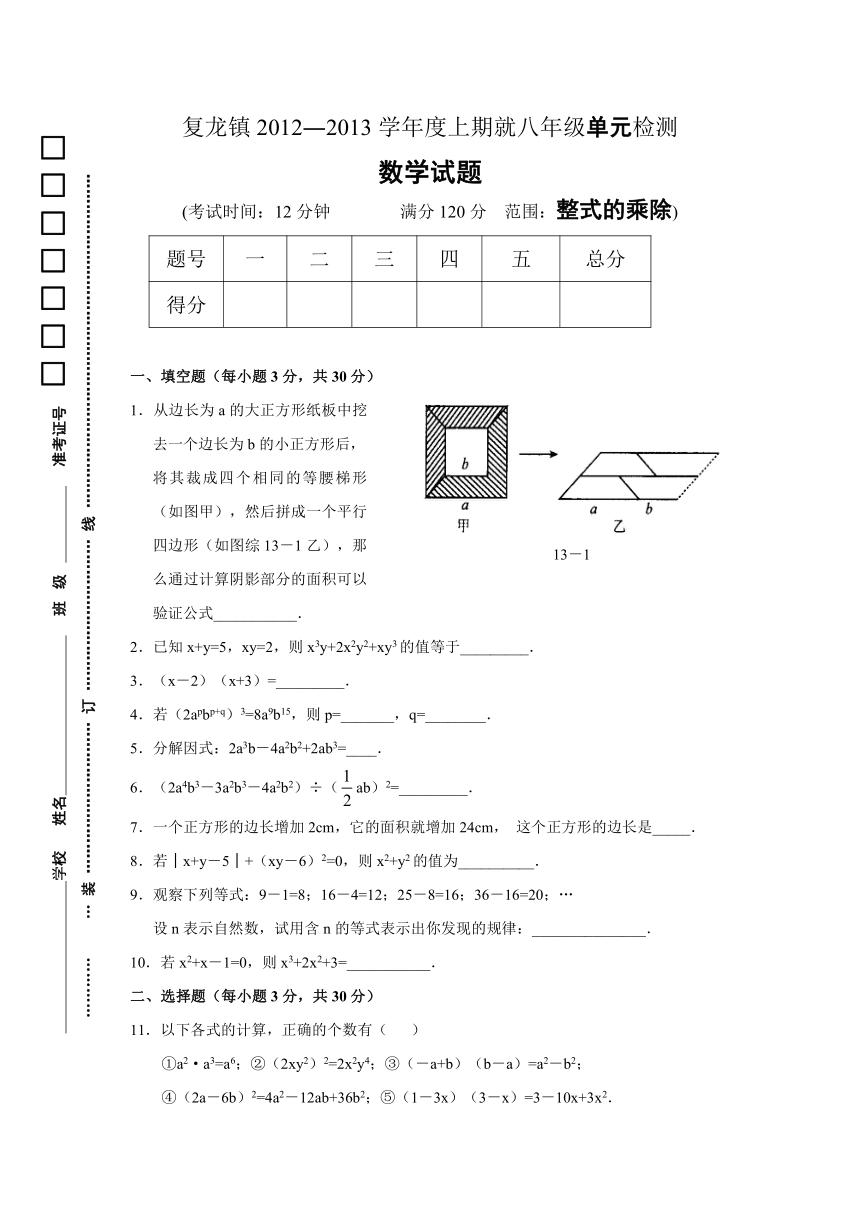 | |
| 格式 | zip | ||
| 文件大小 | 30.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 13:51:05 | ||
图片预览



文档简介
复龙镇2012―2013学年度上期就八年级单元检测
数学试题
(考试时间:12分钟 满分120分 范围:整式的乘除)
题号
一
二
三
四
五
总分
得分
一、填空题(每小题3分,共30分)
1.从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图综13-1乙),那么通过计算阴影部分的面积可以验证公式___________.
2.已知x+y=5,xy=2,则x3y+2x2y2+xy3的值等于_________.
3.(x-2)(x+3)=_________.
4.若(2apbp+q)3=8a9b15,则p=_______,q=________.
5.分解因式:2a3b-4a2b2+2ab3=____.
6.(2a4b3-3a2b3-4a2b2)÷(ab)2=_________.
7.一个正方形的边长增加2cm,它的面积就增加24cm,这个正方形的边长是_____.
8.若│x+y-5│+(xy-6)2=0,则x2+y2的值为__________.
9.观察下列等式:9-1=8;16-4=12;25-8=16;36-16=20;…
设n表示自然数,试用含n的等式表示出你发现的规律:_______________.
10.若x2+x-1=0,则x3+2x2+3=___________.
二、选择题(每小题3分,共30分)
11.以下各式的计算,正确的个数有( )
①a2·a3=a6;②(2xy2)2=2x2y4;③(-a+b)(b-a)=a2-b2;
④(2a-6b)2=4a2-12ab+36b2;⑤(1-3x)(3-x)=3-10x+3x2.
A.0个 B.1个 C.2个 D.3个
12.下列因式分解中,错误的是( )
A.1-9x2=(1+3x)(1-3x) B.a2-a+=(a-)2
C.-mx+my=-m(x+y) D.ax-ay-bx+by=(a-b)(x-y)
13.使(-am)n=-amn(a≠0)成立,指数n可取( )
A.正数 B.正奇数 C.正偶数 D.自然数
14.若a的值使得x2+4x+a=(x+2)2-1成立,则a的值为( )
A.5 B.4 C.3 D.2
15.若(8×106)(5×102)(2×10)=M×10a,则M、a的值为( )
A.M=8,a=8 B.M=2,a=9 C.M=8,a=10 D.M=5,a=10
16.若x,y是正整数,且2x·2y=25,则x,y的值有( )
A.4对 B.3对 C.2对 D.1对
17.如果(x2+px+q)(x2-3x+2)的展开式中不含x2项和x项,则p,q的值分别为( )
A.p=0,q=0 B.p=-3,q=-9 C.p=,q= D.p=-3,q=1
18.已知(a-b)2=7,(a+b)2=13,则a2+b2与ab的值分别是( )
A.10, B.10,3 C.20, D.20,3
19.已知(x+y+z)2=25,xy+yz+xz=7,那么x2+y2+z2=( )
A.-9 B.-11 C.11 D.18
20.若a2+2a+b2-6b+10=0,则( )
A.a=1,b=3 B.a=-1,b=-3 C.a=1,b=-3 D.a=-1,b=3
三、解答题(共60分)
21.计算(每题3分,共12分)
(1)(6x-4)(3x+2); (2)(3x-2y)2-(3x-y)(3x+y);
(3)(10x4-15x2-5x)÷(-5x); (4)20022-2001×2003-9992.
22.分解因式(每题4分,共8分)
(1)30x2n+1-25x2n+5xn; (2)x2-4y2+x-2y.
23.(4分)如图综13-2,请用两种不同的方式表示大正方形的面积.
根据上述结果可以验证哪个乘法公式?
24.(6分)已知2a=3,4b=5,8c=7,求8a+c-2b的值.
25.(6分)分解因式x2+ax+b,甲看错了a的值,分解的结果是(x+6)(x-1),乙看错了b的值,分解的结果是(x-2)·(x+1),那么x2+ax+b分解因式的正确结果为多少?
26.(8分)已知A=3x+2,B=2-3x,C=4x-5.
(1)求A·B-B·C-B2;(2)当x=-时,求上式的值.
27.(8分)一条水渠,其横断面为梯形,如图综13-3,根据图中的长度求出横断面面积的代数式,并计算当a=2,b=0.8时的面积.
28.(8分)已知△ABC三边长分别为a、b、c,且a、b、c满足等式
3(a2+b2+c2)=(a+b+c)2,试判断△ABC的形状.
答案:
1.a2-b2=(a+b)(a-b)
2.50(点拨:原式=xy(x2+2xy+y2)=xy(x+y)2,再代入即可)
3.x2+x-6 4a2-25b2 4.3 2 5.2ab(a-b)2
6.8a2b-12b-16
7.5(点拨:设这个正方形的边长为a,依题意有(a+2)2-a2=24,
所以4a+4=24,所以a=5)
8.13(点拨:由│x+y-5│+(xy-6)2=0知,x+y=5,xy=6,所以(x+y)2=25,即x2+y2+2xy=25,所以x2+y2=25-2×6=13)
9.(n+2)2-n2=4n+4(n≥1的自然数)
10.4(点拨:由x2+x-1=0得x2+x=1,
所以x3+2x2+3=x3+x2+x2+3=x(x2+x)+x2+3=x+x2+3=1+3=4)
11.B 12.C 13.B 14.C 15.C 16.A
17.C(点拨:(x2+px+q)(x2-3x+2)的展开式为
x4+(p-3)x3+(2-3p+q)x2+(2p-3q)x+2q,
因其展开式中不含x2项和x项,
故2-3p+q=0,且2p-3q=0,
所以p=,q=)
18.A(点拨:因为(a-b)2=7,(a+b)2=13,
所以a2+b2-2ab=7①,a2+b2+2ab=13②,
所以①+②得a2+b2=10,①-②得ab=,选A)
19.C
20.D(点拨:因为a2+2a+b2-6b+10=0,所以(a2+2a+1)+(b2-6b+9)=0,
所以(a+1)2+(b-3)2=0,所以a=-1,b=3,故选D)
21.(1)原式=18x2+12x-12x-8=18x2-8;
(2)原式=9x2-12xy+4y2-9x2+y2=5y2-12xy;
(3)原式=-2x3+3x+1;
(4)原式=20022-(2002-1)(2002+1)-9992
=20022-20022+1-9992
=1-9992=(1+999)(1-999)
=-998000.
22.(1)原式=5xn(6xn+1-5xn+1);
(2)原式=(x-2y)(x+2y+1).
23.(a+b)2=a2+b2+2ab.
24.8a+c-2b=23a+3c-6b=.
25.因为甲看错了a的值,分解的结果为(x+6)(x-1),
所以b=-6,又因为乙看错了b的值,分解的结果是(x-2)(x+1),所以a=-1.
所以x2+ax+b=x2-x-6=(x+2)(x-3).
26.(1)因为A=3x+2,B=2-3x,C=4x-5.
所以A·B-B·C-B2
=(3x+2)(2-3x)-(2-3x)(4x-5)-(2-3x)2
=4-9x2-8x+10+12x2-15x-4+12x-9x2
=-6x2-11x+10;
(2)当x=-时,
原式=-6x2-11x+10=-6×+11×+10=14.
27.S=a2-b2,当a=2,b=0.8时,S=3.36.
解:∵ 3(a2+b2+c2)=(a+b+c)2
展开后可变为:2(a2+b2+c2)=2(ab+bc+ac),
即2(a2+b2+c2)-2(ab+bc+ac)=0,
所以该式进一步可变为:(a-b)2+(b-c)2+(a-c)2=0,
数学试题
(考试时间:12分钟 满分120分 范围:整式的乘除)
题号
一
二
三
四
五
总分
得分
一、填空题(每小题3分,共30分)
1.从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图综13-1乙),那么通过计算阴影部分的面积可以验证公式___________.
2.已知x+y=5,xy=2,则x3y+2x2y2+xy3的值等于_________.
3.(x-2)(x+3)=_________.
4.若(2apbp+q)3=8a9b15,则p=_______,q=________.
5.分解因式:2a3b-4a2b2+2ab3=____.
6.(2a4b3-3a2b3-4a2b2)÷(ab)2=_________.
7.一个正方形的边长增加2cm,它的面积就增加24cm,这个正方形的边长是_____.
8.若│x+y-5│+(xy-6)2=0,则x2+y2的值为__________.
9.观察下列等式:9-1=8;16-4=12;25-8=16;36-16=20;…
设n表示自然数,试用含n的等式表示出你发现的规律:_______________.
10.若x2+x-1=0,则x3+2x2+3=___________.
二、选择题(每小题3分,共30分)
11.以下各式的计算,正确的个数有( )
①a2·a3=a6;②(2xy2)2=2x2y4;③(-a+b)(b-a)=a2-b2;
④(2a-6b)2=4a2-12ab+36b2;⑤(1-3x)(3-x)=3-10x+3x2.
A.0个 B.1个 C.2个 D.3个
12.下列因式分解中,错误的是( )
A.1-9x2=(1+3x)(1-3x) B.a2-a+=(a-)2
C.-mx+my=-m(x+y) D.ax-ay-bx+by=(a-b)(x-y)
13.使(-am)n=-amn(a≠0)成立,指数n可取( )
A.正数 B.正奇数 C.正偶数 D.自然数
14.若a的值使得x2+4x+a=(x+2)2-1成立,则a的值为( )
A.5 B.4 C.3 D.2
15.若(8×106)(5×102)(2×10)=M×10a,则M、a的值为( )
A.M=8,a=8 B.M=2,a=9 C.M=8,a=10 D.M=5,a=10
16.若x,y是正整数,且2x·2y=25,则x,y的值有( )
A.4对 B.3对 C.2对 D.1对
17.如果(x2+px+q)(x2-3x+2)的展开式中不含x2项和x项,则p,q的值分别为( )
A.p=0,q=0 B.p=-3,q=-9 C.p=,q= D.p=-3,q=1
18.已知(a-b)2=7,(a+b)2=13,则a2+b2与ab的值分别是( )
A.10, B.10,3 C.20, D.20,3
19.已知(x+y+z)2=25,xy+yz+xz=7,那么x2+y2+z2=( )
A.-9 B.-11 C.11 D.18
20.若a2+2a+b2-6b+10=0,则( )
A.a=1,b=3 B.a=-1,b=-3 C.a=1,b=-3 D.a=-1,b=3
三、解答题(共60分)
21.计算(每题3分,共12分)
(1)(6x-4)(3x+2); (2)(3x-2y)2-(3x-y)(3x+y);
(3)(10x4-15x2-5x)÷(-5x); (4)20022-2001×2003-9992.
22.分解因式(每题4分,共8分)
(1)30x2n+1-25x2n+5xn; (2)x2-4y2+x-2y.
23.(4分)如图综13-2,请用两种不同的方式表示大正方形的面积.
根据上述结果可以验证哪个乘法公式?
24.(6分)已知2a=3,4b=5,8c=7,求8a+c-2b的值.
25.(6分)分解因式x2+ax+b,甲看错了a的值,分解的结果是(x+6)(x-1),乙看错了b的值,分解的结果是(x-2)·(x+1),那么x2+ax+b分解因式的正确结果为多少?
26.(8分)已知A=3x+2,B=2-3x,C=4x-5.
(1)求A·B-B·C-B2;(2)当x=-时,求上式的值.
27.(8分)一条水渠,其横断面为梯形,如图综13-3,根据图中的长度求出横断面面积的代数式,并计算当a=2,b=0.8时的面积.
28.(8分)已知△ABC三边长分别为a、b、c,且a、b、c满足等式
3(a2+b2+c2)=(a+b+c)2,试判断△ABC的形状.
答案:
1.a2-b2=(a+b)(a-b)
2.50(点拨:原式=xy(x2+2xy+y2)=xy(x+y)2,再代入即可)
3.x2+x-6 4a2-25b2 4.3 2 5.2ab(a-b)2
6.8a2b-12b-16
7.5(点拨:设这个正方形的边长为a,依题意有(a+2)2-a2=24,
所以4a+4=24,所以a=5)
8.13(点拨:由│x+y-5│+(xy-6)2=0知,x+y=5,xy=6,所以(x+y)2=25,即x2+y2+2xy=25,所以x2+y2=25-2×6=13)
9.(n+2)2-n2=4n+4(n≥1的自然数)
10.4(点拨:由x2+x-1=0得x2+x=1,
所以x3+2x2+3=x3+x2+x2+3=x(x2+x)+x2+3=x+x2+3=1+3=4)
11.B 12.C 13.B 14.C 15.C 16.A
17.C(点拨:(x2+px+q)(x2-3x+2)的展开式为
x4+(p-3)x3+(2-3p+q)x2+(2p-3q)x+2q,
因其展开式中不含x2项和x项,
故2-3p+q=0,且2p-3q=0,
所以p=,q=)
18.A(点拨:因为(a-b)2=7,(a+b)2=13,
所以a2+b2-2ab=7①,a2+b2+2ab=13②,
所以①+②得a2+b2=10,①-②得ab=,选A)
19.C
20.D(点拨:因为a2+2a+b2-6b+10=0,所以(a2+2a+1)+(b2-6b+9)=0,
所以(a+1)2+(b-3)2=0,所以a=-1,b=3,故选D)
21.(1)原式=18x2+12x-12x-8=18x2-8;
(2)原式=9x2-12xy+4y2-9x2+y2=5y2-12xy;
(3)原式=-2x3+3x+1;
(4)原式=20022-(2002-1)(2002+1)-9992
=20022-20022+1-9992
=1-9992=(1+999)(1-999)
=-998000.
22.(1)原式=5xn(6xn+1-5xn+1);
(2)原式=(x-2y)(x+2y+1).
23.(a+b)2=a2+b2+2ab.
24.8a+c-2b=23a+3c-6b=.
25.因为甲看错了a的值,分解的结果为(x+6)(x-1),
所以b=-6,又因为乙看错了b的值,分解的结果是(x-2)(x+1),所以a=-1.
所以x2+ax+b=x2-x-6=(x+2)(x-3).
26.(1)因为A=3x+2,B=2-3x,C=4x-5.
所以A·B-B·C-B2
=(3x+2)(2-3x)-(2-3x)(4x-5)-(2-3x)2
=4-9x2-8x+10+12x2-15x-4+12x-9x2
=-6x2-11x+10;
(2)当x=-时,
原式=-6x2-11x+10=-6×+11×+10=14.
27.S=a2-b2,当a=2,b=0.8时,S=3.36.
解:∵ 3(a2+b2+c2)=(a+b+c)2
展开后可变为:2(a2+b2+c2)=2(ab+bc+ac),
即2(a2+b2+c2)-2(ab+bc+ac)=0,
所以该式进一步可变为:(a-b)2+(b-c)2+(a-c)2=0,
