2021-2022学年安徽省亳州市涡阳县八年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2021-2022学年安徽省亳州市涡阳县八年级(上)期末数学试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 20:20:53 | ||
图片预览



文档简介
2021-2022学年安徽省亳州市涡阳县八年级(上)期末数学试卷
一、单选题(共30分)
1.(3分)在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下面四个交通标志图中为轴对称图形的是
A. B. C. D.
3.(3分)点A(﹣5,y1)和B(﹣2,y2)都在直线上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
4.(3分)若三条线段中,,为奇数,那么由、、为边组成的三角形共有
A.1个 B.3个 C.无数多个 D.无法确定
5.(3分)如图,兔子的三个洞口、、构成,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在
A.三个角的角平分线的交点 B.三条边的垂直平分线的交点
C.三角形三条高的交点 D.三角形三条中线的交点
6.(3分)如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
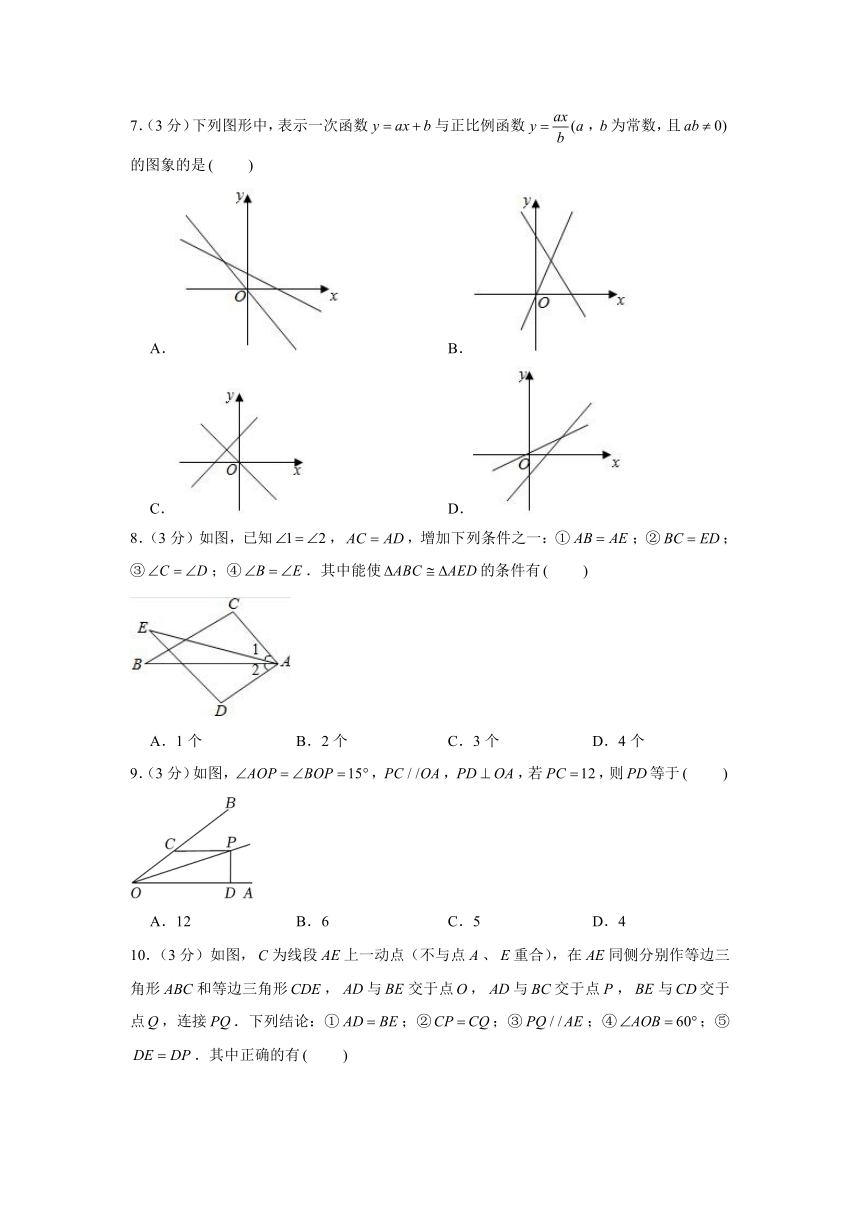
7.(3分)下列图形中,表示一次函数与正比例函数,为常数,且的图象的是
A. B.
C. D.
8.(3分)如图,已知,,增加下列条件之一:①;②;③;④.其中能使的条件有
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,,,,若,则等于
A.12 B.6 C.5 D.4
10.(3分)如图,为线段上一动点(不与点、重合),在同侧分别作等边三角形和等边三角形,与交于点,与交于点,与交于点,连接.下列结论:①;②;③;④;⑤.其中正确的有
A.5个 B.4个 C.3个 D.2个
二、填空题(共16分)
11.(4分)在函数中,自变量的取值范围是 .
12.(4分)命题:“如果,那么”的逆命题是 命题(填“真”或“假” .
13.(4分)如图,的周长为26,的垂直平分线交于点,垂足为,若,则的周长是 .
14.(4分)等腰三角形有一内角的度数为,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为 .
三、解答题(共74分)
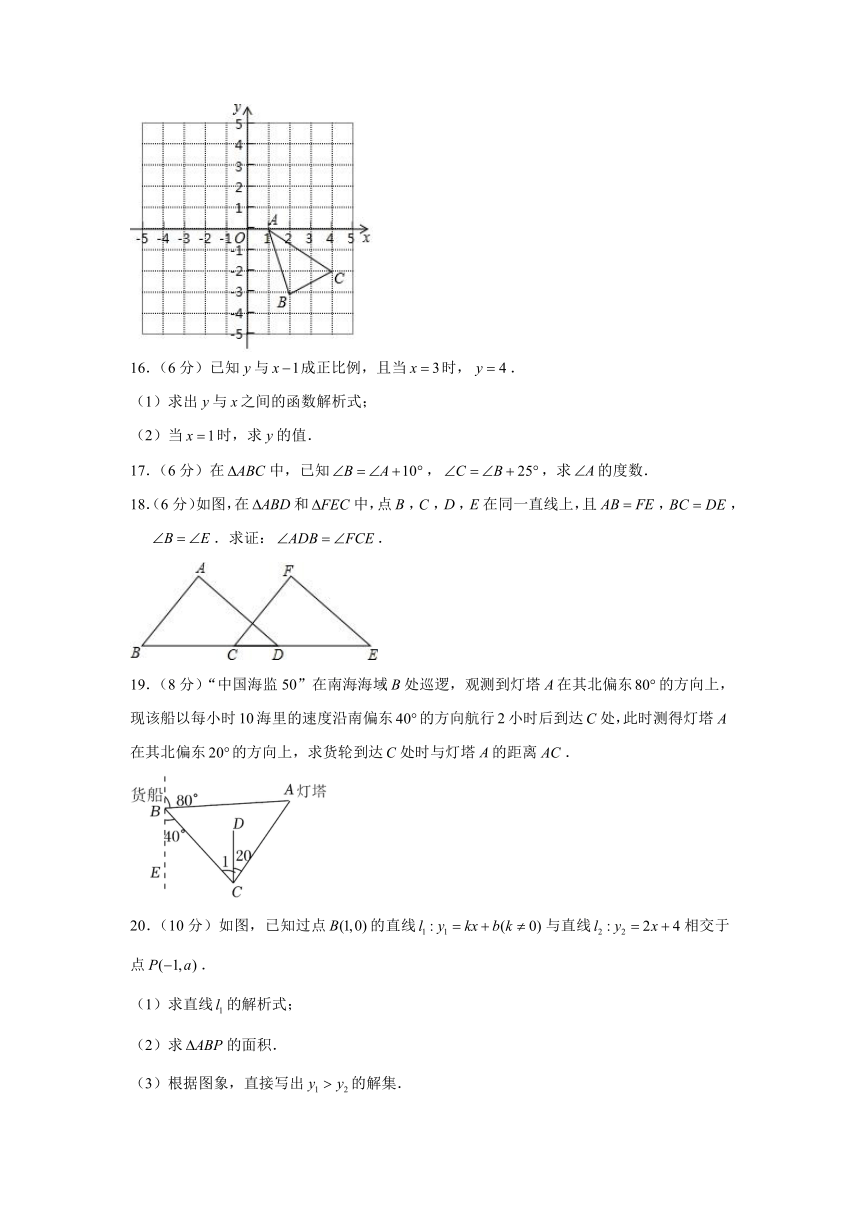
15.(6分)如图,平面直角坐标系中,已知的三个顶点的坐标分别为,,.
(1)画出关于轴的对称图形△;
(2)画出△向左平移4个单位长度后得到的△;
(3)如果上有一点经过上述两次变换,那么对应上的点的坐标是 .
16.(6分)已知与成正比例,且当时,.
(1)求出与之间的函数解析式;
(2)当时,求的值.
17.(6分)在中,已知,,求的度数.
18.(6分)如图,在和中,点,,,在同一直线上,且,,.求证:.
19.(8分)“中国海监50”在南海海域处巡逻,观测到灯塔在其北偏东的方向上,现该船以每小时10海里的速度沿南偏东的方向航行2小时后到达处,此时测得灯塔在其北偏东的方向上,求货轮到达处时与灯塔的距离.
20.(10分)如图,已知过点的直线与直线相交于点.
(1)求直线的解析式;
(2)求的面积.
(3)根据图象,直接写出的解集.
21.(10分)如图,在中,,点、、分别在、、边上,且,.
(1)求证:是等腰三角形;
(2)当时,求的度数.
22.(10分)某商店销售型和型两种型号的电脑,销售一台型电脑可获利120元,销售一台型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的3倍.设购进型电脑台,这100台电脑的销售总利润为元.
(1)求与的函数关系式,并求出自变量的取值范围;
(2)该商店购进型、型电脑各多少台,才能使销售利润最大?最大利润是多少?
23.(12分)如图,把一块直角三角尺的直角顶点放置在水平直线上,在中,,,试回答下列问题:
(1)若把三角尺绕着点按顺时针方向旋转,当时, 度;
(2)在三角尺绕着点按顺时针方向旋转过程中,分别作于,与,若,,求.
(3)三角尺绕着点按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.
参考答案与解析
一、单选题(共30分)
1.(3分)在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据各象限内点的坐标特征解答.
【解答】解:点在第四象限.
故选:.
2.(3分)下面四个交通标志图中为轴对称图形的是
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:、不是轴对称图形,故本选项不符合题意;
、是轴对称图形,故本选项符合题意;
、不是轴对称图形,故本选项不符合题意;
、不是轴对称图形,故本选项不符合题意.
故选:.
3.(3分)点A(﹣5,y1)和B(﹣2,y2)都在直线上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
【分析】由k=>0,利用一次函数的性质可得出y随x的增大而增大,结合﹣5<﹣2,即可得出y1<y2.
【解答】解:∵k=>0,
∴y随x的增大而增大,
又∵点A(﹣5,y1)和B(﹣2,y2)都在直线上,且﹣5<﹣2,
∴y1<y2.
故选:C.
4.(3分)若三条线段中,,为奇数,那么由、、为边组成的三角形共有
A.1个 B.3个 C.无数多个 D.无法确定
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,求得第三边的取值范围,再进一步根据是奇数进行分析求解.
【解答】解:根据三角形的三边关系,得
,.
又是奇数,则或5或7.
故选:.
5.(3分)如图,兔子的三个洞口、、构成,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在
A.三个角的角平分线的交点 B.三条边的垂直平分线的交点
C.三角形三条高的交点 D.三角形三条中线的交点
【分析】用线段垂直平分线性质判断即可.
【解答】解:猎狗到三个顶点的距离相等,则猎狗应蹲守在的三条边垂直平分线的交点.
故选:.
6.(3分)如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
【分析】根据三角形中线的性质,先求得的面积,再求得的面积,即可求得的面积.
【解答】解:,为的中点,
,
为的中点,
,
为的中点,
,
故选:.
7.(3分)下列图形中,表示一次函数与正比例函数,为常数,且的图象的是
A. B.
C. D.
【分析】将、与0进行比较,然后分情况讨论其图象的位置.
【解答】解:若,,
则函数图象经过一、二、三象限,函数图象经过一、三象限,
若,,
则函数图象经经过一、三、四象限,函数图象经过二、四象限,
若,
则函数图象经经过二、三、四象限,函数图象经过一、三象限,
若,
则函数图象经经过一、二、四象限,函数图象经过二、四象限,
故选:.
8.(3分)如图,已知,,增加下列条件之一:①;②;③;④.其中能使的条件有
A.1个 B.2个 C.3个 D.4个
【分析】先由得到,然后分别利用“”、“ ”和“”对各添加的条件进行判断.
【解答】解:,
,
,
当时,可根据“”判断;
当时,不能判断;
当时,可根据“”判断;
当时,可根据“”判断.
故选:.
9.(3分)如图,,,,若,则等于
A.12 B.6 C.5 D.4
【分析】过点作于,如图,根据角平分线的性质得到,再利用平行线的性质得到,接着根据含30度的直角三角形三边的关系得到,从而得到的长.
【解答】解:过点作于,如图,
,
平分,,
而,,
,
,
,
,
.
故选:.
10.(3分)如图,为线段上一动点(不与点、重合),在同侧分别作等边三角形和等边三角形,与交于点,与交于点,与交于点,连接.下列结论:①;②;③;④;⑤.其中正确的有
A.5个 B.4个 C.3个 D.2个
【分析】首先利用证明,得,,可说明①④正确;再利用说明,得,由,得是等边三角形,可说明②③正确,由,得,故⑤错误.
【解答】解:、是等边三角形,
,,,
,
,
,,
,
,
故①④正确;
,,,
,
,
,
是等边三角形,
,
,
故②③正确,
,
,
故⑤错误,
正确的有4个,
故选:.
二、填空题(共16分)
11.(4分)在函数中,自变量的取值范围是 且 .
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
【解答】解:根据二次根式有意义,分式有意义得:且,
解得:且.
故答案为且.
12.(4分)命题:“如果,那么”的逆命题是 假 命题(填“真”或“假” .
【分析】直接利用逆命题的写法就是将原命题的结论与题设交换进而得出答案.
【解答】解:命题:“如果,那么”的逆命题是如果,那么,是假命题;
故答案为:假.
13.(4分)如图,的周长为26,的垂直平分线交于点,垂足为,若,则的周长是 16 .
【分析】根据线段垂直平分线的性质得到,,根据三角形的周长公式计算即可.
【解答】解:是的垂直平分线,,
,,
的周长为26,
,
,
的周长,
故答案为:16.
14.(4分)等腰三角形有一内角的度数为,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为 或 .
【分析】根据题意,一种情况为顶角是,根据直角三角形两锐角互余即可推出所求角为,另一种情况为底角是,根据等腰三角形以及三角形内角和定理推出顶角是,再根据直角三角形两锐角互余即可推出所求角为.
【解答】解:①此等腰三角形顶角是,如图1.
在中,,,
;
②此等腰三角形底角是,如图2,
,,
,
.
,
在中,,,
.
综上可知,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为或.
故答案为:或.
三、解答题(共74分)
15.(6分)如图,平面直角坐标系中,已知的三个顶点的坐标分别为,,.
(1)画出关于轴的对称图形△;
(2)画出△向左平移4个单位长度后得到的△;
(3)如果上有一点经过上述两次变换,那么对应上的点的坐标是 .
【分析】(1)利用轴对称的性质即可画图;
(2)利用平移的性质即可画图;
(3)根据平面直角坐标系中点的变化规律可得出答案.
【解答】解:(1)如图,△即为所求;
(2)如图,△即为所求;
(3)点经过上述两次变换,那么对应上的点的坐标为,
故答案为:.
16.(6分)已知与成正比例,且当时,.
(1)求出与之间的函数解析式;
(2)当时,求的值.
【分析】(1)利用正比例函数的定义,设,然后把已知的一组对应值代入求出即可得到与的关系式;
(2)利用(1)中关系式求出自变量为1时对应的函数值即可.
【解答】解:(1)设,
把,代入得,解得,
所以,
即;
(2)当时,.
17.(6分)在中,已知,,求的度数.
【分析】将第一个等式代入第二等式用表示出,再根据三角形的内角和等于列方程求出,然后求解即可.
【解答】解:,,
,
由三角形内角和定理得,,
所以,,
解得.
18.(6分)如图,在和中,点,,,在同一直线上,且,,.求证:.
【分析】根据等式的性质得出,再利用得出:与全等,进而得出.
【解答】证明:,
,
即,
在与中,
,
,
.
19.(8分)“中国海监50”在南海海域处巡逻,观测到灯塔在其北偏东的方向上,现该船以每小时10海里的速度沿南偏东的方向航行2小时后到达处,此时测得灯塔在其北偏东的方向上,求货轮到达处时与灯塔的距离.
【分析】利用平行线性质得出:,,进而得出,得出是等边三角形,进而得出答案.
【解答】解:由题意得:,(海里),
,
,
,
,
是等边三角形,
海里,
答:货轮到达处时与灯塔的距离为20海里.
20.(10分)如图,已知过点的直线与直线相交于点.
(1)求直线的解析式;
(2)求的面积.
(3)根据图象,直接写出的解集.
【分析】(1)由点在直线上,利用一次函数图象上点的坐标特征,即可求出值,再利用点的坐标和点的坐标可求直线的解析式;
(2)由解析式求得、的坐标,即可求得,然后根据三角形面积公式即可求得;
(3)不等式即的函数值大于的函数值,观察函数图象得到当时满足条件;
【解答】解:(1)点在直线上,
,即,
则的坐标为,
由题意,得,解得:.
的解析式为:;
(2)直线与轴相交于点,
点的坐标为,则,
.
(3)由图象可知,不等式的解集是.
21.(10分)如图,在中,,点、、分别在、、边上,且,.
(1)求证:是等腰三角形;
(2)当时,求的度数.
【分析】(1)根据等边对等角可得,利用“边角边”证明和全等,根据全等三角形对应边相等可得,再根据等腰三角形的定义证明即可;
(2)根据全等三角形对应角相等可得,然后求出,再利用三角形的内角和定理和平角的定义求出.
【解答】(1)证明:,
,
在和中,
,
,
,
是等腰三角形;
(2)解:,
,
,
,
,
,
,,
,
.
22.(10分)某商店销售型和型两种型号的电脑,销售一台型电脑可获利120元,销售一台型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的3倍.设购进型电脑台,这100台电脑的销售总利润为元.
(1)求与的函数关系式,并求出自变量的取值范围;
(2)该商店购进型、型电脑各多少台,才能使销售利润最大?最大利润是多少?
【分析】(1)用型电脑、型电脑的利润相加,即得与的函数关系式,根据型电脑的进货量不超过型电脑的3倍可得,即可得自变量的取值范围;
(2)根据一次函数的性质即可得答案.
【解答】解:(1)由题意可得,型电脑的总利润为:,型电脑的总利润为:,
、电脑的总利润:,
与的函数关系式为:,
又型电脑的进货量不超过型电脑的3倍,
,
解得:,
自变量的取值范围为:,且为正整数,
,且为正整数);
(2),且,
随的增大而减小,
,且为正整数,
时,有最大值为:,
型电脑进货25台,型电脑进货75台,销售利润最大为13500元.
23.(12分)如图,把一块直角三角尺的直角顶点放置在水平直线上,在中,,,试回答下列问题:
(1)若把三角尺绕着点按顺时针方向旋转,当时, 45 度;
(2)在三角尺绕着点按顺时针方向旋转过程中,分别作于,与,若,,求.
(3)三角尺绕着点按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.
【分析】(1)先求出,再用平行线的性质,即可求出答案;
(2)先用同角的余角相等判断出,同理:,进而判断出,得出,,即可求出答案;
(3)同(2)的方法,即可得出结论.
【解答】解:(1)在中,,,
,
,
,
故答案为45;
(2)于,于,
,.
,
又,
,
同理:,
在和中,
,
,
,,
;
(3),理由:
同(2)的方法得,,
,,
.
一、单选题(共30分)
1.(3分)在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下面四个交通标志图中为轴对称图形的是
A. B. C. D.
3.(3分)点A(﹣5,y1)和B(﹣2,y2)都在直线上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
4.(3分)若三条线段中,,为奇数,那么由、、为边组成的三角形共有
A.1个 B.3个 C.无数多个 D.无法确定
5.(3分)如图,兔子的三个洞口、、构成,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在
A.三个角的角平分线的交点 B.三条边的垂直平分线的交点
C.三角形三条高的交点 D.三角形三条中线的交点
6.(3分)如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
7.(3分)下列图形中,表示一次函数与正比例函数,为常数,且的图象的是
A. B.
C. D.
8.(3分)如图,已知,,增加下列条件之一:①;②;③;④.其中能使的条件有
A.1个 B.2个 C.3个 D.4个
9.(3分)如图,,,,若,则等于
A.12 B.6 C.5 D.4
10.(3分)如图,为线段上一动点(不与点、重合),在同侧分别作等边三角形和等边三角形,与交于点,与交于点,与交于点,连接.下列结论:①;②;③;④;⑤.其中正确的有
A.5个 B.4个 C.3个 D.2个
二、填空题(共16分)
11.(4分)在函数中,自变量的取值范围是 .
12.(4分)命题:“如果,那么”的逆命题是 命题(填“真”或“假” .
13.(4分)如图,的周长为26,的垂直平分线交于点,垂足为,若,则的周长是 .
14.(4分)等腰三角形有一内角的度数为,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为 .
三、解答题(共74分)
15.(6分)如图,平面直角坐标系中,已知的三个顶点的坐标分别为,,.
(1)画出关于轴的对称图形△;
(2)画出△向左平移4个单位长度后得到的△;
(3)如果上有一点经过上述两次变换,那么对应上的点的坐标是 .
16.(6分)已知与成正比例,且当时,.
(1)求出与之间的函数解析式;
(2)当时,求的值.
17.(6分)在中,已知,,求的度数.
18.(6分)如图,在和中,点,,,在同一直线上,且,,.求证:.
19.(8分)“中国海监50”在南海海域处巡逻,观测到灯塔在其北偏东的方向上,现该船以每小时10海里的速度沿南偏东的方向航行2小时后到达处,此时测得灯塔在其北偏东的方向上,求货轮到达处时与灯塔的距离.
20.(10分)如图,已知过点的直线与直线相交于点.
(1)求直线的解析式;
(2)求的面积.
(3)根据图象,直接写出的解集.
21.(10分)如图,在中,,点、、分别在、、边上,且,.
(1)求证:是等腰三角形;
(2)当时,求的度数.
22.(10分)某商店销售型和型两种型号的电脑,销售一台型电脑可获利120元,销售一台型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的3倍.设购进型电脑台,这100台电脑的销售总利润为元.
(1)求与的函数关系式,并求出自变量的取值范围;
(2)该商店购进型、型电脑各多少台,才能使销售利润最大?最大利润是多少?
23.(12分)如图,把一块直角三角尺的直角顶点放置在水平直线上,在中,,,试回答下列问题:
(1)若把三角尺绕着点按顺时针方向旋转,当时, 度;
(2)在三角尺绕着点按顺时针方向旋转过程中,分别作于,与,若,,求.
(3)三角尺绕着点按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.
参考答案与解析
一、单选题(共30分)
1.(3分)在平面直角坐标系中,点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据各象限内点的坐标特征解答.
【解答】解:点在第四象限.
故选:.
2.(3分)下面四个交通标志图中为轴对称图形的是
A. B. C. D.
【分析】根据轴对称图形的概念对各选项分析判断即可得解.
【解答】解:、不是轴对称图形,故本选项不符合题意;
、是轴对称图形,故本选项符合题意;
、不是轴对称图形,故本选项不符合题意;
、不是轴对称图形,故本选项不符合题意.
故选:.
3.(3分)点A(﹣5,y1)和B(﹣2,y2)都在直线上,则y1与y2的关系是( )
A.y1≤y2 B.y1=y2 C.y1<y2 D.y1>y2
【分析】由k=>0,利用一次函数的性质可得出y随x的增大而增大,结合﹣5<﹣2,即可得出y1<y2.
【解答】解:∵k=>0,
∴y随x的增大而增大,
又∵点A(﹣5,y1)和B(﹣2,y2)都在直线上,且﹣5<﹣2,
∴y1<y2.
故选:C.
4.(3分)若三条线段中,,为奇数,那么由、、为边组成的三角形共有
A.1个 B.3个 C.无数多个 D.无法确定
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,求得第三边的取值范围,再进一步根据是奇数进行分析求解.
【解答】解:根据三角形的三边关系,得
,.
又是奇数,则或5或7.
故选:.
5.(3分)如图,兔子的三个洞口、、构成,猎狗想捕捉兔子,必须到三个洞口的距离都相等,则猎狗应蹲守在
A.三个角的角平分线的交点 B.三条边的垂直平分线的交点
C.三角形三条高的交点 D.三角形三条中线的交点
【分析】用线段垂直平分线性质判断即可.
【解答】解:猎狗到三个顶点的距离相等,则猎狗应蹲守在的三条边垂直平分线的交点.
故选:.
6.(3分)如图所示,在中,、、分别为、、的中点,且,则的面积等于
A. B. C. D.
【分析】根据三角形中线的性质,先求得的面积,再求得的面积,即可求得的面积.
【解答】解:,为的中点,
,
为的中点,
,
为的中点,
,
故选:.
7.(3分)下列图形中,表示一次函数与正比例函数,为常数,且的图象的是
A. B.
C. D.
【分析】将、与0进行比较,然后分情况讨论其图象的位置.
【解答】解:若,,
则函数图象经过一、二、三象限,函数图象经过一、三象限,
若,,
则函数图象经经过一、三、四象限,函数图象经过二、四象限,
若,
则函数图象经经过二、三、四象限,函数图象经过一、三象限,
若,
则函数图象经经过一、二、四象限,函数图象经过二、四象限,
故选:.
8.(3分)如图,已知,,增加下列条件之一:①;②;③;④.其中能使的条件有
A.1个 B.2个 C.3个 D.4个
【分析】先由得到,然后分别利用“”、“ ”和“”对各添加的条件进行判断.
【解答】解:,
,
,
当时,可根据“”判断;
当时,不能判断;
当时,可根据“”判断;
当时,可根据“”判断.
故选:.
9.(3分)如图,,,,若,则等于
A.12 B.6 C.5 D.4
【分析】过点作于,如图,根据角平分线的性质得到,再利用平行线的性质得到,接着根据含30度的直角三角形三边的关系得到,从而得到的长.
【解答】解:过点作于,如图,
,
平分,,
而,,
,
,
,
,
.
故选:.
10.(3分)如图,为线段上一动点(不与点、重合),在同侧分别作等边三角形和等边三角形,与交于点,与交于点,与交于点,连接.下列结论:①;②;③;④;⑤.其中正确的有
A.5个 B.4个 C.3个 D.2个
【分析】首先利用证明,得,,可说明①④正确;再利用说明,得,由,得是等边三角形,可说明②③正确,由,得,故⑤错误.
【解答】解:、是等边三角形,
,,,
,
,
,,
,
,
故①④正确;
,,,
,
,
,
是等边三角形,
,
,
故②③正确,
,
,
故⑤错误,
正确的有4个,
故选:.
二、填空题(共16分)
11.(4分)在函数中,自变量的取值范围是 且 .
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
【解答】解:根据二次根式有意义,分式有意义得:且,
解得:且.
故答案为且.
12.(4分)命题:“如果,那么”的逆命题是 假 命题(填“真”或“假” .
【分析】直接利用逆命题的写法就是将原命题的结论与题设交换进而得出答案.
【解答】解:命题:“如果,那么”的逆命题是如果,那么,是假命题;
故答案为:假.
13.(4分)如图,的周长为26,的垂直平分线交于点,垂足为,若,则的周长是 16 .
【分析】根据线段垂直平分线的性质得到,,根据三角形的周长公式计算即可.
【解答】解:是的垂直平分线,,
,,
的周长为26,
,
,
的周长,
故答案为:16.
14.(4分)等腰三角形有一内角的度数为,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为 或 .
【分析】根据题意,一种情况为顶角是,根据直角三角形两锐角互余即可推出所求角为,另一种情况为底角是,根据等腰三角形以及三角形内角和定理推出顶角是,再根据直角三角形两锐角互余即可推出所求角为.
【解答】解:①此等腰三角形顶角是,如图1.
在中,,,
;
②此等腰三角形底角是,如图2,
,,
,
.
,
在中,,,
.
综上可知,一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为或.
故答案为:或.
三、解答题(共74分)
15.(6分)如图,平面直角坐标系中,已知的三个顶点的坐标分别为,,.
(1)画出关于轴的对称图形△;
(2)画出△向左平移4个单位长度后得到的△;
(3)如果上有一点经过上述两次变换,那么对应上的点的坐标是 .
【分析】(1)利用轴对称的性质即可画图;
(2)利用平移的性质即可画图;
(3)根据平面直角坐标系中点的变化规律可得出答案.
【解答】解:(1)如图,△即为所求;
(2)如图,△即为所求;
(3)点经过上述两次变换,那么对应上的点的坐标为,
故答案为:.
16.(6分)已知与成正比例,且当时,.
(1)求出与之间的函数解析式;
(2)当时,求的值.
【分析】(1)利用正比例函数的定义,设,然后把已知的一组对应值代入求出即可得到与的关系式;
(2)利用(1)中关系式求出自变量为1时对应的函数值即可.
【解答】解:(1)设,
把,代入得,解得,
所以,
即;
(2)当时,.
17.(6分)在中,已知,,求的度数.
【分析】将第一个等式代入第二等式用表示出,再根据三角形的内角和等于列方程求出,然后求解即可.
【解答】解:,,
,
由三角形内角和定理得,,
所以,,
解得.
18.(6分)如图,在和中,点,,,在同一直线上,且,,.求证:.
【分析】根据等式的性质得出,再利用得出:与全等,进而得出.
【解答】证明:,
,
即,
在与中,
,
,
.
19.(8分)“中国海监50”在南海海域处巡逻,观测到灯塔在其北偏东的方向上,现该船以每小时10海里的速度沿南偏东的方向航行2小时后到达处,此时测得灯塔在其北偏东的方向上,求货轮到达处时与灯塔的距离.
【分析】利用平行线性质得出:,,进而得出,得出是等边三角形,进而得出答案.
【解答】解:由题意得:,(海里),
,
,
,
,
是等边三角形,
海里,
答:货轮到达处时与灯塔的距离为20海里.
20.(10分)如图,已知过点的直线与直线相交于点.
(1)求直线的解析式;
(2)求的面积.
(3)根据图象,直接写出的解集.
【分析】(1)由点在直线上,利用一次函数图象上点的坐标特征,即可求出值,再利用点的坐标和点的坐标可求直线的解析式;
(2)由解析式求得、的坐标,即可求得,然后根据三角形面积公式即可求得;
(3)不等式即的函数值大于的函数值,观察函数图象得到当时满足条件;
【解答】解:(1)点在直线上,
,即,
则的坐标为,
由题意,得,解得:.
的解析式为:;
(2)直线与轴相交于点,
点的坐标为,则,
.
(3)由图象可知,不等式的解集是.
21.(10分)如图,在中,,点、、分别在、、边上,且,.
(1)求证:是等腰三角形;
(2)当时,求的度数.
【分析】(1)根据等边对等角可得,利用“边角边”证明和全等,根据全等三角形对应边相等可得,再根据等腰三角形的定义证明即可;
(2)根据全等三角形对应角相等可得,然后求出,再利用三角形的内角和定理和平角的定义求出.
【解答】(1)证明:,
,
在和中,
,
,
,
是等腰三角形;
(2)解:,
,
,
,
,
,
,,
,
.
22.(10分)某商店销售型和型两种型号的电脑,销售一台型电脑可获利120元,销售一台型电脑可获利140元.该商店计划一次购进两种型号的电脑共100台,其中型电脑的进货量不超过型电脑的3倍.设购进型电脑台,这100台电脑的销售总利润为元.
(1)求与的函数关系式,并求出自变量的取值范围;
(2)该商店购进型、型电脑各多少台,才能使销售利润最大?最大利润是多少?
【分析】(1)用型电脑、型电脑的利润相加,即得与的函数关系式,根据型电脑的进货量不超过型电脑的3倍可得,即可得自变量的取值范围;
(2)根据一次函数的性质即可得答案.
【解答】解:(1)由题意可得,型电脑的总利润为:,型电脑的总利润为:,
、电脑的总利润:,
与的函数关系式为:,
又型电脑的进货量不超过型电脑的3倍,
,
解得:,
自变量的取值范围为:,且为正整数,
,且为正整数);
(2),且,
随的增大而减小,
,且为正整数,
时,有最大值为:,
型电脑进货25台,型电脑进货75台,销售利润最大为13500元.
23.(12分)如图,把一块直角三角尺的直角顶点放置在水平直线上,在中,,,试回答下列问题:
(1)若把三角尺绕着点按顺时针方向旋转,当时, 45 度;
(2)在三角尺绕着点按顺时针方向旋转过程中,分别作于,与,若,,求.
(3)三角尺绕着点按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.
【分析】(1)先求出,再用平行线的性质,即可求出答案;
(2)先用同角的余角相等判断出,同理:,进而判断出,得出,,即可求出答案;
(3)同(2)的方法,即可得出结论.
【解答】解:(1)在中,,,
,
,
,
故答案为45;
(2)于,于,
,.
,
又,
,
同理:,
在和中,
,
,
,,
;
(3),理由:
同(2)的方法得,,
,,
.
同课章节目录
