2.3-2.4不等式的解集一元一次不等式 课件(共42张PPT)
文档属性
| 名称 | 2.3-2.4不等式的解集一元一次不等式 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 21:15:29 | ||
图片预览









文档简介
(共42张PPT)
第二章 一元一次不等式与一元一次不等式组
2.3-2.4不等式的解集 一元一次不等式
2021-2022学年八年级数学下册(北师大版)
1. x = 4,5,6,7.2能使不等式x > 5成立么?
2. 你还能说出几个使不等式x > 5成立的x值吗?你认为不等式 x > 5的解有几个?
问题引入
能使不等式成立的未知数的值叫做不等式的解.
例如,5是不等式 x+1>5的一个解,4.2,6,7,8,···也是它的解.
判断某个数值是不是不等式的解,就用这个数值代替不等式中的未知数,看不等式是否成立.
一、不等式的解集
不等式 x + 1> 5的解集是x > 4.
一个含有未知数的不等式的所有解,组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
练习
判断下列说法是否正确,为什么?
(1)x=2,是不等式 2x < 6的一个解.
(2)x > 1的正整数解有无数个.
(3)因为 x=1是不等式 x – 5 < 0的一个解,
因此该不等式的解为 x = 1.
√
√
×
不等式的解是指满足这个不等式的未知数的某个值,而不等式的解集是指满足这个不等式的未知数的所有值.
不等式的解
不等式的解集
用数轴表示不等式的解集
我们知道数轴上右边的点表示的数总是比左边的点表示的数大可以根据这一特点来描述不等式的解集.
(1)x > a.
a
(2)x ≥ a.
a
(3)x < a.
a
(4)x ≤ a.
a
用数轴确定不等式的解集主要有三个步骤:
(1)画数轴:画出标准数轴.
(2)定边界:根据不等式解集中的数据确定边界.若有等号,则边界点就用实心圆点表示;若没有等号,则边界点就用空心圆圈表示.
(3)根据解集中不等号的方向,确定数轴中表示解集的线的方向,“大于向右,小于向左”.
1.将下列不等式的解集分别表示在数轴上:
(1)x≥4
(2)x≤-1
(3)x>-2
(4)x<6
练一练
2. 不等式 x≥-3的负整数解是_______________ ,
不等式x-1<2的正整数解是_____________________.
-3、-2、-1
1、2
合作探究
思考
观察下面的不等式:
x-7>26
3x-7>26
-4x>3
它们有哪些共同特征?
每个不等式都只含有一个未知数;并且未知数的次数是1.
二、一元一次不等式的概念
只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
概括总结
练一练
下列不等式中,哪些是一元一次不等式
(1) 3x+2>x–1 (2)5x+3<0
(3) (4)x(x–1)<2x
左边不是整式
化简后是
x2-x<2x
合作探究
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
三、解一元一次不等式
归纳总结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为xa的形式.
例1 解下列一元一次不等式 :
(1) 2-5x < 8-6x ;
(2) .
解:
(1) 原不等式为2-5x < 8-6x
将同类项放在一起
即 x < 6.
移项,得 -5x+6x < 8-2,
计算结果
典例精析
解:
首先将分母去掉
去括号,得 2x -10 + 6 ≤ 9x
去分母,得 2(x -5)+1×6 ≤ 9x
移项,得 2x - 9x ≤ 10 - 6
去括号
将同类项放在一起
(2) 原不等式为
合并同类项,得 -7x ≤ 4
两边都除以-7,得
x ≥ .
计算结果
根据不等式性质3
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
1.(1)解不等式3(x+2)-8≥1-2(x-1),并把它的解集表示在数轴上.
解:去括号,得3x+6-8≥1-2x+2.
移项,得3x+2x≥1+2-6+8.
合并同类项,得5x≥5.
系数化为1,得x≥1.
在数轴上表示为:
练一练
解:去分母,得4(2x-1)≤3(3x+2)-12.
去括号,得8x-4≤9x+6-12.
移项,得8x-9x≤6-12+4.
合并同类项,得-x≤-2.
把x的系数化为1,得x≥2.
在数轴上表示为:
2.求不等式3(x+1)≥5x-9的正整数解.
解:去括号,得3x+3≥5x-9.
移项,得3x-5x≥-9-3.
合并同类项,得-2x≥-12.
系数化为1,得x≤6.
所以不等式3(x+1)≥5x-9的正整数解是1,2,3,4,5,6.
问题:小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
三、一元一次不等式的应用
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
例1 某种商品进价为200元,标价为300元出售,商场规定可以打折销售,但其利润率不能少于5%. 请你帮助售货员计算一下,这种商品最多可以按几折销售?
解: 设该商品可以打 x 折销售.
则 (300×0.1x-200)÷200≥5%.
解得
x ≥ 7.
答:这种商品最多可以按七折销售.
分析: 本题涉及的数量关系是:
(出售价-进价)÷进价≥利润率.
典例精析
例2 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解: 设小明答对了 x 道题,则他答错和不答
的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
分析: 本题涉及的数量关系是:总得分≥85.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
1. 若代数式 的值是非负数,则 x 的取值范围是( )
A.x≥ B.x≥
C.x> D.x>
B
课堂练习
2.如图所示,图中阴影部分表示 x 的取值范围,则下列表示中正确的是( )
B
A.-3>x>2 B.-3<x≤2
C.-3≤x≤2 D.-3<x<2
3.当x或y满足什么条件时,下列关系成立?
(1)2(x+1)大于或等于1;
(2)4x与7的和不小于6;
根据题意,得不等式2(x+1)≥1,解得x≥- .
根据题意,得不等式4x+7≥6,解得x≥- .
(3)y与1的差不大于2y与3的差;
(4)3y与7的和的四分之一小于-2.
根据题意,得不等式y-1≤2y-3,解得y≥2.
根据题意,得不等式 <-2,解得y<-5.
4.解下列不等式,并把它们的解集在数轴上表示出来.
(1)3(2x+5)>2(4x+3);
(2) ;
(3) .
(1)3(2x+5)>2(4x+3)
6x+15>8x+6
解:
x<
用数轴
表示为
(2)
用数轴
表示为
3x-9<4x-10
解:
x>1
(3)
用数轴
表示为
2y+2-3(2y-5)≥12
解:
y≤
5. 某商店以每辆 250 元的进价购入 200 辆自行车,并以每辆 275 元的价格销售,两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
解:设这时已售出 x 辆自行车.
由题意得:275x>250×200,
解得 x> .
又∵x 为正整数. ∴x≥182.
答:这时至少已售出 182 辆自行车.
6. 长跑比赛中,张华跑在前面,在离终点100 m 时他以 4 m/s 的速度向终点冲刺,在他身后 10 m 的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?
解:设李明以 x m/s 的速度冲刺.
由题意得: x>100+10 .
解得 x>4.4.
答:李明需以超过 4.4 m/s 的速度冲刺,才能在张华之前到达终点.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第二章 一元一次不等式与一元一次不等式组
2.3-2.4不等式的解集 一元一次不等式
2021-2022学年八年级数学下册(北师大版)
1. x = 4,5,6,7.2能使不等式x > 5成立么?
2. 你还能说出几个使不等式x > 5成立的x值吗?你认为不等式 x > 5的解有几个?
问题引入
能使不等式成立的未知数的值叫做不等式的解.
例如,5是不等式 x+1>5的一个解,4.2,6,7,8,···也是它的解.
判断某个数值是不是不等式的解,就用这个数值代替不等式中的未知数,看不等式是否成立.
一、不等式的解集
不等式 x + 1> 5的解集是x > 4.
一个含有未知数的不等式的所有解,组成这个不等式的解集.
求不等式解集的过程叫做解不等式.
练习
判断下列说法是否正确,为什么?
(1)x=2,是不等式 2x < 6的一个解.
(2)x > 1的正整数解有无数个.
(3)因为 x=1是不等式 x – 5 < 0的一个解,
因此该不等式的解为 x = 1.
√
√
×
不等式的解是指满足这个不等式的未知数的某个值,而不等式的解集是指满足这个不等式的未知数的所有值.
不等式的解
不等式的解集
用数轴表示不等式的解集
我们知道数轴上右边的点表示的数总是比左边的点表示的数大可以根据这一特点来描述不等式的解集.
(1)x > a.
a
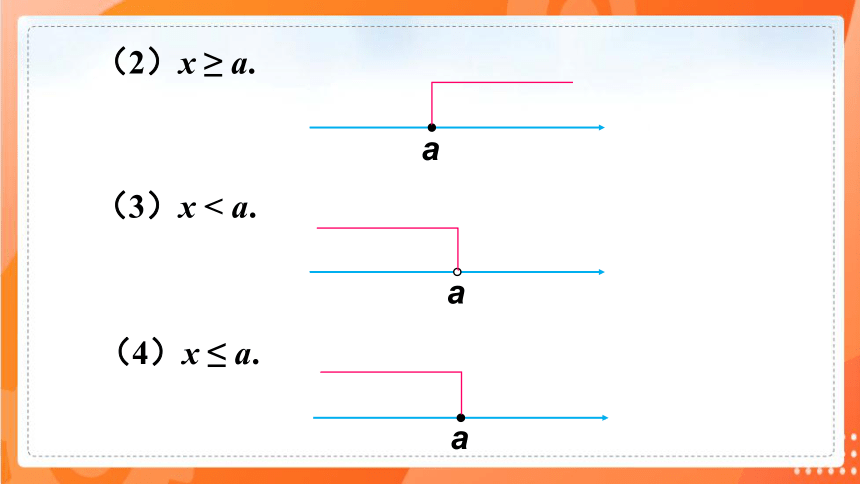
(2)x ≥ a.
a
(3)x < a.
a
(4)x ≤ a.
a
用数轴确定不等式的解集主要有三个步骤:
(1)画数轴:画出标准数轴.
(2)定边界:根据不等式解集中的数据确定边界.若有等号,则边界点就用实心圆点表示;若没有等号,则边界点就用空心圆圈表示.
(3)根据解集中不等号的方向,确定数轴中表示解集的线的方向,“大于向右,小于向左”.
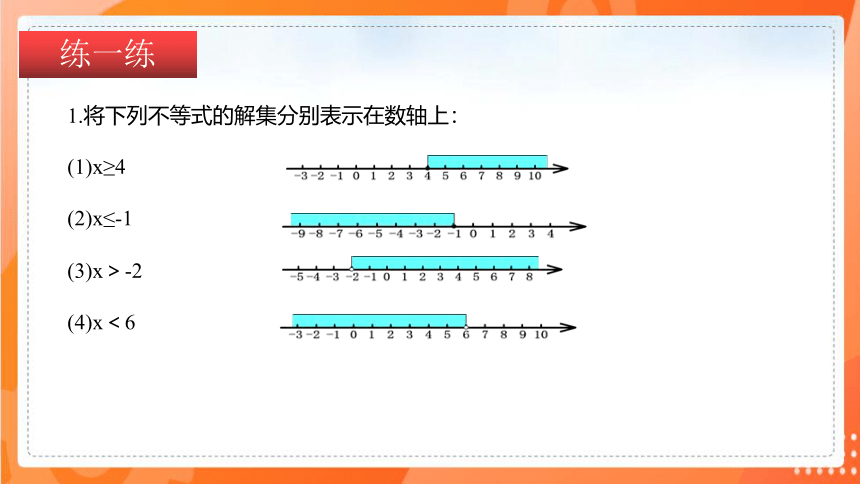
1.将下列不等式的解集分别表示在数轴上:
(1)x≥4
(2)x≤-1
(3)x>-2
(4)x<6
练一练
2. 不等式 x≥-3的负整数解是_______________ ,
不等式x-1<2的正整数解是_____________________.
-3、-2、-1
1、2
合作探究
思考
观察下面的不等式:
x-7>26
3x-7>26
-4x>3
它们有哪些共同特征?
每个不等式都只含有一个未知数;并且未知数的次数是1.
二、一元一次不等式的概念
只含一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
一元一次不等式的定义
概括总结
练一练
下列不等式中,哪些是一元一次不等式
(1) 3x+2>x–1 (2)5x+3<0
(3) (4)x(x–1)<2x
左边不是整式
化简后是
x2-x<2x
合作探究
解不等式:
4x-1<5x+15
解方程:
4x-1=5x+15
解:移项,得
4x-5x=15+1
合并同类项,得
-x=16
系数化为1,得
x=-16
解:移项,得
4x-5x<15+1
合并同类项,得
-x<16
系数化为1,得
x>-16
三、解一元一次不等式
归纳总结
解一元一次方程,要根据等式的性质,将方程逐步化为x=a的形式;而解一元一次不等式,则要根据不等式的性质,将不等式逐步化为x
例1 解下列一元一次不等式 :
(1) 2-5x < 8-6x ;
(2) .
解:
(1) 原不等式为2-5x < 8-6x
将同类项放在一起
即 x < 6.
移项,得 -5x+6x < 8-2,
计算结果
典例精析
解:
首先将分母去掉
去括号,得 2x -10 + 6 ≤ 9x
去分母,得 2(x -5)+1×6 ≤ 9x
移项,得 2x - 9x ≤ 10 - 6
去括号
将同类项放在一起
(2) 原不等式为
合并同类项,得 -7x ≤ 4
两边都除以-7,得
x ≥ .
计算结果
根据不等式性质3
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
议一议
1.(1)解不等式3(x+2)-8≥1-2(x-1),并把它的解集表示在数轴上.
解:去括号,得3x+6-8≥1-2x+2.
移项,得3x+2x≥1+2-6+8.
合并同类项,得5x≥5.
系数化为1,得x≥1.
在数轴上表示为:
练一练
解:去分母,得4(2x-1)≤3(3x+2)-12.
去括号,得8x-4≤9x+6-12.
移项,得8x-9x≤6-12+4.
合并同类项,得-x≤-2.
把x的系数化为1,得x≥2.
在数轴上表示为:
2.求不等式3(x+1)≥5x-9的正整数解.
解:去括号,得3x+3≥5x-9.
移项,得3x-5x≥-9-3.
合并同类项,得-2x≥-12.
系数化为1,得x≤6.
所以不等式3(x+1)≥5x-9的正整数解是1,2,3,4,5,6.
问题:小华打算在星期天与同学去登山,计划上午7点出发,到达山顶后休息2h,下午4点以前必须回到出发点. 如果他们去时的平均速度是3km/h,回来时的平均速度是4km/h,他们最远能登上哪座山顶(图中数字表示出发点到山顶的路程)?
三、一元一次不等式的应用
前面问题中涉及的数量关系是:
去时所花时间+休息时间+回来所花时间≤总时间.
解:设从出发点到山顶的距离为x km,
则他们去时所花时间为 h
回来所花时间为 h.
他们在山顶休息了2 h,又上午7点到下午4点之间总共相隔9 h,即所用时间应小于或等于9 h.
所以有 +2+ ≤ 9.
解得 x≤12.
因此要满足下午4点以前必须返回出发点,小华他们最远能登上D山顶.
例1 某种商品进价为200元,标价为300元出售,商场规定可以打折销售,但其利润率不能少于5%. 请你帮助售货员计算一下,这种商品最多可以按几折销售?
解: 设该商品可以打 x 折销售.
则 (300×0.1x-200)÷200≥5%.
解得
x ≥ 7.
答:这种商品最多可以按七折销售.
分析: 本题涉及的数量关系是:
(出售价-进价)÷进价≥利润率.
典例精析
例2 一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答对了几道题?
解: 设小明答对了 x 道题,则他答错和不答
的共有 (25-x)道题.根据题意,得
4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
答:小明至少答对了22道题.
分析: 本题涉及的数量关系是:总得分≥85.
应用一元一次不等式解决实际问题的步骤:
实际问题
解不等式
列不等式
结合实际
确定答案
找出不等关系
设未知数
总结归纳
1. 若代数式 的值是非负数,则 x 的取值范围是( )
A.x≥ B.x≥
C.x> D.x>
B
课堂练习
2.如图所示,图中阴影部分表示 x 的取值范围,则下列表示中正确的是( )
B
A.-3>x>2 B.-3<x≤2
C.-3≤x≤2 D.-3<x<2
3.当x或y满足什么条件时,下列关系成立?
(1)2(x+1)大于或等于1;
(2)4x与7的和不小于6;
根据题意,得不等式2(x+1)≥1,解得x≥- .
根据题意,得不等式4x+7≥6,解得x≥- .
(3)y与1的差不大于2y与3的差;
(4)3y与7的和的四分之一小于-2.
根据题意,得不等式y-1≤2y-3,解得y≥2.
根据题意,得不等式 <-2,解得y<-5.
4.解下列不等式,并把它们的解集在数轴上表示出来.
(1)3(2x+5)>2(4x+3);
(2) ;
(3) .
(1)3(2x+5)>2(4x+3)
6x+15>8x+6
解:
x<
用数轴
表示为
(2)
用数轴
表示为
3x-9<4x-10
解:
x>1
(3)
用数轴
表示为
2y+2-3(2y-5)≥12
解:
y≤
5. 某商店以每辆 250 元的进价购入 200 辆自行车,并以每辆 275 元的价格销售,两个月后自行车的销售款已超过这批自行车的进货款,这时至少已售出多少辆自行车?
解:设这时已售出 x 辆自行车.
由题意得:275x>250×200,
解得 x> .
又∵x 为正整数. ∴x≥182.
答:这时至少已售出 182 辆自行车.
6. 长跑比赛中,张华跑在前面,在离终点100 m 时他以 4 m/s 的速度向终点冲刺,在他身后 10 m 的李明需以多快的速度同时开始冲刺,才能够在张华之前到达终点?
解:设李明以 x m/s 的速度冲刺.
由题意得: x>100+10 .
解得 x>4.4.
答:李明需以超过 4.4 m/s 的速度冲刺,才能在张华之前到达终点.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
