2021—2022学年度人教版九年级数学下册27.2.1相似三角形的判定课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年度人教版九年级数学下册27.2.1相似三角形的判定课后练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 461.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 10:21:44 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似 27.2.1
相似三角形的判定课后练习
一、选择题
1.下列各组条件中,一定能够判定△ABC与△DEF相似的是( )
A.∠A=∠B,∠D=∠E
B.∠B=∠E,AB=3,AC=4,DE:DF=3:4
C.△ABC三边长分别为6,18,21,△DEF三边之比为2:7:6
D.∠C=91°,∠E=91°,DE:AB=EF:AC
2.在下列条件中,不能判断与相似的是( )
A. B.且
C. D.=且
3.如图,下列不能判定与相似的是( )
A. B. C. D.
4.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B.
C. D.
5.如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
6.如图,下列条件不能判定与相似的是( )
A. B.
C. D.
7.如图,,交于点O,有下列三个结论:①,②,③.则一定成立的有( ).
A.0个 B.1个 C.2个 D.3个
8.如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成,且,则线段BE的长为( )
A. B. C. D.
9.如图,在中,是边上一点,在边上求作一点,使得.甲的作法:过点作,交于点,则点即为所求.乙的作法:经过点,,作,交于点,则点即为所求.对于甲、乙的作法,下列判断正确的是( )
A.甲错误,乙正确 B.甲正确,乙错误 C.甲、乙都错误 D.甲、乙都正确
10.如图,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是( )
A.△BFE B.△AFD C.△ACE D.△BAE
二、填空题
11.在和中,,,,,则__时,和相似.
12.如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有_____对.
13.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
14.如图,,,在、、、、、中写出一对相似三角形______________.
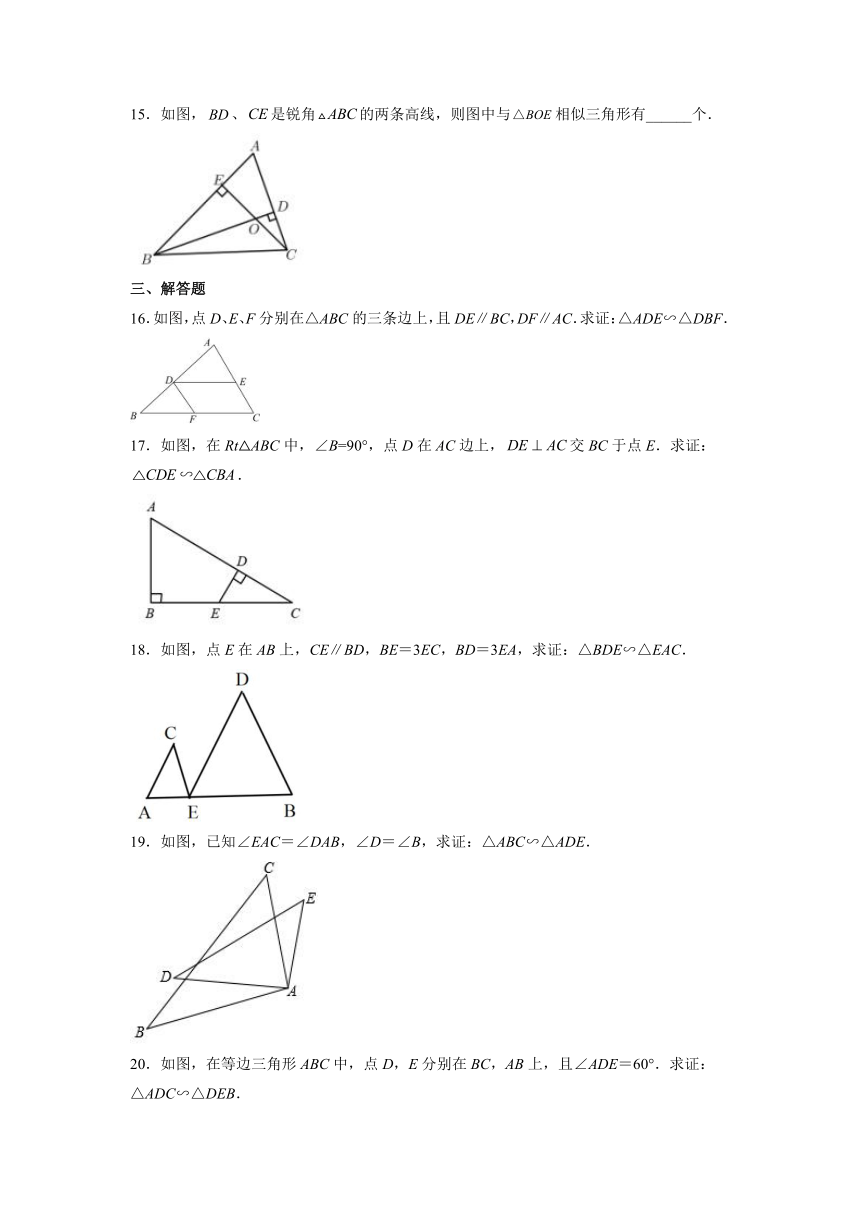
15.如图,、是锐角的两条高线,则图中与相似三角形有______个.
三、解答题
16.如图,点D、E、F分别在△ABC的三条边上,且DE∥BC,DF∥AC.求证:△ADE∽△DBF.
17.如图,在Rt△ABC中,∠B=90°,点D在AC边上,交BC于点E.求证:.
18.如图,点E在AB上,CE∥BD,BE=3EC,BD=3EA,求证:△BDE∽△EAC.
19.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
20.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB.
21.如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD的延长线上,且满足∠MAN=90°,连接MN、AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AN2=AE AC.
22.如图所示,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F.
(1)求证:△BEF∽△CDF;
(2)求证:DE·BF=EF·BC.
23.如图1,二次函数的图像记为,与y轴交于点A,其顶点为B,二次函数的图像记为,其顶点为D,图像、相交于点P,设点P的横坐标为m.
(1)求证:点D在直线上;
(2)求m和h的数量关系;
(3)平行于x轴的直线经过点P,与图像交于另一点E,与图像交于另一点F,若,求h的值;
(4)如图2,过点P作平行于的直线,与图像交于另一点Q,连接.当时,_________.(直接写出结果)
【参考答案】
1.C 2.B 3.A 4.C 5.B 6.A 7.D 8.D 9.A 10.D
11.或
12.3
13.①③④
14.
15.3
16.证明:∵DE∥BC,DF∥AC,
∴∠ADE=∠DBF,∠AED=∠C,∠DFB=∠C,
∴∠AED=∠DFB,
∴△ADE∽△DBF.
17.∵,∠B=90°,
∴.
又∵∠C=∠C,
∴.
18.∵CE//BD,
∴∠CEA=∠B,
∵BE=3EC,BD=3EA,
∴,
∴ △BDE∽△EAC.
19.解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
20.证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠ADB=∠1+∠C=∠1+60°,
∵∠ADE=60°,
∴∠ADB=∠2+60°,
∴∠1=∠2,
∴△ADC∽△DEB.
21.(1)四边形ABCD是正方形,
,
∠MAN=90°,
,
,
,
,
.
(2),,
,
四边形ABCD是正方形,
,
,
∠CAD=2∠NAD,
,
,
,
,
,
,,
,
,
.
22.证明:证明:(1),,
,且,
;
(2)如图,连接,
,
点,点,点,点四点共圆,
,,
,
,
23.(1)证明:由,
令x=0时,y=1,即A(0,1),令y=0时,x=2,即B(2,0),
设A,B的解析式为: ,
把A,B的坐标代入得,解得,
∴顶点D的坐标为,
令x=h,则 ,
∴点D在直线上;
(2)联立 ,
得出,
根据图象交于点P,
设点P的横坐标为m,则;
(3)由点P的横坐标为x=,代入,得出E点的横坐标为4-,
将P的横坐标为x=,代入得出F点的横坐标为,
则,
解得h=8;
(4)由题意得由平移得到,
∴BD=PQ且BD∥PQ,得出四边形BPQD为矩形,
作DM⊥x轴,得出△AOB∽△BMP,当h=4时,一定成立;
又有 ,得出h=20,
综上所述h=4或20.
相似三角形的判定课后练习
一、选择题
1.下列各组条件中,一定能够判定△ABC与△DEF相似的是( )
A.∠A=∠B,∠D=∠E
B.∠B=∠E,AB=3,AC=4,DE:DF=3:4
C.△ABC三边长分别为6,18,21,△DEF三边之比为2:7:6
D.∠C=91°,∠E=91°,DE:AB=EF:AC
2.在下列条件中,不能判断与相似的是( )
A. B.且
C. D.=且
3.如图,下列不能判定与相似的是( )
A. B. C. D.
4.如图,点D、E分别在的边AB、AC的反向延长线上,下面比例式中,不一定能判断的是( )
A. B.
C. D.
5.如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
6.如图,下列条件不能判定与相似的是( )
A. B.
C. D.
7.如图,,交于点O,有下列三个结论:①,②,③.则一定成立的有( ).
A.0个 B.1个 C.2个 D.3个
8.如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成,且,则线段BE的长为( )
A. B. C. D.
9.如图,在中,是边上一点,在边上求作一点,使得.甲的作法:过点作,交于点,则点即为所求.乙的作法:经过点,,作,交于点,则点即为所求.对于甲、乙的作法,下列判断正确的是( )
A.甲错误,乙正确 B.甲正确,乙错误 C.甲、乙都错误 D.甲、乙都正确
10.如图,在△ABC中,BD⊥AC于点D,AE⊥BC于点E,交BD于点F,下列三角形中不一定与△BCD相似的是( )
A.△BFE B.△AFD C.△ACE D.△BAE
二、填空题
11.在和中,,,,,则__时,和相似.
12.如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有_____对.
13.如图,在与中,,,,交于点D,给出下列结论.①;②;③;④.其中正确的结论是__________(填写正确结论的序号).
14.如图,,,在、、、、、中写出一对相似三角形______________.
15.如图,、是锐角的两条高线,则图中与相似三角形有______个.
三、解答题
16.如图,点D、E、F分别在△ABC的三条边上,且DE∥BC,DF∥AC.求证:△ADE∽△DBF.
17.如图,在Rt△ABC中,∠B=90°,点D在AC边上,交BC于点E.求证:.
18.如图,点E在AB上,CE∥BD,BE=3EC,BD=3EA,求证:△BDE∽△EAC.
19.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
20.如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°.求证:△ADC∽△DEB.
21.如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD的延长线上,且满足∠MAN=90°,连接MN、AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AN2=AE AC.
22.如图所示,△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD与CE相交于点F.
(1)求证:△BEF∽△CDF;
(2)求证:DE·BF=EF·BC.
23.如图1,二次函数的图像记为,与y轴交于点A,其顶点为B,二次函数的图像记为,其顶点为D,图像、相交于点P,设点P的横坐标为m.
(1)求证:点D在直线上;
(2)求m和h的数量关系;
(3)平行于x轴的直线经过点P,与图像交于另一点E,与图像交于另一点F,若,求h的值;
(4)如图2,过点P作平行于的直线,与图像交于另一点Q,连接.当时,_________.(直接写出结果)
【参考答案】
1.C 2.B 3.A 4.C 5.B 6.A 7.D 8.D 9.A 10.D
11.或
12.3
13.①③④
14.
15.3
16.证明:∵DE∥BC,DF∥AC,
∴∠ADE=∠DBF,∠AED=∠C,∠DFB=∠C,
∴∠AED=∠DFB,
∴△ADE∽△DBF.
17.∵,∠B=90°,
∴.
又∵∠C=∠C,
∴.
18.∵CE//BD,
∴∠CEA=∠B,
∵BE=3EC,BD=3EA,
∴,
∴ △BDE∽△EAC.
19.解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
20.证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∴∠ADB=∠1+∠C=∠1+60°,
∵∠ADE=60°,
∴∠ADB=∠2+60°,
∴∠1=∠2,
∴△ADC∽△DEB.
21.(1)四边形ABCD是正方形,
,
∠MAN=90°,
,
,
,
,
.
(2),,
,
四边形ABCD是正方形,
,
,
∠CAD=2∠NAD,
,
,
,
,
,
,,
,
,
.
22.证明:证明:(1),,
,且,
;
(2)如图,连接,
,
点,点,点,点四点共圆,
,,
,
,
23.(1)证明:由,
令x=0时,y=1,即A(0,1),令y=0时,x=2,即B(2,0),
设A,B的解析式为: ,
把A,B的坐标代入得,解得,
∴顶点D的坐标为,
令x=h,则 ,
∴点D在直线上;
(2)联立 ,
得出,
根据图象交于点P,
设点P的横坐标为m,则;
(3)由点P的横坐标为x=,代入,得出E点的横坐标为4-,
将P的横坐标为x=,代入得出F点的横坐标为,
则,
解得h=8;
(4)由题意得由平移得到,
∴BD=PQ且BD∥PQ,得出四边形BPQD为矩形,
作DM⊥x轴,得出△AOB∽△BMP,当h=4时,一定成立;
又有 ,得出h=20,
综上所述h=4或20.
