冀教版数学七年级下9.2.1 三角形的内角和 课件(共37张PPT)
文档属性
| 名称 | 冀教版数学七年级下9.2.1 三角形的内角和 课件(共37张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
9.2 三角形的内角和外角
第九章 二元一方程组
第1课时 三角形的内角和
课时导入
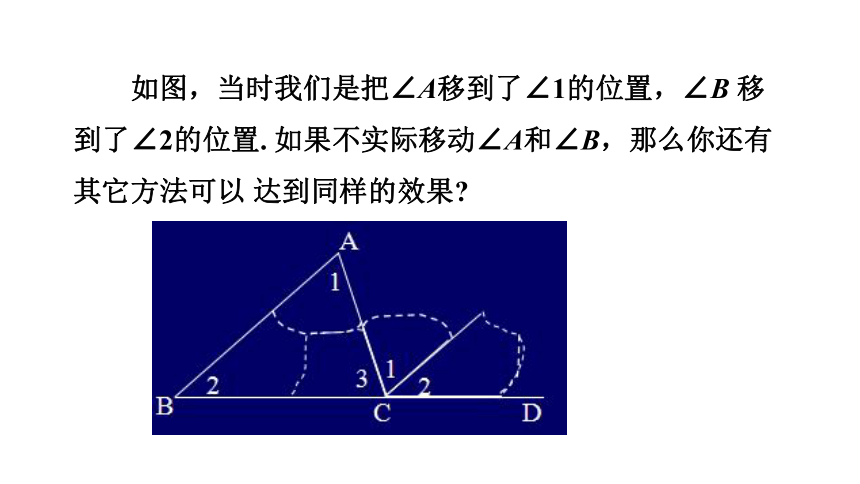
如图,当时我们是把∠A移到了∠1的位置,∠B 移
到了∠2的位置. 如果不实际移动∠A和∠B,那么你还有
其它方法可以 达到同样的效果
知识点
三角形内角和定理
知1-讲
感悟新知
1
三角形内角和的推导方法:
如图,△ABC中,延长BC到
点D,过点画CM∥AB.
所以∠1=∠A,
(两直线平行,内错角相等).
∠2=∠B, (两直线平行,同位角相等).
知1-讲
感悟新知
因为∠1+∠2+∠ACB=180°(平角定义).
所以∠A+∠B+∠ACB=180°(等量代换).
知1-讲
总 结
感悟新知
三角形内角和定理
三角形的内角和等于180°.
知1-讲
感悟新知
特别解读
1.三角形内角和定理揭示了三角形三个内角之间的数量关系.
2.三角形的三个内角中最多只有一个钝角或直角,或者说至
少有两个锐角.
特别提醒
说明三角形内角和定理的思路:
主要是以平行线作为桥梁,将三个内角“转移”集中成一个角或两个角,再说明这个角或两个角的和是180°即可.
感悟新知
知1-练
例 1
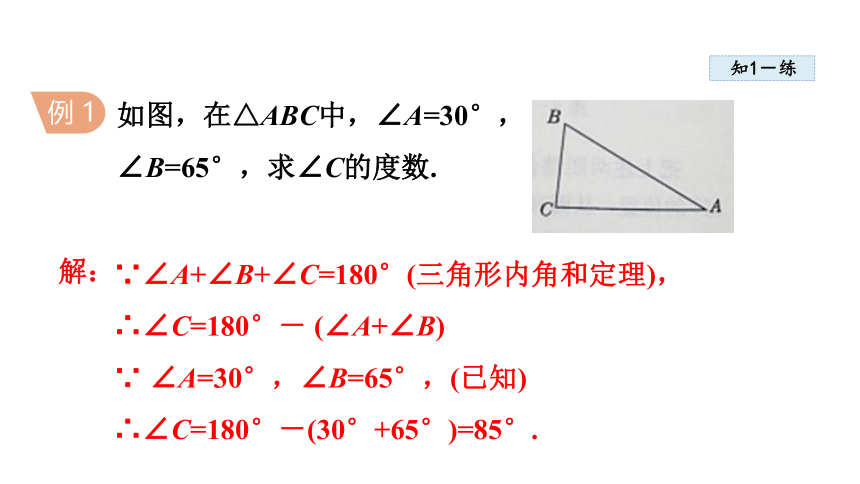
如图,在△ABC中,∠A=30°,∠B=65°,求∠C的度数.
∵∠A+∠B+∠C=180°(三角形内角和定理),
∴∠C=180°- (∠A+∠B)
∵ ∠A=30°,∠B=65°,(已知)
∴∠C=180°-(30°+65°)=85°.
解:
知1-讲
总 结
感悟新知
三角形的内角和是180°是一个隐含条件,以后
经常遇到这种情况,我们需要注意.
感悟新知
知1-练
1.
解:
在△ABC中,∠B=62°24′,∠C=28°52′,求∠A的度数.
因为∠A+∠B+∠C=180°,所以∠A=180°-∠B-∠C=180°-62°24′-28°52′=88°44′.
感悟新知
知1-练
2.
在△ABC中:
(1)若∠C=90°,∠A=25°,求∠B的度数.
(2)若∠C=37°26′,∠A=∠B,求∠A的度数.
(3)若∠A= ∠B= ∠C,求∠C的度数.
感悟新知
知1-练
解:
(1)由已知得∠B=180°-90°-25°=65°.
(2)因为∠C=37°26′,∠A=∠B,所以2∠A+37°26′=180°,解得∠A=71°17′.
(3)因为∠A= ∠B= ∠C,所以设∠A=x,则
∠B=2x,∠C=3x,所以x+2x+3x=180°,解得x=30°,所以∠C=90°.
感悟新知
知1-练
3.
在△ABC中,∠A-∠C=35°,∠B-∠A=5°,求△ABC各内角的度数.
由已知,可得∠C=∠A-35°,∠B=∠A+5°.又因为∠A+∠B+∠C=180°,所以∠A+∠A+5°+∠A-35°=180°,即3∠A-30°=180°,解得∠A=70°.所以∠B=70°+5°=75°,∠C=70°-35°=35°.
解:
感悟新知
知1-练
4.
在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
C
感悟新知
知1-练
5.
在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
D
感悟新知
知1-练
6.
在△ABC中,已知∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60°
C.80° D.90°
A
感悟新知
知1-练
7.
在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( )
A.45° B.60°
C.75° D.90°
C
知识点
三角形的分类
知2-练
感悟新知
2
例2
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,试判断△ABC的形状,并说明理由.
引用辅助量x°,用x°表示出△ABC的三个
内角,在△ABC中,运用三角形内角和定理
构造方程,解方程后,求出△ABC中各角的
度数,再判断△ABC的形状.
导引:
感悟新知
知2-练
解:
△ABC是直角三角形.理由如下:
∵∠A∶∠B∶∠C=1∶2∶3,
∴可设∠A,∠B,∠C的度数分别为x°,2x°,3x°.在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°),
∴x+2x+3x=180,解得x=30.
∴∠C=3x°=90°,
∴△ABC是直角三角形.
知2-讲
总 结
感悟新知
判断一个三角形的形状的方法:(1)可以看三角形中最大的角的大小:最大角是锐角,三角形就是锐角三角形;最大角是直角,三角形就是直角三角形;最大角是钝角,三角形就是钝角三角形.(2)也可以通过角的比判断:两较小角的份数和小于最大角的份数,则此三角形为钝角三角形;两较小角的份数和等于最大角的份数(两锐角互余),则此三角形为直角三角形;两较小角的份数和大于最大角的份数,则此三角形为锐角三角形.
感悟新知
知2-练
1.
解:
在△ABC中,∠C=36°,∠A与∠B的比是1∶2,求∠A,∠B的度数.
因为∠A与∠B的比是1∶2,所以∠B=2∠A,
因为∠A+∠B+∠C=180°,∠C=36°,
所以∠A+2∠A+36°=180°,
解得∠A=48°,所以∠B=96°.
2.
感悟新知
知2-练
一个三角形三个内角的度数之比为2∶3∶7,求这个三角形的三个内角 的度数.
由题意可设这个三角形的三个内角的度数分别为2x,3x,7x,所以2x+3x+7x=180°,解得x=15°,所以2x=30°,3x=45°,7x=105°,所以这个三角形的三个内角的度数分别为30°,45°,105°.
解:
感悟新知
知2-练
例 3
如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向.
(1)试说明△ABC为直角三角形;
(2)求∠BCA的度数.
感悟新知
知2-练
(1)如图,过A作AF∥BD,∴∠BAF=∠ABD=40°.显然AF∥EC,∴∠CAF=∠ECA=50°.∴∠BAC=∠BAF+∠CAF=40°+50°=90°.∴△ABC为直角三角形.
(2)∵∠DBC=75°,∠DBA=40°,∴∠ABC=∠DBC-∠DBA=75°-40°=35°.∴在Rt△ABC中,∠BCA=90°-∠ABC=90°-35°=55°.
解:
知2-讲
总 结
感悟新知
本例主要考查建模思想,即把方位角建模成几何
图形中的角,同时应用了平行线的性质,三角形的内
角和及直角三角形的判定等.
1.
感悟新知
知2-练
解:
在△ABC中,∠C=42°,∠A=∠B,求∠B的度数.
因为∠C=42°,∠A=∠B,所以2∠B+42°=180°,解得∠B=69°.
2.
感悟新知
知2-练
求适合下列条件的△ABC的各内角的度数:
(1)∠A=∠B=30°;
(2)∠A=∠B=∠C;
(3)∠A=50°,∠A+∠B=∠C.
感悟新知
知2-练
在△ABC中,∠A+∠B+∠C=180°.
(1)因为∠A=∠B=30°,所以∠C=180°-30°-30°=120°.
(2)因为∠A=∠B=∠C,所以3∠A=3∠B=3∠C=180°,所以∠A=∠B=∠C=60°.
(3)因为∠A+∠B=∠C,所以2∠C=180°,∠C=90°.因为∠A=50°,所以∠B=180°-∠C-∠A=180°-90°-50°=40°.
解:
3.
感悟新知
知2-练
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC,若∠A=62°,∠AED=54°,则∠B的大小为( )
A.54° B.62°
C.64° D.74°
C
4.
感悟新知
知2-练
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
A.30° B.35°
C.40° D.50°
C
5.
感悟新知
知2-练
直角三角尺和直尺如图放置.若∠1=20°,则∠2的度数为( )
A.60° B.50°
C.40° D.30°
C
6.
感悟新知
知2-练
如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118° B.119°
C.120° D.121°
C
7.
感悟新知
知2-练
如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38°
C.48° D.88°
C
8.
感悟新知
知2-练
将一副三角尺如图放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠1的度数为( )
A.75° B.65°
C.45° D.30°
C
课堂小结
三角形的内角和
知识总结
知识方法要点 关键总结 注意事项
三角形的内角和的定义 三角形的内角和等于180°. 注意单位度的符号是“°”
方法规律总结
(1)三角形是最常见的几何图形之一,在现实生活中有广泛的应用.学习时要注意多联系生活实际,学用结合. (2)在学习过程中,要注意知识之间的相互联系,尤其是前后知识间的因果关系,如借助平行线的性质推导出了三角形的内角和定理.
课堂小结
如图,说明∠A+∠B+∠C与∠ADC之间的关系.
易错点:非三角形问题用内角和定理而致错
三角形的内角和
课堂小结
解:
连接BD.∵∠A+∠ABD+∠ADB=180°,
∠C+∠DBC+∠CDB=180°,
∴∠A+∠ABD+∠ADB+∠C+∠DBC+∠CDB=360°,
又∵∠ADB+∠CDB+∠ADC=360°,
∴∠A+∠ABC+∠C+360°-∠ADC=360°,
∴∠A+∠ABC+∠C=∠ADC.
三角形的内角和
课堂小结
点拨:
连接BD,构成了△ABD和△BDC.本题易忽视四边形ABCD不是三角形,而错误地认为∠A+∠B+∠C=180°>∠ADC.
三角形的内角和
9.2 三角形的内角和外角
第九章 二元一方程组
第1课时 三角形的内角和
课时导入
如图,当时我们是把∠A移到了∠1的位置,∠B 移
到了∠2的位置. 如果不实际移动∠A和∠B,那么你还有
其它方法可以 达到同样的效果
知识点
三角形内角和定理
知1-讲
感悟新知
1
三角形内角和的推导方法:
如图,△ABC中,延长BC到
点D,过点画CM∥AB.
所以∠1=∠A,
(两直线平行,内错角相等).
∠2=∠B, (两直线平行,同位角相等).
知1-讲
感悟新知
因为∠1+∠2+∠ACB=180°(平角定义).
所以∠A+∠B+∠ACB=180°(等量代换).
知1-讲
总 结
感悟新知
三角形内角和定理
三角形的内角和等于180°.
知1-讲
感悟新知
特别解读
1.三角形内角和定理揭示了三角形三个内角之间的数量关系.
2.三角形的三个内角中最多只有一个钝角或直角,或者说至
少有两个锐角.
特别提醒
说明三角形内角和定理的思路:
主要是以平行线作为桥梁,将三个内角“转移”集中成一个角或两个角,再说明这个角或两个角的和是180°即可.
感悟新知
知1-练
例 1
如图,在△ABC中,∠A=30°,∠B=65°,求∠C的度数.
∵∠A+∠B+∠C=180°(三角形内角和定理),
∴∠C=180°- (∠A+∠B)
∵ ∠A=30°,∠B=65°,(已知)
∴∠C=180°-(30°+65°)=85°.
解:
知1-讲
总 结
感悟新知
三角形的内角和是180°是一个隐含条件,以后
经常遇到这种情况,我们需要注意.
感悟新知
知1-练
1.
解:
在△ABC中,∠B=62°24′,∠C=28°52′,求∠A的度数.
因为∠A+∠B+∠C=180°,所以∠A=180°-∠B-∠C=180°-62°24′-28°52′=88°44′.
感悟新知
知1-练
2.
在△ABC中:
(1)若∠C=90°,∠A=25°,求∠B的度数.
(2)若∠C=37°26′,∠A=∠B,求∠A的度数.
(3)若∠A= ∠B= ∠C,求∠C的度数.
感悟新知
知1-练
解:
(1)由已知得∠B=180°-90°-25°=65°.
(2)因为∠C=37°26′,∠A=∠B,所以2∠A+37°26′=180°,解得∠A=71°17′.
(3)因为∠A= ∠B= ∠C,所以设∠A=x,则
∠B=2x,∠C=3x,所以x+2x+3x=180°,解得x=30°,所以∠C=90°.
感悟新知
知1-练
3.
在△ABC中,∠A-∠C=35°,∠B-∠A=5°,求△ABC各内角的度数.
由已知,可得∠C=∠A-35°,∠B=∠A+5°.又因为∠A+∠B+∠C=180°,所以∠A+∠A+5°+∠A-35°=180°,即3∠A-30°=180°,解得∠A=70°.所以∠B=70°+5°=75°,∠C=70°-35°=35°.
解:
感悟新知
知1-练
4.
在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35° B.40°
C.45° D.50°
C
感悟新知
知1-练
5.
在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
D
感悟新知
知1-练
6.
在△ABC中,已知∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )
A.40° B.60°
C.80° D.90°
A
感悟新知
知1-练
7.
在△ABC中,∠A∶∠B∶∠C=3∶4∶5,则∠C等于( )
A.45° B.60°
C.75° D.90°
C
知识点
三角形的分类
知2-练
感悟新知
2
例2
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,试判断△ABC的形状,并说明理由.
引用辅助量x°,用x°表示出△ABC的三个
内角,在△ABC中,运用三角形内角和定理
构造方程,解方程后,求出△ABC中各角的
度数,再判断△ABC的形状.
导引:
感悟新知
知2-练
解:
△ABC是直角三角形.理由如下:
∵∠A∶∠B∶∠C=1∶2∶3,
∴可设∠A,∠B,∠C的度数分别为x°,2x°,3x°.在△ABC中,∠A+∠B+∠C=180°(三角形三个内角的和等于180°),
∴x+2x+3x=180,解得x=30.
∴∠C=3x°=90°,
∴△ABC是直角三角形.
知2-讲
总 结
感悟新知
判断一个三角形的形状的方法:(1)可以看三角形中最大的角的大小:最大角是锐角,三角形就是锐角三角形;最大角是直角,三角形就是直角三角形;最大角是钝角,三角形就是钝角三角形.(2)也可以通过角的比判断:两较小角的份数和小于最大角的份数,则此三角形为钝角三角形;两较小角的份数和等于最大角的份数(两锐角互余),则此三角形为直角三角形;两较小角的份数和大于最大角的份数,则此三角形为锐角三角形.
感悟新知
知2-练
1.
解:
在△ABC中,∠C=36°,∠A与∠B的比是1∶2,求∠A,∠B的度数.
因为∠A与∠B的比是1∶2,所以∠B=2∠A,
因为∠A+∠B+∠C=180°,∠C=36°,
所以∠A+2∠A+36°=180°,
解得∠A=48°,所以∠B=96°.
2.
感悟新知
知2-练
一个三角形三个内角的度数之比为2∶3∶7,求这个三角形的三个内角 的度数.
由题意可设这个三角形的三个内角的度数分别为2x,3x,7x,所以2x+3x+7x=180°,解得x=15°,所以2x=30°,3x=45°,7x=105°,所以这个三角形的三个内角的度数分别为30°,45°,105°.
解:
感悟新知
知2-练
例 3
如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向.
(1)试说明△ABC为直角三角形;
(2)求∠BCA的度数.
感悟新知
知2-练
(1)如图,过A作AF∥BD,∴∠BAF=∠ABD=40°.显然AF∥EC,∴∠CAF=∠ECA=50°.∴∠BAC=∠BAF+∠CAF=40°+50°=90°.∴△ABC为直角三角形.
(2)∵∠DBC=75°,∠DBA=40°,∴∠ABC=∠DBC-∠DBA=75°-40°=35°.∴在Rt△ABC中,∠BCA=90°-∠ABC=90°-35°=55°.
解:
知2-讲
总 结
感悟新知
本例主要考查建模思想,即把方位角建模成几何
图形中的角,同时应用了平行线的性质,三角形的内
角和及直角三角形的判定等.
1.
感悟新知
知2-练
解:
在△ABC中,∠C=42°,∠A=∠B,求∠B的度数.
因为∠C=42°,∠A=∠B,所以2∠B+42°=180°,解得∠B=69°.
2.
感悟新知
知2-练
求适合下列条件的△ABC的各内角的度数:
(1)∠A=∠B=30°;
(2)∠A=∠B=∠C;
(3)∠A=50°,∠A+∠B=∠C.
感悟新知
知2-练
在△ABC中,∠A+∠B+∠C=180°.
(1)因为∠A=∠B=30°,所以∠C=180°-30°-30°=120°.
(2)因为∠A=∠B=∠C,所以3∠A=3∠B=3∠C=180°,所以∠A=∠B=∠C=60°.
(3)因为∠A+∠B=∠C,所以2∠C=180°,∠C=90°.因为∠A=50°,所以∠B=180°-∠C-∠A=180°-90°-50°=40°.
解:
3.
感悟新知
知2-练
如图,在△ABC中,点D在AB上,点E在AC上,DE∥BC,若∠A=62°,∠AED=54°,则∠B的大小为( )
A.54° B.62°
C.64° D.74°
C
4.
感悟新知
知2-练
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
A.30° B.35°
C.40° D.50°
C
5.
感悟新知
知2-练
直角三角尺和直尺如图放置.若∠1=20°,则∠2的度数为( )
A.60° B.50°
C.40° D.30°
C
6.
感悟新知
知2-练
如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )
A.118° B.119°
C.120° D.121°
C
7.
感悟新知
知2-练
如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38°
C.48° D.88°
C
8.
感悟新知
知2-练
将一副三角尺如图放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边在同一条直线上,则∠1的度数为( )
A.75° B.65°
C.45° D.30°
C
课堂小结
三角形的内角和
知识总结
知识方法要点 关键总结 注意事项
三角形的内角和的定义 三角形的内角和等于180°. 注意单位度的符号是“°”
方法规律总结
(1)三角形是最常见的几何图形之一,在现实生活中有广泛的应用.学习时要注意多联系生活实际,学用结合. (2)在学习过程中,要注意知识之间的相互联系,尤其是前后知识间的因果关系,如借助平行线的性质推导出了三角形的内角和定理.
课堂小结
如图,说明∠A+∠B+∠C与∠ADC之间的关系.
易错点:非三角形问题用内角和定理而致错
三角形的内角和
课堂小结
解:
连接BD.∵∠A+∠ABD+∠ADB=180°,
∠C+∠DBC+∠CDB=180°,
∴∠A+∠ABD+∠ADB+∠C+∠DBC+∠CDB=360°,
又∵∠ADB+∠CDB+∠ADC=360°,
∴∠A+∠ABC+∠C+360°-∠ADC=360°,
∴∠A+∠ABC+∠C=∠ADC.
三角形的内角和
课堂小结
点拨:
连接BD,构成了△ABD和△BDC.本题易忽视四边形ABCD不是三角形,而错误地认为∠A+∠B+∠C=180°>∠ADC.
三角形的内角和
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
