冀教版数学七年级下9.3 三角形的角平分线、中线和高 课件(共53张PPT)
文档属性
| 名称 | 冀教版数学七年级下9.3 三角形的角平分线、中线和高 课件(共53张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 10:51:48 | ||
图片预览





文档简介
(共53张PPT)
9.3 三角形的角平分线、中线和高
第九章 二元一方程组
课时导入
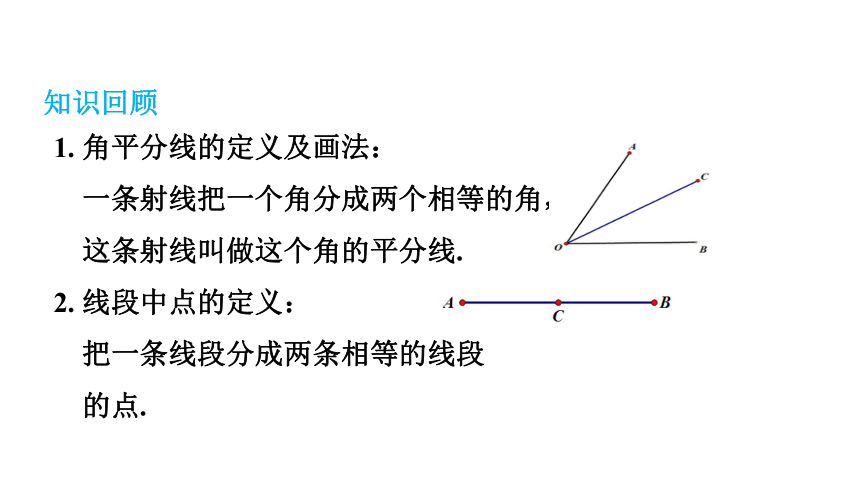
1. 角平分线的定义及画法:
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线.
2. 线段中点的定义:
把一条线段分成两条相等的线段
的点.
知识回顾
课时导入
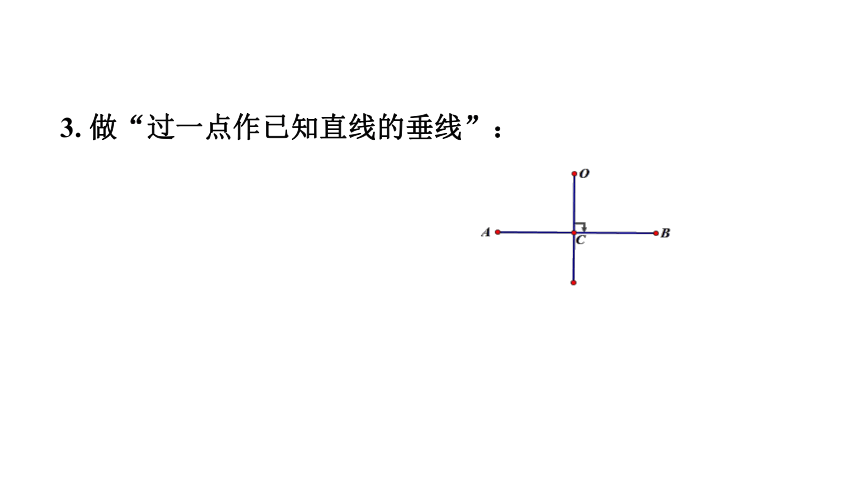
3. 做“过一点作已知直线的垂线”:
课时导入
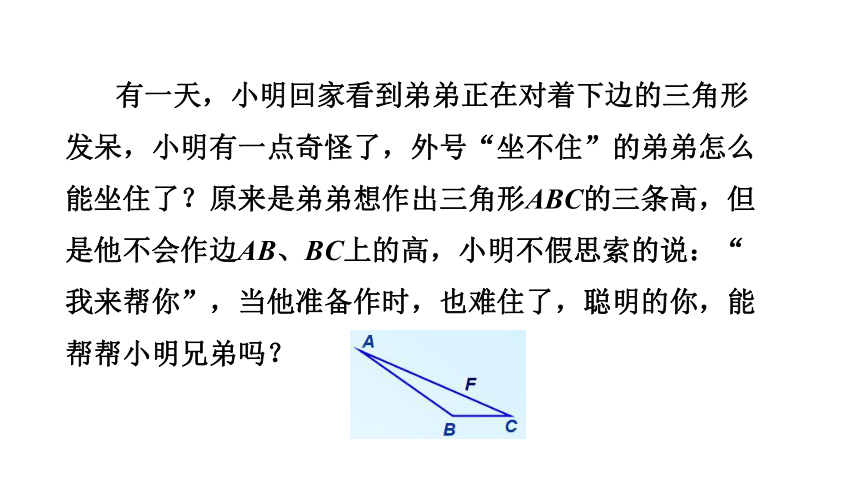
有一天,小明回家看到弟弟正在对着下边的三角形
发呆,小明有一点奇怪了,外号“坐不住”的弟弟怎么
能坐住了?原来是弟弟想作出三角形ABC的三条高,但
是他不会作边AB、BC上的高,小明不假思索的说:“
我来帮你”,当他准备作时,也难住了,聪明的你,能
帮帮小明兄弟吗?
知识点
三角形的角平分线
知1-讲
感悟新知
1
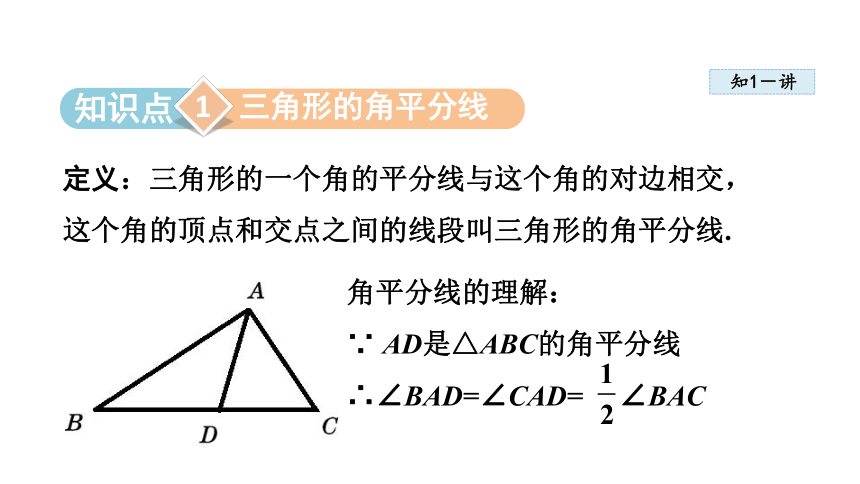
定义:三角形的一个角的平分线与这个角的对边相交,
这个角的顶点和交点之间的线段叫三角形的角平分线.
角平分线的理解:
∵ AD是△ABC的角平分线
∴∠BAD=∠CAD= ∠BAC
知1-讲
感悟新知
特别提醒
1.角的平分线是一条射线,而三角形的角平分线是一条线
段 .
2.三角形的角平分线是其内角的平分线的一部分 .故角的平
分线的性质三角形的角平分线都具有 .
知1-讲
感悟新知
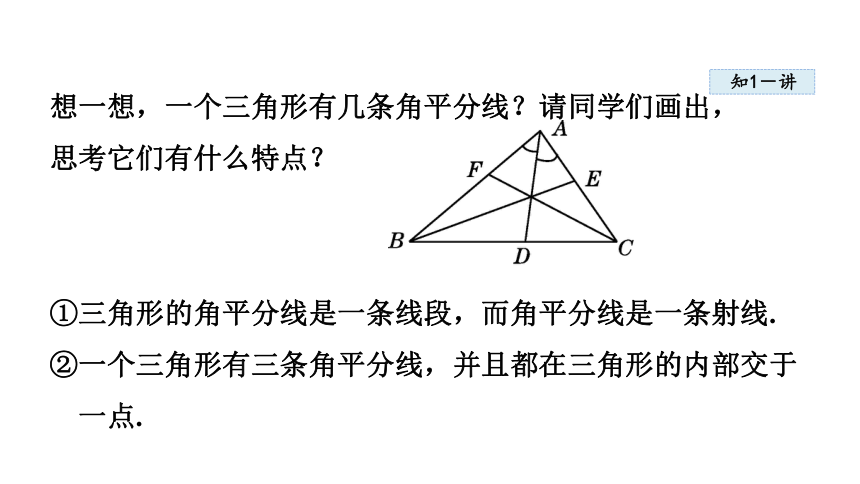
想一想,一个三角形有几条角平分线?请同学们画出,
思考它们有什么特点?
①三角形的角平分线是一条线段,而角平分线是一条射线.
②一个三角形有三条角平分线,并且都在三角形的内部交于
一点.
感悟新知
知1-练
例 1
导引:
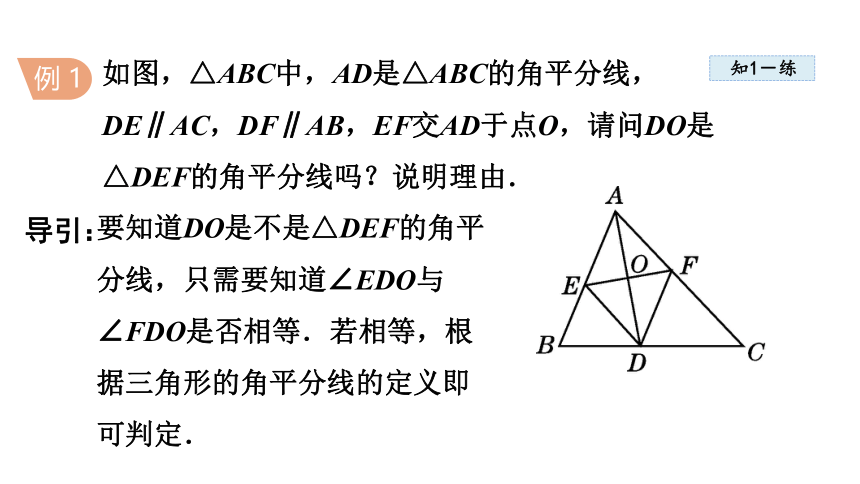
如图,△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?说明理由.
要知道DO是不是△DEF的角平
分线,只需要知道∠EDO与
∠FDO是否相等.若相等,根
据三角形的角平分线的定义即
可判定.
感悟新知
知1-练
DO是△DEF的角平分线.理由如下:
因为AD是△ABC的角平分线,
所以∠DAB=∠DAC(角平分线定义).
因为DE∥AC,DF∥AB,
所以∠DAC=∠ADE,∠DAB=∠ADF(两直线平行,内错角相等),所以∠ADE=∠ADF(等量代换),
所以DO是△DEF的角平分线.
解:
知1-讲
总 结
感悟新知
本例在解题过程中,先利用角平分线的定义,得
出相等的角,再结合相关条件(如平行等)推出新的一
组相等的角,最后由角平分线的定义说明角平分线,
它经历了定义→条件→定义的过程,这就是定义法.
感悟新知
知1-练
1.
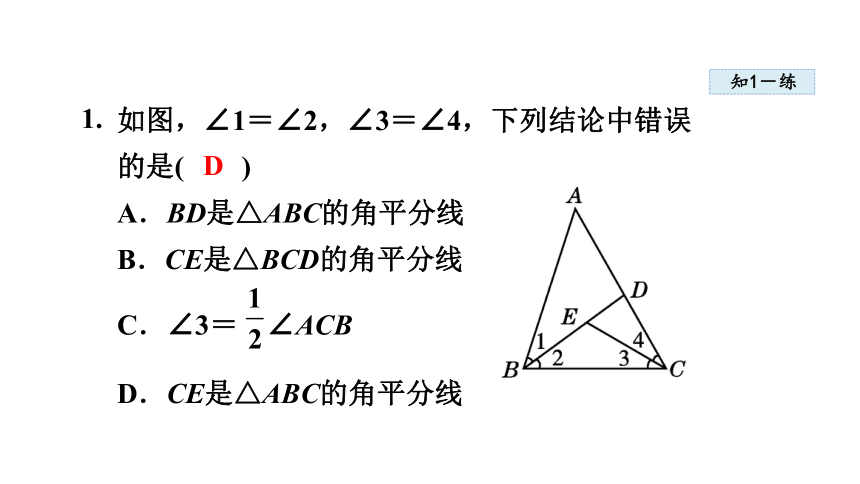
如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
D
感悟新知
知1-练
2.
一个三角形的三条角平分线的交点在( )
A.三角形内
B.三角形外
C.三角形的某边上
D.以上三种情形都有可能
A
知识点
三角形的中线
知2-讲
感悟新知
2
定义:在三角形中,连接一个顶点和它的对边中点
的线段叫做这个三角形的中线.
三角形中线的理解:
∵AD是△ ABC的中线
∴BD=CD= BC
知2-讲
感悟新知
特别解读
三角形的中线把三角形分成的两个三角形的面积和周长
的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差 .
知2-讲
感悟新知
想一想,一个三角形有几条中线?请同学们画出.
它们有什么特点?
①三角形的中线是一条线段.
②任何三角形有三条中线,并且都在三角形的内部交
于一点.
感悟新知
知2-练
例2
张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
根据等底同高的三角形的面积相
等,要等分三角形的面积,只需
要作出一条边上的中线即可.
导引:
感悟新知
知2-练
解:
根据要求,平分田地的直线必须经过三角形的顶点.画△ABC的中线AD(如图),则AD就把△ABC的面积平分成两份.这是因为AD是△ABC的中线,所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD中,因为BD,CD边上的高都是AE,所以由三角形的面积计算公式,知△ABD和△ACD的面积相等,
感悟新知
知2-练
因此,要把△ABC平分成两个三角形,只需画中线AD即可,这是一种平分方法.(本题答案不唯一,作AB,AC边上的中线也可以)
知2-讲
总 结
感悟新知
(1)三角形的任意一条中线都能把三角形分成面积相
等的两部分,即等底同高的三角形面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.
感悟新知
知2-练
1.
(1)如图,△ABC的面积等于10,AD是中线,分别求出△ABD和△ACD的面积.
(2)你能把一个三角形分成面积相等的两部分吗?分成面积相等的四部分呢?分成面积相等的三部分呢?
感悟新知
知2-练
解:
(1)因为AD是△ABC的中线,所以BD=DC= BC,所以S△ABD=S△ACD= S△ABC=5.
(2)①把一个三角形分成面积相等的两部分,如图所示,其中BD=DC= BC,S△ABD=S△ADC=
S△ABC.
(题①图)
感悟新知
知2-练
②把一个三角形分成面积相等的四部分,如图所示,其中BD=DE=EF=FC= BC,S△ABD=S△ADE=S△AEF=S△AFC= S△ABC.
(题②图)
感悟新知
知2-练
③把一个三角形分成面积相等的三部分,如图所示,其中BD=DE=EC= BC,S△ABD=S△ADE=S△AEC= S△ABC.
(题③图)
2.
感悟新知
知2-练
若AD是△ABC的中线,下列结论错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
3.
感悟新知
知2-练
已知D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
D
4.
感悟新知
知2-练
三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
B
5.
感悟新知
知2-练
如图,已知BD是△ABC的中线,AB=5,BC=3,则△ABD和△BCD的周长的差是( )
A.2 B.3
C.6 D.不能确定
A
6.
感悟新知
知2-练
如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1
C. D.
B
7.
感悟新知
知2-练
已知三角形的三条中线交于一点,则下列结论:
①这一点在三角形的内部;
②这一点有可能在三角形的外部;
③这一点是三角形的重心.
其中正确的结论有________.(填序号)
①③
知识点
三角形的高
知3-讲
感悟新知
3
定义:从三角形一个顶点向它的对边所在的直线做垂
线,顶点和垂足间的线段叫做三角形的高线,简称三
角形的高.
对三角形高的理解:
∵AD是△ ABC的高
∴AD⊥BC或∠ADC=∠ADB =90°
知3-讲
感悟新知
想一想,一个三角形有几条高?请同学们用同样的方
法画出.它们有什么特点?
知3-讲
感悟新知
①三角形的高是一条线段.
②一个三角形有三条高,三条高(或高的延长线)相交
于一点.可分为锐角三角形(内部),直角三角形(直角
顶点),钝角三角形(外部).
感悟新知
知3-练
例 3
(动手操作题,易错题)画出图中△ABC的三条高.(要标明字母,不写画法)
感悟新知
知3-练
导引:
“作一边上的高”,即可看作“过一点(这边所对
角的顶点)作已知直线(这边所在的直线)的垂线.”
按照“过一点作已知直线的垂线”进行作图,顶
点与垂足之间的线段即为该边上的高;需注意AB,
BC边上的高在三角形的外部,作高时先延长AB
与CB.
感悟新知
知3-练
解:
如图所示.
知3-讲
总 结
感悟新知
(1)作三角形的高时,找准顶点和对边是关键,作高
的步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、二
找(移动三角尺使另一条直角
边通过要作高的顶点)、三画
线(画垂线段),如图.
知3-讲
总 结
感悟新知
(2)注意:高是线段,垂线是直线.
1.
感悟新知
知3-练
如图.AD,AE,AF分别是△ABC的中线、角平分线和高.请你指出图中相等的角及相等的线段.
相等的角有∠BAE=∠EAC,∠AFB=∠AFC;相等的线段有BD=DC.
解:
2.
感悟新知
知3-练
解:
分别画出锐角三角形、直角三角形和钝角三角形的三条角平分线、三条中线和三条高.
(1)锐角三角形(如图所示).
(2)直角三角形(如图所示).
感悟新知
知3-练
(3)钝角三角形(如图所示).
3.
感悟新知
知3-练
如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°.
求∠DAE的度数.
感悟新知
知3-练
解:
因为AD平分∠BAC,所以∠CAD=
∠BAC=20°.因为∠ADE是△ACD的一个外角,所以∠ADE=∠C+∠CAD=60°+20°=80°.又因为AE是△ABC的高,所以∠AED=90°,所以在△AED中,∠DAE=180°-∠AED-∠ADE=180°-90°-80°=10°.
4.
感悟新知
知3-练
如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE交于点O.求∠BOC的度数.
感悟新知
知3-练
解:
因为BD是△ABC的角平分线,
所以∠OBC= ∠ABC=31°.因为CE是△ABC的高,所以∠BEC=90°,所以在△BEC中,∠ECB=180°-∠EBC-∠BEC=180°-62°-90°=28°,所以在△BOC中,∠BOC=180°-∠OBC-∠OCB=180°-31°-28°=121°.
5.
感悟新知
知3-练
如图,在△ABC中,AD是高,BE是角平分线,AD,BE交于点F,∠C= 30°,
∠BFD=70°.求∠BAC的度数.
感悟新知
知3-练
解:
因为AD是△ABC的高,
所以∠ADB=90°,所以在△BFD中,∠FBD=180°-∠FDB-∠BFD=180°-90°-70°=20°.又因为BE是△ABC的角平分线,所以∠ABF=∠FBD=20°,所以∠ABC=40°,所以∠BAC=180°-∠ABC-∠C=180°-40°-30°=110°.
6.
感悟新知
知3-练
下列图形中,AD是△ABC的高的是( )
B
7.
感悟新知
知3-练
下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
8.
感悟新知
知3-练
如图,已知在直角三角形ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B,C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
A.不变
B.增大
C.减小
D.先变大再变小
C
9.
感悟新知
知3-练
能把三角形平分成两个面积相等的三角形的线段是( )
A.三角形的中线
B.三角形的高
C.三角形的角平分线
D.以上三种情况都正确
A
课堂小结
三角形的角平分
线、中线和高
1.三角形的中线
(1)定义:三角形的中线是一条线段.
(2)三角形的三条中线相交于一点,这一点叫做三
角形的重心.
课堂小结
三角形的角平分
线、中线和高
2.三角形的角平分线
(1)定义:三角形的角平分线是一条线段.
(2)三角形三条角平分线相交于一点,这一点叫做
三角形的内心.
课堂小结
三角形的角平分
线、中线和高
3. 三角形的高
定义:从三角形一个顶点向它的对边所在的直线
做垂线,顶点和垂足间的线段叫做三角形的高线,
简称三角形的高.
9.3 三角形的角平分线、中线和高
第九章 二元一方程组
课时导入
1. 角平分线的定义及画法:
一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线.
2. 线段中点的定义:
把一条线段分成两条相等的线段
的点.
知识回顾
课时导入
3. 做“过一点作已知直线的垂线”:
课时导入
有一天,小明回家看到弟弟正在对着下边的三角形
发呆,小明有一点奇怪了,外号“坐不住”的弟弟怎么
能坐住了?原来是弟弟想作出三角形ABC的三条高,但
是他不会作边AB、BC上的高,小明不假思索的说:“
我来帮你”,当他准备作时,也难住了,聪明的你,能
帮帮小明兄弟吗?
知识点
三角形的角平分线
知1-讲
感悟新知
1
定义:三角形的一个角的平分线与这个角的对边相交,
这个角的顶点和交点之间的线段叫三角形的角平分线.
角平分线的理解:
∵ AD是△ABC的角平分线
∴∠BAD=∠CAD= ∠BAC
知1-讲
感悟新知
特别提醒
1.角的平分线是一条射线,而三角形的角平分线是一条线
段 .
2.三角形的角平分线是其内角的平分线的一部分 .故角的平
分线的性质三角形的角平分线都具有 .
知1-讲
感悟新知
想一想,一个三角形有几条角平分线?请同学们画出,
思考它们有什么特点?
①三角形的角平分线是一条线段,而角平分线是一条射线.
②一个三角形有三条角平分线,并且都在三角形的内部交于
一点.
感悟新知
知1-练
例 1
导引:
如图,△ABC中,AD是△ABC的角平分线,DE∥AC,DF∥AB,EF交AD于点O,请问DO是△DEF的角平分线吗?说明理由.
要知道DO是不是△DEF的角平
分线,只需要知道∠EDO与
∠FDO是否相等.若相等,根
据三角形的角平分线的定义即
可判定.
感悟新知
知1-练
DO是△DEF的角平分线.理由如下:
因为AD是△ABC的角平分线,
所以∠DAB=∠DAC(角平分线定义).
因为DE∥AC,DF∥AB,
所以∠DAC=∠ADE,∠DAB=∠ADF(两直线平行,内错角相等),所以∠ADE=∠ADF(等量代换),
所以DO是△DEF的角平分线.
解:
知1-讲
总 结
感悟新知
本例在解题过程中,先利用角平分线的定义,得
出相等的角,再结合相关条件(如平行等)推出新的一
组相等的角,最后由角平分线的定义说明角平分线,
它经历了定义→条件→定义的过程,这就是定义法.
感悟新知
知1-练
1.
如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
D
感悟新知
知1-练
2.
一个三角形的三条角平分线的交点在( )
A.三角形内
B.三角形外
C.三角形的某边上
D.以上三种情形都有可能
A
知识点
三角形的中线
知2-讲
感悟新知
2
定义:在三角形中,连接一个顶点和它的对边中点
的线段叫做这个三角形的中线.
三角形中线的理解:
∵AD是△ ABC的中线
∴BD=CD= BC
知2-讲
感悟新知
特别解读
三角形的中线把三角形分成的两个三角形的面积和周长
的关系:
1. 两个三角形的面积相等;
2. 两个三角形的周长的差等于这两个三角形另两边的差 .
知2-讲
感悟新知
想一想,一个三角形有几条中线?请同学们画出.
它们有什么特点?
①三角形的中线是一条线段.
②任何三角形有三条中线,并且都在三角形的内部交
于一点.
感悟新知
知2-练
例2
张大爷的两个儿子都长大成人了,也该分家了.于是张大爷准备把如图所示的一块三角形田地平均分给两个儿子,两个儿子要求分成的两块田地的形状仍然是三角形,请你帮助张大爷提出一种平分的方案.
根据等底同高的三角形的面积相
等,要等分三角形的面积,只需
要作出一条边上的中线即可.
导引:
感悟新知
知2-练
解:
根据要求,平分田地的直线必须经过三角形的顶点.画△ABC的中线AD(如图),则AD就把△ABC的面积平分成两份.这是因为AD是△ABC的中线,所以BD=DC.过点A作AE⊥BC于点E.在△ABD和△ACD中,因为BD,CD边上的高都是AE,所以由三角形的面积计算公式,知△ABD和△ACD的面积相等,
感悟新知
知2-练
因此,要把△ABC平分成两个三角形,只需画中线AD即可,这是一种平分方法.(本题答案不唯一,作AB,AC边上的中线也可以)
知2-讲
总 结
感悟新知
(1)三角形的任意一条中线都能把三角形分成面积相
等的两部分,即等底同高的三角形面积相等;
(2)拓展:在两个三角形中:底、高、面积这三个量,
如果有其中的两个量相等,那么第三个量也相等.
感悟新知
知2-练
1.
(1)如图,△ABC的面积等于10,AD是中线,分别求出△ABD和△ACD的面积.
(2)你能把一个三角形分成面积相等的两部分吗?分成面积相等的四部分呢?分成面积相等的三部分呢?
感悟新知
知2-练
解:
(1)因为AD是△ABC的中线,所以BD=DC= BC,所以S△ABD=S△ACD= S△ABC=5.
(2)①把一个三角形分成面积相等的两部分,如图所示,其中BD=DC= BC,S△ABD=S△ADC=
S△ABC.
(题①图)
感悟新知
知2-练
②把一个三角形分成面积相等的四部分,如图所示,其中BD=DE=EF=FC= BC,S△ABD=S△ADE=S△AEF=S△AFC= S△ABC.
(题②图)
感悟新知
知2-练
③把一个三角形分成面积相等的三部分,如图所示,其中BD=DE=EC= BC,S△ABD=S△ADE=S△AEC= S△ABC.
(题③图)
2.
感悟新知
知2-练
若AD是△ABC的中线,下列结论错误的是( )
A.AB=BC B.BD=DC
C.AD平分BC D.BC=2DC
A
3.
感悟新知
知2-练
已知D,E分别是△ABC的边AC,BC的中点,那么下列说法中不正确的是( )
A.DE是△BCD的中线
B.BD是△ABC的中线
C.AD=DC,BE=EC
D.AD=EC,DC=BE
D
4.
感悟新知
知2-练
三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
B
5.
感悟新知
知2-练
如图,已知BD是△ABC的中线,AB=5,BC=3,则△ABD和△BCD的周长的差是( )
A.2 B.3
C.6 D.不能确定
A
6.
感悟新知
知2-练
如图,在△ABC中,D,E分别为BC,AD的中点,且S△ABC=4,则S阴影为( )
A.2 B.1
C. D.
B
7.
感悟新知
知2-练
已知三角形的三条中线交于一点,则下列结论:
①这一点在三角形的内部;
②这一点有可能在三角形的外部;
③这一点是三角形的重心.
其中正确的结论有________.(填序号)
①③
知识点
三角形的高
知3-讲
感悟新知
3
定义:从三角形一个顶点向它的对边所在的直线做垂
线,顶点和垂足间的线段叫做三角形的高线,简称三
角形的高.
对三角形高的理解:
∵AD是△ ABC的高
∴AD⊥BC或∠ADC=∠ADB =90°
知3-讲
感悟新知
想一想,一个三角形有几条高?请同学们用同样的方
法画出.它们有什么特点?
知3-讲
感悟新知
①三角形的高是一条线段.
②一个三角形有三条高,三条高(或高的延长线)相交
于一点.可分为锐角三角形(内部),直角三角形(直角
顶点),钝角三角形(外部).
感悟新知
知3-练
例 3
(动手操作题,易错题)画出图中△ABC的三条高.(要标明字母,不写画法)
感悟新知
知3-练
导引:
“作一边上的高”,即可看作“过一点(这边所对
角的顶点)作已知直线(这边所在的直线)的垂线.”
按照“过一点作已知直线的垂线”进行作图,顶
点与垂足之间的线段即为该边上的高;需注意AB,
BC边上的高在三角形的外部,作高时先延长AB
与CB.
感悟新知
知3-练
解:
如图所示.
知3-讲
总 结
感悟新知
(1)作三角形的高时,找准顶点和对边是关键,作高
的步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、二
找(移动三角尺使另一条直角
边通过要作高的顶点)、三画
线(画垂线段),如图.
知3-讲
总 结
感悟新知
(2)注意:高是线段,垂线是直线.
1.
感悟新知
知3-练
如图.AD,AE,AF分别是△ABC的中线、角平分线和高.请你指出图中相等的角及相等的线段.
相等的角有∠BAE=∠EAC,∠AFB=∠AFC;相等的线段有BD=DC.
解:
2.
感悟新知
知3-练
解:
分别画出锐角三角形、直角三角形和钝角三角形的三条角平分线、三条中线和三条高.
(1)锐角三角形(如图所示).
(2)直角三角形(如图所示).
感悟新知
知3-练
(3)钝角三角形(如图所示).
3.
感悟新知
知3-练
如图,在△ABC中,AD是角平分线,AE是高,∠BAC=40°,∠C=60°.
求∠DAE的度数.
感悟新知
知3-练
解:
因为AD平分∠BAC,所以∠CAD=
∠BAC=20°.因为∠ADE是△ACD的一个外角,所以∠ADE=∠C+∠CAD=60°+20°=80°.又因为AE是△ABC的高,所以∠AED=90°,所以在△AED中,∠DAE=180°-∠AED-∠ADE=180°-90°-80°=10°.
4.
感悟新知
知3-练
如图,在△ABC中,∠ABC=62°,BD是角平分线,CE是高,BD与CE交于点O.求∠BOC的度数.
感悟新知
知3-练
解:
因为BD是△ABC的角平分线,
所以∠OBC= ∠ABC=31°.因为CE是△ABC的高,所以∠BEC=90°,所以在△BEC中,∠ECB=180°-∠EBC-∠BEC=180°-62°-90°=28°,所以在△BOC中,∠BOC=180°-∠OBC-∠OCB=180°-31°-28°=121°.
5.
感悟新知
知3-练
如图,在△ABC中,AD是高,BE是角平分线,AD,BE交于点F,∠C= 30°,
∠BFD=70°.求∠BAC的度数.
感悟新知
知3-练
解:
因为AD是△ABC的高,
所以∠ADB=90°,所以在△BFD中,∠FBD=180°-∠FDB-∠BFD=180°-90°-70°=20°.又因为BE是△ABC的角平分线,所以∠ABF=∠FBD=20°,所以∠ABC=40°,所以∠BAC=180°-∠ABC-∠C=180°-40°-30°=110°.
6.
感悟新知
知3-练
下列图形中,AD是△ABC的高的是( )
B
7.
感悟新知
知3-练
下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
8.
感悟新知
知3-练
如图,已知在直角三角形ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B,C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
A.不变
B.增大
C.减小
D.先变大再变小
C
9.
感悟新知
知3-练
能把三角形平分成两个面积相等的三角形的线段是( )
A.三角形的中线
B.三角形的高
C.三角形的角平分线
D.以上三种情况都正确
A
课堂小结
三角形的角平分
线、中线和高
1.三角形的中线
(1)定义:三角形的中线是一条线段.
(2)三角形的三条中线相交于一点,这一点叫做三
角形的重心.
课堂小结
三角形的角平分
线、中线和高
2.三角形的角平分线
(1)定义:三角形的角平分线是一条线段.
(2)三角形三条角平分线相交于一点,这一点叫做
三角形的内心.
课堂小结
三角形的角平分
线、中线和高
3. 三角形的高
定义:从三角形一个顶点向它的对边所在的直线
做垂线,顶点和垂足间的线段叫做三角形的高线,
简称三角形的高.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
