广东省连州市连州中学高一数学《4.2.1函数模型及其应用》课件
文档属性
| 名称 | 广东省连州市连州中学高一数学《4.2.1函数模型及其应用》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 00:00:00 | ||
图片预览






文档简介
课件19张PPT。 函数模型及其应用①了解指数函数、对数函数以及幂函数的增
长特征,知道直线上升、指数增长、对数增
长等不同函数类型增长的含义。
②了解函数模型(如指数函数、对数函数、
幂函数、分段函数等在社会生活中普遍使用
的函数模型)的广泛应用。考试要求:知识要点一.几类不同增长速度的函数模型?
在区间(0,+∞)上,尽管函数y=ax(a>1),?
y=logax(a>1)和y=xn(n>0)都是增函数,但它们的增长
速度不同,而且不在同一个“档次”上.随着x的增
大,y=ax(a>1)的增长速度越来越快,会超过并远远
大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速
度则会越来越慢.因此,总会存在一个x0,当x>x0时,
就有logax1.思维过程实际问题 函数模型
实际问题的解 函数模型的解抽象概括还原说明推理演算2.解题程序?
(1)读:阅读理解文字表达的题意,分清条件和结论, 理顺数量关系,这一关是基础.?
(2)建:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型.熟悉基本数学模型,正确进行建“模”是解题的关键.?
(3)解:求解数学模型,得到数学结论.注意各变量的实际意义.?
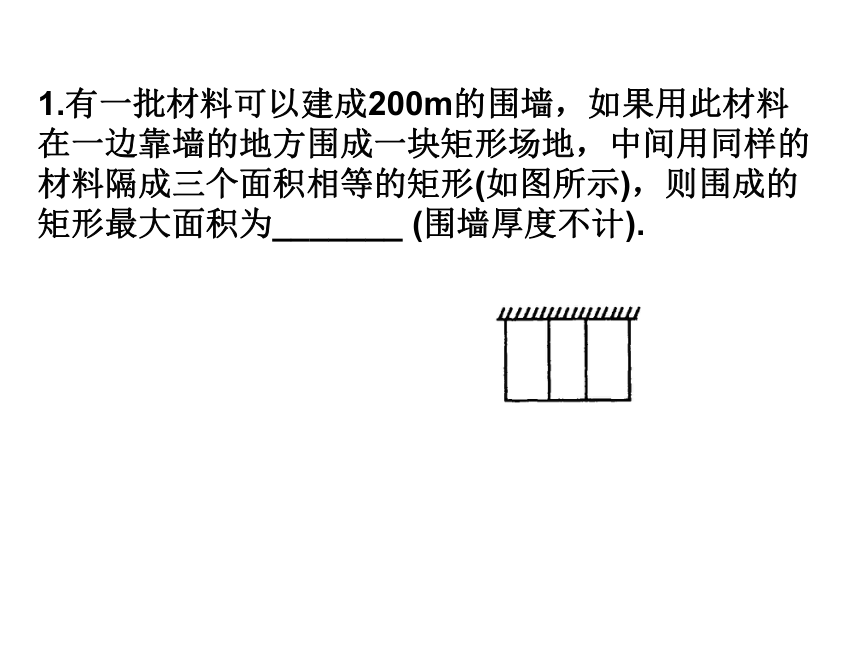
(5)答:将数学结论还原给实际问题的结果.1.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的
矩形最大面积为_______ (围墙厚度不计). 1. 某商场出售甲、乙两种不同价格的电脑,其中甲电脑供不应求,连续两次提价10%,而乙电脑由于外观原因连续两次降价10%,最后甲乙两台电脑均以9801元售出,若商场同时售出甲乙两台电脑各一台,与价格不升不降比较,商场盈利的情况是( )?
A.前后相同? B.少赚598元?
C.多赚980.1元 D.多赚498.5元B?题型分析题型1.营销问题1.某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是( )题型2.行程问题2.某人开汽车以60km/h的速率从A地到150km远处的B地,在B地停留1h后,再以50km/h的速度返回A地.把汽车与A地的距离xkm表示为时间th(从A地出发开始)的函数.
1. 资料表明:某电脑公司生产A种型号的家庭电脑,1995年平均每台电脑生产成本为5000元,并以纯利润20%标定出厂价(1996年初生产成本与1995年相同).1996年开始,公司更新设备,大力推进技术创新,并加强企业内部管理,从而生产成本逐年降低,2000年平均每台A种型号的家庭电脑尽管出厂价仅为1996年出厂价的60%,但却实现了纯利润50%的高收益,求?(1)2000年每台电脑的生产成本;?
(2)以1995年生产成本的基数,1995年至2000年生产成本平均每年降低的百分数(精确到0.01).?[点评] 有关增长率(或降低率)问题,其函数模型应是指数函数模型.题型3.增长率问题2.(07年上海卷)近年来,太阳能技术运用的步伐日益加快,2002年全球太阳电池的年生产量达到670兆瓦,年生产量的增长率为34%,以后四年中,年生产量的增长率逐年递增2%(如:2003年的年生产量的增长率为36%).?
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)???[点评](1)关键是利用已知函数模型,来建立新的利润函数模型.(2)函数的最大值问题,解法较多,其中求导法是一个较好的方法.题型4.决策问题2.(07年福建卷)某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;?
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a)?3. 某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102kg)与上市时间t(单位:天)的数据如下表:
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系:?
①Q=at+b;②Q=at2+bt+c;③Q=a·bt;?
④Q=a·logbt.?
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.[点评]本题是从若干函数模型中选择某一模型来刻划一些数据的变化规律,关键在于分析各模型的变化情况与实际数据的变化情况是否吻合.小结:
在引入自变量建立目标函数解决实际问题时,一是要注意自变量的取值范围,二是要检验结果,看是否符合实际问题要求. 问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位) 3.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台.已知生产家电产品每台所需工时和每台产值如下表:【解题回顾】解答本题的思路是:列出关于x、y、z的两个等式(①和②),将y和z用x表示后代入s,使s成为x的一次函数s=-x+1080,讨论s在x≥30条件下的最大值. 【解题回顾】看似繁杂的文字题,其背景不过是两个一次函数,当然因x∈N*,故实际上是两个等差数列. 4.一家庭(父亲、母亲、孩子)去某地旅游,有两个旅行社同时发出邀请,且有各自的优惠政策,甲旅行社承诺:如果父亲买一张全票,则其家庭成员(母亲与孩子,不论孩子多少与大)均可享受半价;乙旅行社承诺:家庭旅行算团体票,按原价的2/3计算,这两家旅行社的原价是一样的,若家庭中孩子数不同(至少一个),试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪一家旅行社更优惠?
长特征,知道直线上升、指数增长、对数增
长等不同函数类型增长的含义。
②了解函数模型(如指数函数、对数函数、
幂函数、分段函数等在社会生活中普遍使用
的函数模型)的广泛应用。考试要求:知识要点一.几类不同增长速度的函数模型?
在区间(0,+∞)上,尽管函数y=ax(a>1),?
y=logax(a>1)和y=xn(n>0)都是增函数,但它们的增长
速度不同,而且不在同一个“档次”上.随着x的增
大,y=ax(a>1)的增长速度越来越快,会超过并远远
大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速
度则会越来越慢.因此,总会存在一个x0,当x>x0时,
就有logax
实际问题的解 函数模型的解抽象概括还原说明推理演算2.解题程序?
(1)读:阅读理解文字表达的题意,分清条件和结论, 理顺数量关系,这一关是基础.?
(2)建:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型.熟悉基本数学模型,正确进行建“模”是解题的关键.?
(3)解:求解数学模型,得到数学结论.注意各变量的实际意义.?
(5)答:将数学结论还原给实际问题的结果.1.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图所示),则围成的
矩形最大面积为_______ (围墙厚度不计). 1. 某商场出售甲、乙两种不同价格的电脑,其中甲电脑供不应求,连续两次提价10%,而乙电脑由于外观原因连续两次降价10%,最后甲乙两台电脑均以9801元售出,若商场同时售出甲乙两台电脑各一台,与价格不升不降比较,商场盈利的情况是( )?
A.前后相同? B.少赚598元?
C.多赚980.1元 D.多赚498.5元B?题型分析题型1.营销问题1.某学生离家去学校,为了锻炼身体,一开始跑步前进,跑累了再走余下的路程,下图中,纵轴表示离学校的距离,横轴表示出发后的时间,则下列四个图形中较符合该学生的走法的是( )题型2.行程问题2.某人开汽车以60km/h的速率从A地到150km远处的B地,在B地停留1h后,再以50km/h的速度返回A地.把汽车与A地的距离xkm表示为时间th(从A地出发开始)的函数.
1. 资料表明:某电脑公司生产A种型号的家庭电脑,1995年平均每台电脑生产成本为5000元,并以纯利润20%标定出厂价(1996年初生产成本与1995年相同).1996年开始,公司更新设备,大力推进技术创新,并加强企业内部管理,从而生产成本逐年降低,2000年平均每台A种型号的家庭电脑尽管出厂价仅为1996年出厂价的60%,但却实现了纯利润50%的高收益,求?(1)2000年每台电脑的生产成本;?
(2)以1995年生产成本的基数,1995年至2000年生产成本平均每年降低的百分数(精确到0.01).?[点评] 有关增长率(或降低率)问题,其函数模型应是指数函数模型.题型3.增长率问题2.(07年上海卷)近年来,太阳能技术运用的步伐日益加快,2002年全球太阳电池的年生产量达到670兆瓦,年生产量的增长率为34%,以后四年中,年生产量的增长率逐年递增2%(如:2003年的年生产量的增长率为36%).?
(1)求2006年全球太阳电池的年生产量(结果精确到0.1兆瓦);
(2)目前太阳电池产业存在的主要问题是市场安装量远小于生产量,2006年的实际安装量为1420兆瓦.假设以后若干年内太阳电池的年生产量的增长率保持在42%,到2010年,要使年安装量与年生产量基本持平(即年安装量不少于年生产量的95%),这四年中太阳电池的年安装量的平均增长率至少应达到多少(结果精确到0.1%)???[点评](1)关键是利用已知函数模型,来建立新的利润函数模型.(2)函数的最大值问题,解法较多,其中求导法是一个较好的方法.题型4.决策问题2.(07年福建卷)某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交a元(3≤a≤5)的管理费,预计当每件产品的售价为x元(9≤x≤11)时,一年的销售量为(12-x)2万件.(1)求分公司一年的利润L(万元)与每件产品的售价x的函数关系式;?
(2)当每件产品的售价为多少元时,分公司一年的利润L最大,并求出L的最大值Q(a)?3. 某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102kg)与上市时间t(单位:天)的数据如下表:
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系:?
①Q=at+b;②Q=at2+bt+c;③Q=a·bt;?
④Q=a·logbt.?
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.[点评]本题是从若干函数模型中选择某一模型来刻划一些数据的变化规律,关键在于分析各模型的变化情况与实际数据的变化情况是否吻合.小结:
在引入自变量建立目标函数解决实际问题时,一是要注意自变量的取值范围,二是要检验结果,看是否符合实际问题要求. 问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位) 3.某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台.已知生产家电产品每台所需工时和每台产值如下表:【解题回顾】解答本题的思路是:列出关于x、y、z的两个等式(①和②),将y和z用x表示后代入s,使s成为x的一次函数s=-x+1080,讨论s在x≥30条件下的最大值. 【解题回顾】看似繁杂的文字题,其背景不过是两个一次函数,当然因x∈N*,故实际上是两个等差数列. 4.一家庭(父亲、母亲、孩子)去某地旅游,有两个旅行社同时发出邀请,且有各自的优惠政策,甲旅行社承诺:如果父亲买一张全票,则其家庭成员(母亲与孩子,不论孩子多少与大)均可享受半价;乙旅行社承诺:家庭旅行算团体票,按原价的2/3计算,这两家旅行社的原价是一样的,若家庭中孩子数不同(至少一个),试分别列出两家旅行社优惠政策实施后的孩子个数为变量的收费表达式,比较选择哪一家旅行社更优惠?
