广东省连州市连州中学高一数学《对数函数》课件
文档属性
| 名称 | 广东省连州市连州中学高一数学《对数函数》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 97.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 19:35:42 | ||
图片预览








文档简介
课件25张PPT。对数与对数函数考试要求:?
① 理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
② 理解对数函数的概念,理解对数函数的单调性,掌握函数图像通过的特殊点。
③ 知道对数函数是一类重要的函数模型。
④了解指数函数y=ax与对数函数y=logax互为反函数
(a>0,a≠1). 如果a(a>0,a≠1)的x次幂等于N,即ax=N,那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数,式子logaN叫做对数式.
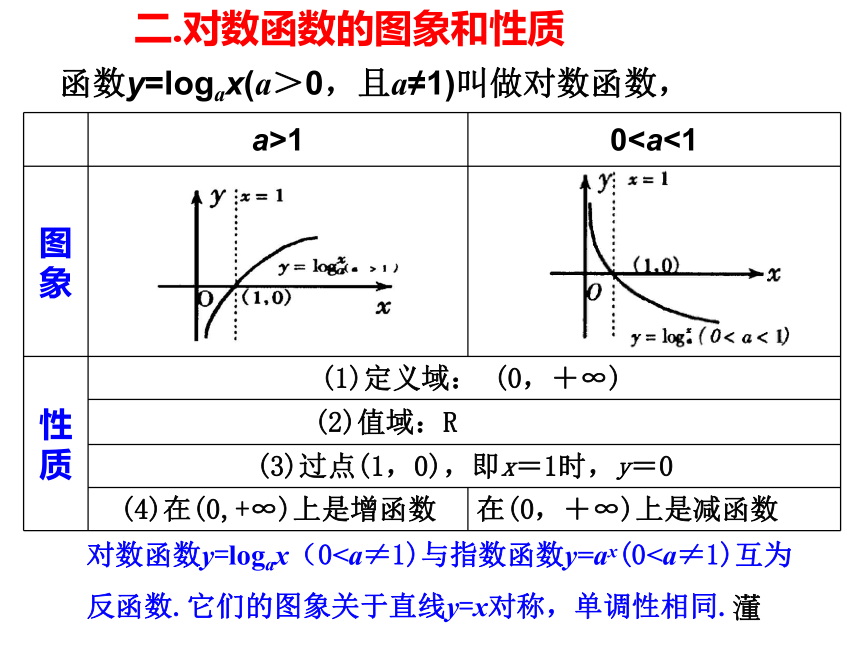
常用对数:lgN 自然对数:lnN(1)对数的定义一、对数与对数运算如果a>0,a≠1,M>0,N>0,那么 (3)对数的运算性质(2)(4)换底公式 题型1.对数式的运算注意对数运算性质的正用和逆用A练习2二.对数函数的图象和性质函数y=logax(a>0,且a≠1)叫做对数函数,对数函数y=logax(0反函数.它们的图象关于直线y=x对称,单调性相同.?题型2.比较大小 练习:比较大小,并说明理由.方法:作直线y=1
结论:看x轴上方的图象,底数
越大,越远离y轴正半轴.题型3.对数函数的图象与性质的应用1.如右图,三个对数函数的图象,若ax1=bx2=cx3>1,则x1,x2,x3的大小关系是( )
A.x1>x2>x3
B.x3>x2>x1
C.x3>x1>x2
D.x2>x1>x3A练习:2.(2010·全国Ⅰ)已知函数f(x)=|lgx|.若a≠b,且f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞) B.[1,+∞)
C.(2,+∞) D.[2,+∞)C3.设0A.(-∞,0) B.(0,+∞)
C.(-∞,loga3) D.(loga3,+∞)C题型4. 对数函数的综合问题[例1]练习1:[例2] 若函数f(x)=logax(a>0且a≠1)在区间[a,2a]上的最大值与最小值之比是3∶1,求a的值.[点评] 对数函数的最值问题,一般要考察单调性;由于底数a的范围是a>0且a≠1,所以必须分类讨论.练习2.设函数f(x)=ax+loga(x+1)(a>0且a≠1)在[0,1]上的最大值与最小值之和为a,求a的值.巩固练习例3练习2反函数1.对数函数y=logax(a>0, a≠1)与指数函数y=ax(a>0, a≠1) 互为反函数. ?2.反函数的定义域和值域分别是原函数的值域和定义域。所以,反函数的定义域不能由其解析式来求,而应该是原函数的值域。3.互为反函数的两个函数具有相同的单调性,它们的图象关于直线y=x对称。主要题型: 反函数性质的应用2
① 理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
② 理解对数函数的概念,理解对数函数的单调性,掌握函数图像通过的特殊点。
③ 知道对数函数是一类重要的函数模型。
④了解指数函数y=ax与对数函数y=logax互为反函数
(a>0,a≠1). 如果a(a>0,a≠1)的x次幂等于N,即ax=N,那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数,式子logaN叫做对数式.
常用对数:lgN 自然对数:lnN(1)对数的定义一、对数与对数运算如果a>0,a≠1,M>0,N>0,那么 (3)对数的运算性质(2)(4)换底公式 题型1.对数式的运算注意对数运算性质的正用和逆用A练习2二.对数函数的图象和性质函数y=logax(a>0,且a≠1)叫做对数函数,对数函数y=logax(0
结论:看x轴上方的图象,底数
越大,越远离y轴正半轴.题型3.对数函数的图象与性质的应用1.如右图,三个对数函数的图象,若ax1=bx2=cx3>1,则x1,x2,x3的大小关系是( )
A.x1>x2>x3
B.x3>x2>x1
C.x3>x1>x2
D.x2>x1>x3A练习:2.(2010·全国Ⅰ)已知函数f(x)=|lgx|.若a≠b,且f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞) B.[1,+∞)
C.(2,+∞) D.[2,+∞)C3.设0
C.(-∞,loga3) D.(loga3,+∞)C题型4. 对数函数的综合问题[例1]练习1:[例2] 若函数f(x)=logax(a>0且a≠1)在区间[a,2a]上的最大值与最小值之比是3∶1,求a的值.[点评] 对数函数的最值问题,一般要考察单调性;由于底数a的范围是a>0且a≠1,所以必须分类讨论.练习2.设函数f(x)=ax+loga(x+1)(a>0且a≠1)在[0,1]上的最大值与最小值之和为a,求a的值.巩固练习例3练习2反函数1.对数函数y=logax(a>0, a≠1)与指数函数y=ax(a>0, a≠1) 互为反函数. ?2.反函数的定义域和值域分别是原函数的值域和定义域。所以,反函数的定义域不能由其解析式来求,而应该是原函数的值域。3.互为反函数的两个函数具有相同的单调性,它们的图象关于直线y=x对称。主要题型: 反函数性质的应用2
