广东省连州市连州中学高一数学《三角恒等变换》课件
文档属性
| 名称 | 广东省连州市连州中学高一数学《三角恒等变换》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 00:00:00 | ||
图片预览





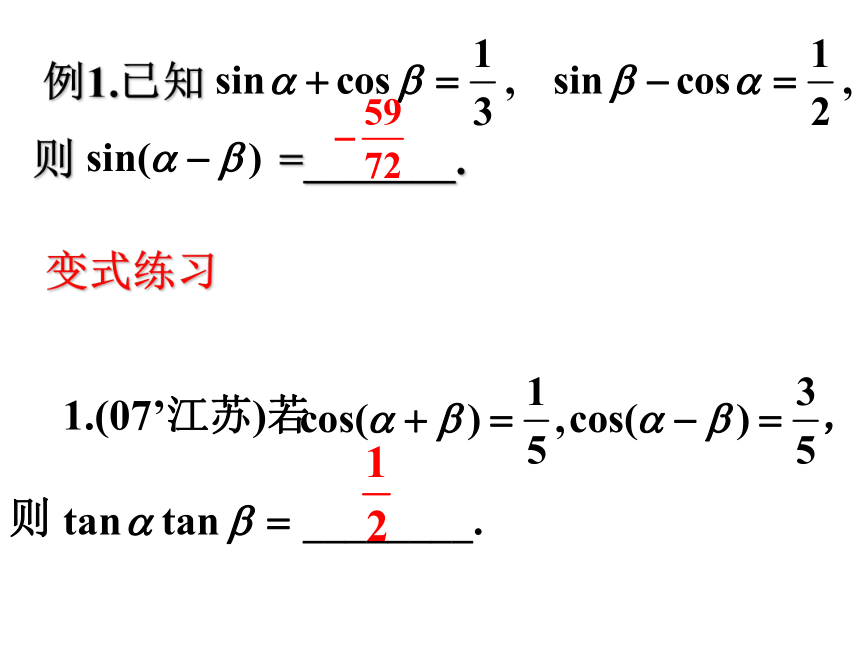



文档简介
课件21张PPT。三角恒等变换(1)问题:如何求Sin750=?和差角公式公式如何推导?体现了什么思想方法?二倍角公式降幂公式:题型一:直接应用公式1(2011辽宁)P67考题再现2
2(2011江苏)P67考题再现3 例1.已知
则 =_______.变式练习 1.(07’江苏)若
则 (3)tan17°+tan28°+tan17°tan28°=__.(4)(5)cos12°cos24°cos48°cos96°=______.例2.求值:(1) sin24°sin36°-cos24°cos36°=_____.(2) sin20°cos110°+ cos160°sin70°=_____.题型二:角的变换例3.已知
求 的值.P67例2的变形思考2[点评与警示] 在三角函数的化简、求值与证明中,常常对条件和结论进行恰当变换,以满足应用公式的条件.如常见的角的变换(如α=(α+β)-β=(α-β)+β,(α+β)+(α-β)=2α,
β= 1.已知
则 变式练习2. 若
则 的值等于( ) 小结 进行角之间的变换时,特别要注意考察待求问题中的角与已知条件中的角之间的联系 .巩固练习 1.已知 且
求2.已知
求 的值. 三角恒等变换(2)辅助角公式基础过关 1.(07’山东,5)函数 的最小正周期和最大值分别为( )巩固练习2.(10’浙江)
求函数
的值域和最小正周期.作 业1(12重庆文)= 4(2012年高考(北京理))已知函数(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
2(2011江苏)P67考题再现3 例1.已知
则 =_______.变式练习 1.(07’江苏)若
则 (3)tan17°+tan28°+tan17°tan28°=__.(4)(5)cos12°cos24°cos48°cos96°=______.例2.求值:(1) sin24°sin36°-cos24°cos36°=_____.(2) sin20°cos110°+ cos160°sin70°=_____.题型二:角的变换例3.已知
求 的值.P67例2的变形思考2[点评与警示] 在三角函数的化简、求值与证明中,常常对条件和结论进行恰当变换,以满足应用公式的条件.如常见的角的变换(如α=(α+β)-β=(α-β)+β,(α+β)+(α-β)=2α,
β= 1.已知
则 变式练习2. 若
则 的值等于( ) 小结 进行角之间的变换时,特别要注意考察待求问题中的角与已知条件中的角之间的联系 .巩固练习 1.已知 且
求2.已知
求 的值. 三角恒等变换(2)辅助角公式基础过关 1.(07’山东,5)函数 的最小正周期和最大值分别为( )巩固练习2.(10’浙江)
求函数
的值域和最小正周期.作 业1(12重庆文)= 4(2012年高考(北京理))已知函数(1)求f(x)的定义域及最小正周期;
(2)求f(x)的单调递增区间.
