广东省连州市连州中学高一数学《指数函数》课件
文档属性
| 名称 | 广东省连州市连州中学高一数学《指数函数》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 49.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 19:54:38 | ||
图片预览





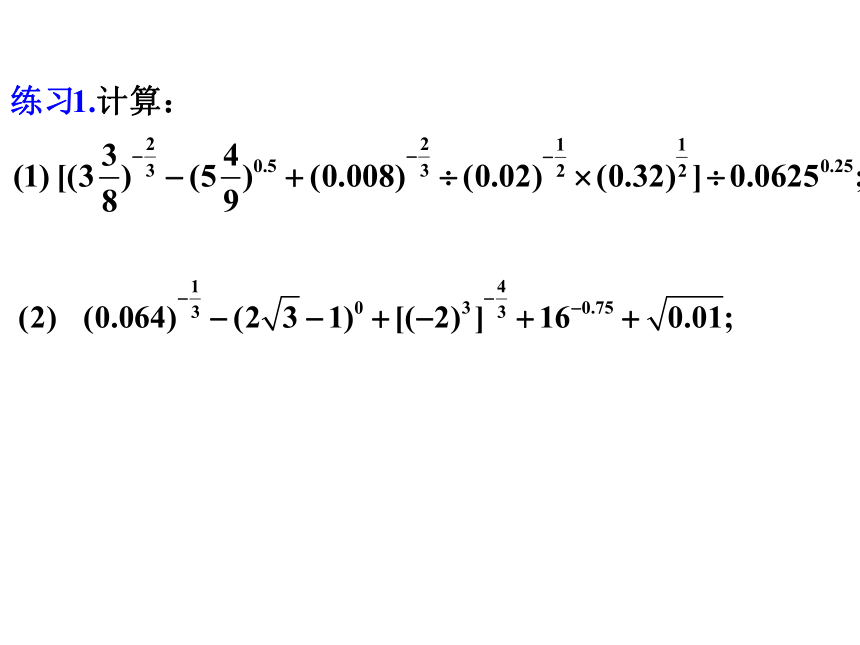
文档简介
课件18张PPT。 指数与指数函数考试要求:?
① 了解指数函数模型的实际背景.?
② 理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.?
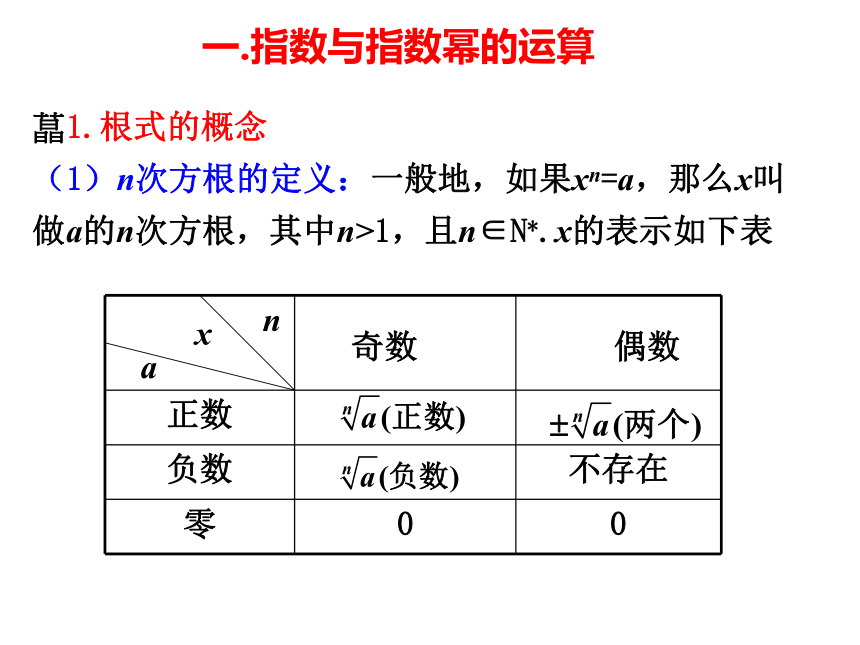
③ 理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点.?1.根式的概念
(1)n次方根的定义:一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*.x的表示如下表
nxa奇数 偶数一.指数与指数幂的运算2. 幂的运算:
③ ∈N*,且n>1);;⑤零的正分数指数幂等于零,零的负分数指数幂
没有意义.①②(1)有理数指数幂:④ ∈N*,且n>1);
(2)实数指数幂的性质(设a,b>0,r,s∈R)
①ar·as=ar+s;
②(ar)s=ars;
③(ab)r=ar·br.题型1.指数式的运算小结:一般进行指数幂运算时,化负指数为正指数,
化根式为分数指数,化小数为分数运算,同时兼顾
运算的顺序。对化简求值的结果,一般用分数指数
幂的形式保留。 一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.二.指数函数搭桥法;单调性法.题型2.比较大小方法:作直线x=1;
结论:看y轴右侧的图象
是底大图高,即底数越
大,越远离x轴正半轴.B题型3.指数函数图象及性质的应用BD2.函数f(x)=ax-b的图象如图所示,其中a、b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.00
D.0(2008·广州二模)设函数f(x)=a-|x| (a>0且a≠1),f(2)=4,则( )
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(1)>f(2) D.f(-2)>f(2)BA求下列函数的定义域和值域题型4 指数函数的综合问题[练习1] 练习2:
① 了解指数函数模型的实际背景.?
② 理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.?
③ 理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点.?1.根式的概念
(1)n次方根的定义:一般地,如果xn=a,那么x叫做a的n次方根,其中n>1,且n∈N*.x的表示如下表
nxa奇数 偶数一.指数与指数幂的运算2. 幂的运算:
③ ∈N*,且n>1);;⑤零的正分数指数幂等于零,零的负分数指数幂
没有意义.①②(1)有理数指数幂:④ ∈N*,且n>1);
(2)实数指数幂的性质(设a,b>0,r,s∈R)
①ar·as=ar+s;
②(ar)s=ars;
③(ab)r=ar·br.题型1.指数式的运算小结:一般进行指数幂运算时,化负指数为正指数,
化根式为分数指数,化小数为分数运算,同时兼顾
运算的顺序。对化简求值的结果,一般用分数指数
幂的形式保留。 一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.二.指数函数搭桥法;单调性法.题型2.比较大小方法:作直线x=1;
结论:看y轴右侧的图象
是底大图高,即底数越
大,越远离x轴正半轴.B题型3.指数函数图象及性质的应用BD2.函数f(x)=ax-b的图象如图所示,其中a、b为常数,则下列结论正确的是( )
A.a>1,b<0
B.a>1,b>0
C.0
D.0
A.f(-2)>f(-1) B.f(-1)>f(-2)
C.f(1)>f(2) D.f(-2)>f(2)BA求下列函数的定义域和值域题型4 指数函数的综合问题[练习1] 练习2:
