27.2相似三角形 课后练习 2021—2022学年人教版九年级数学下册(word版含答案)
文档属性
| 名称 | 27.2相似三角形 课后练习 2021—2022学年人教版九年级数学下册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 374.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 13:02:49 | ||
图片预览

文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似 27.2相似三角形 课后练习
一、选择题
1.下列各组条件中不能使△ABC与△DEF相似的是( )
A.∠A=∠D=40°,∠B=∠E=60°,AB=DE
B.∠A=∠D=60°,∠B= 40°,∠E=80°
C.∠A=∠D=50°,AB=3 ,AC=5 ,DE=6 ,DF=10
D.∠B=∠E=70°,AB:DE=AC:DF
2.若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A.1 B.2 C.3 D.4
3.如图,在中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断∽的是( ).
A. B. C. D.
4.如图, ∽ ,且 ,则 与 的相似比为( )
A.2:3 B.3:2 C.2:1 D.1:2
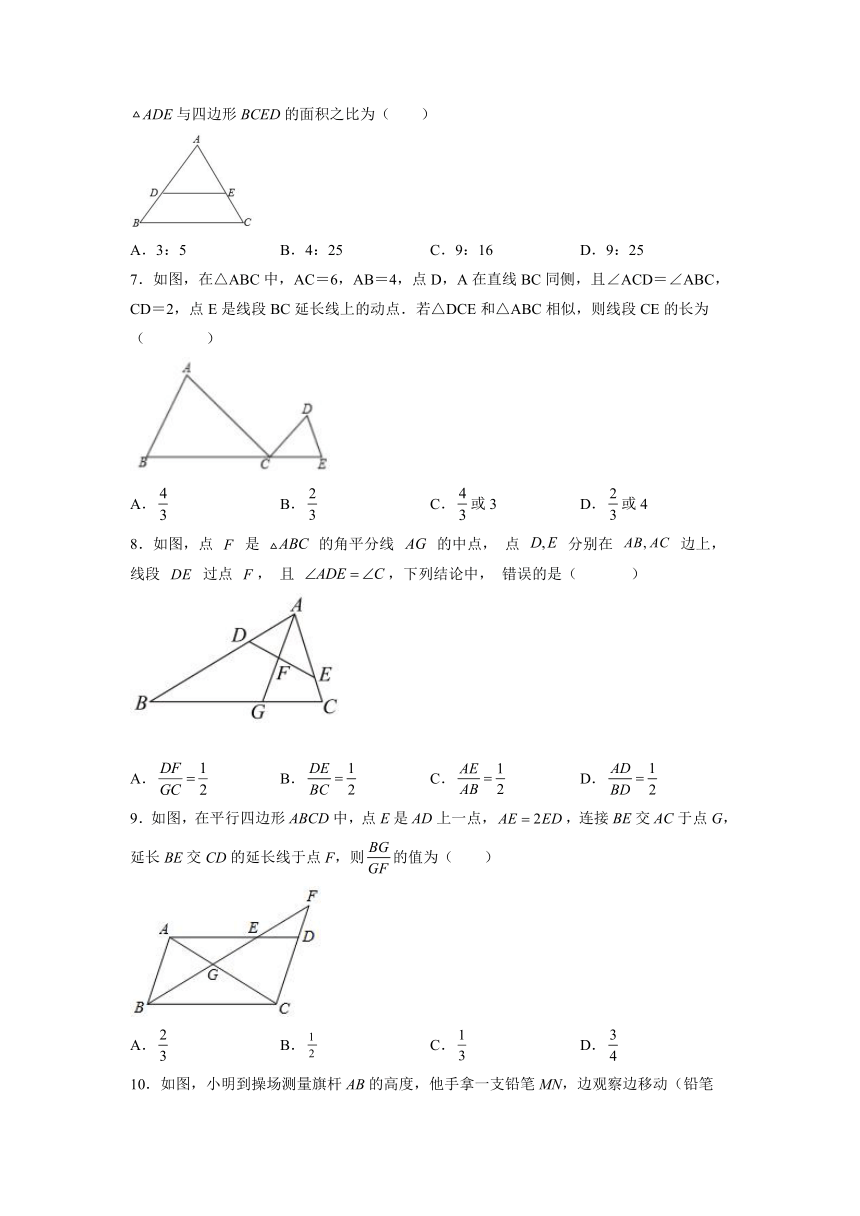
5.如下图,D、E分别是△ABC边的AB、AC上的点,DE∥BC,且S△ADE︰S△ABC=1︰9,那么AD∶BD的值为( )
A.1︰9 B.1︰3 C.1︰8 D.1︰2
6.在ABC中,D,E分别是边AB,AC上的两个点,并且DEBC,AD:BD=3:2,则ADE与四边形BCED的面积之比为( )
A.3:5 B.4:25 C.9:16 D.9:25
7.如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( )
A. B. C.或3 D.或4
8.如图,点 是 的角平分线 的中点, 点 分别在 边上,线段 过点 , 且 ,下列结论中, 错误的是( )
A. B. C. D.
9.如图,在平行四边形ABCD中,点E是AD上一点,,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A. B. C. D.
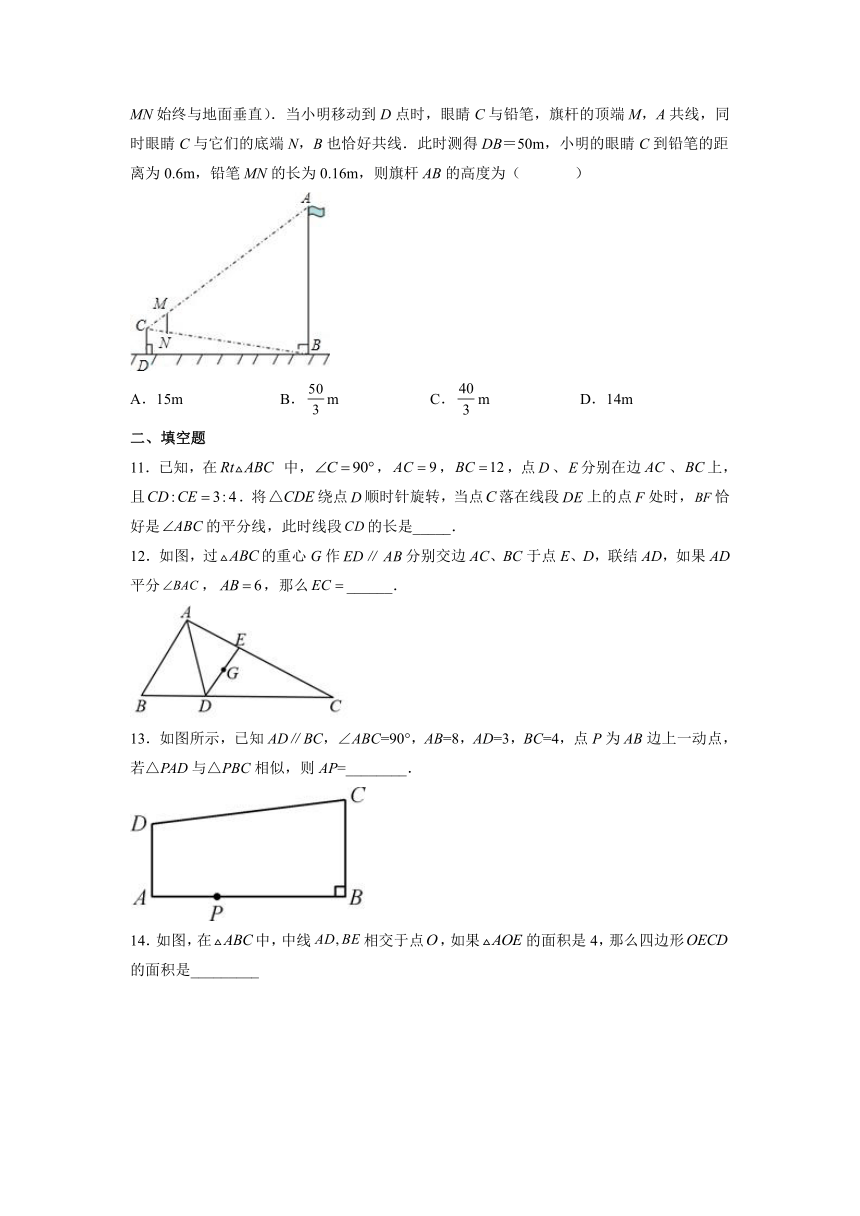
10.如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
二、填空题
11.已知,在 中,,,,点、分别在边、上,且.将绕点顺时针旋转,当点落在线段上的点处时,恰好是的平分线,此时线段的长是_____.
12.如图,过的重心G作分别交边AC、BC于点E、D,联结AD,如果AD平分,,那么______.
13.如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP=________.
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
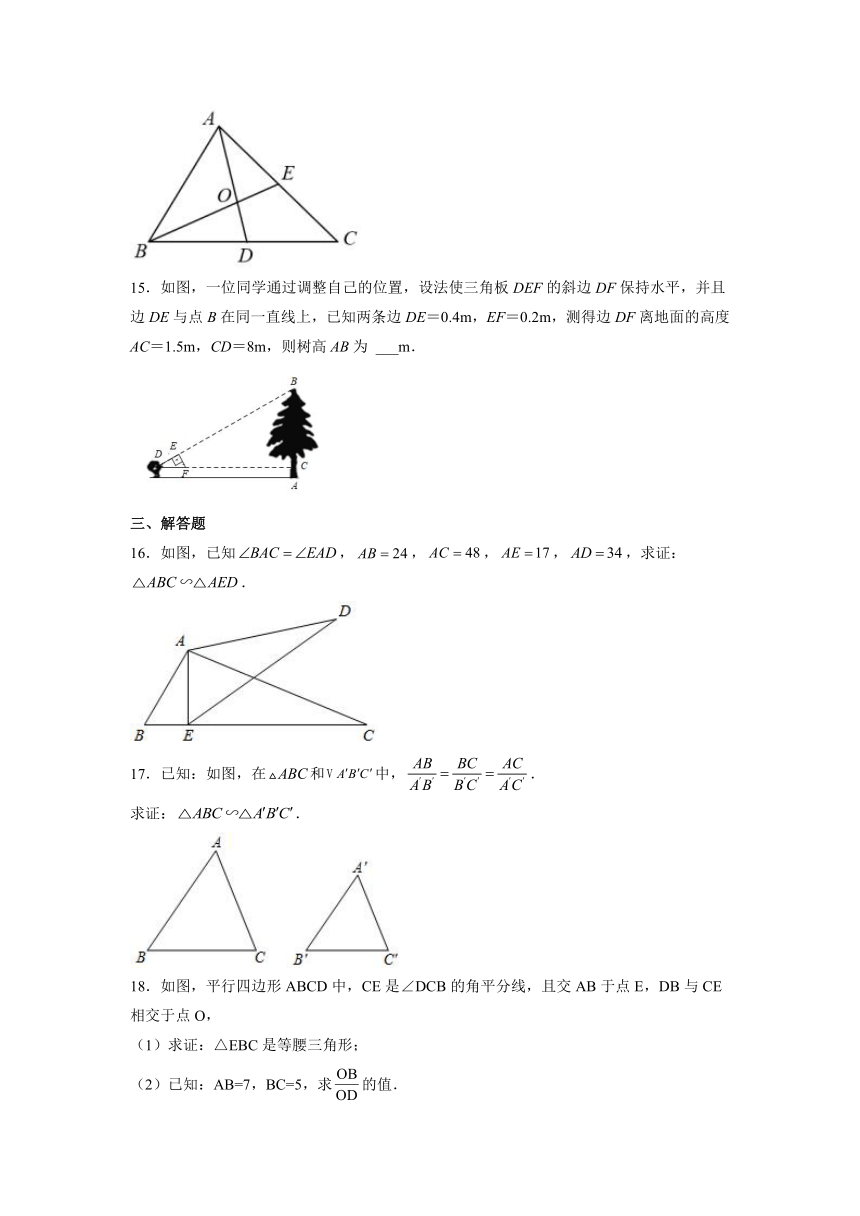
15.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 ___m.
三、解答题
16.如图,已知,,,,,求证:.
17.已知:如图,在和中,.
求证:.
18.如图,平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求的值.
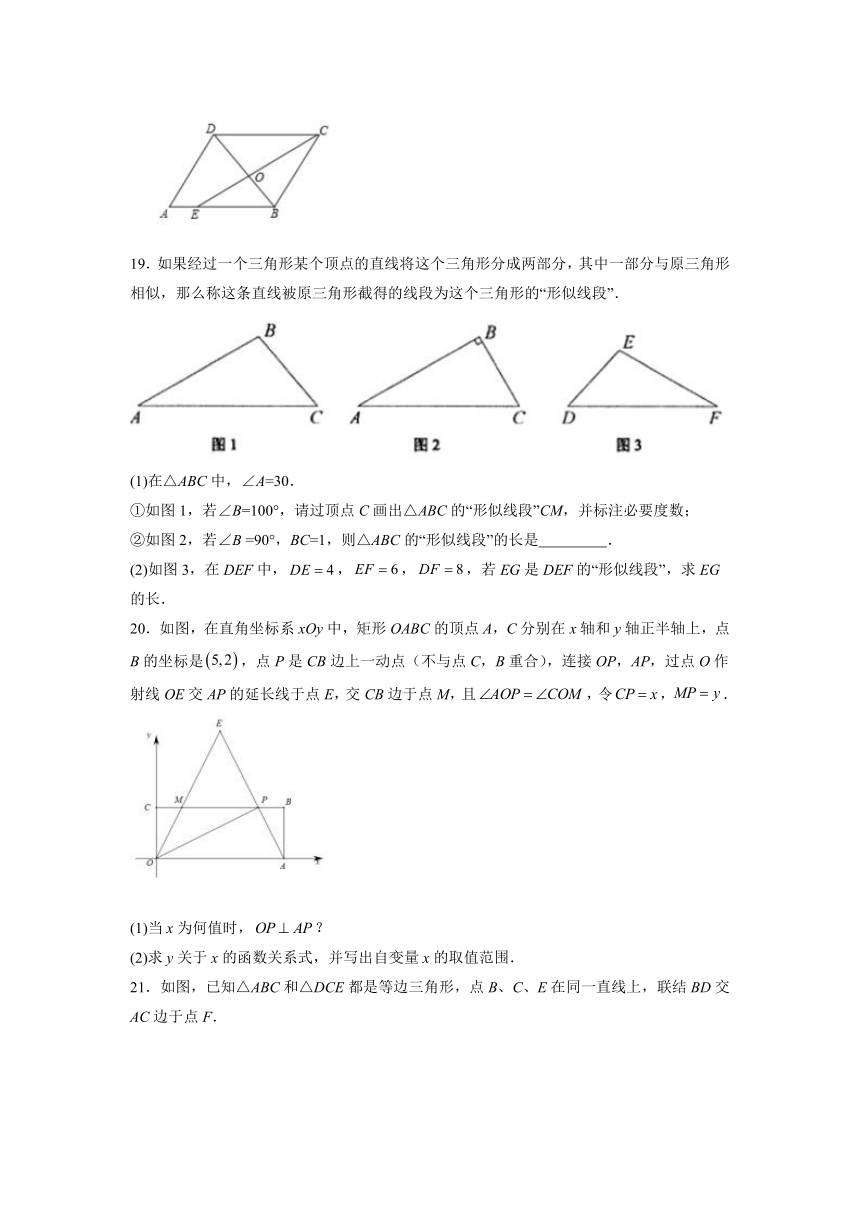
19.如果经过一个三角形某个顶点的直线将这个三角形分成两部分,其中一部分与原三角形相似,那么称这条直线被原三角形截得的线段为这个三角形的“形似线段”.
(1)在△ABC中,∠A=30.
①如图1,若∠B=100°,请过顶点C画出△ABC的“形似线段”CM,并标注必要度数;
②如图2,若∠B =90°,BC=1,则△ABC的“形似线段”的长是 .
(2)如图3,在DEF中,,,,若EG是DEF的“形似线段”,求EG的长.
20.如图,在直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴和y轴正半轴上,点B的坐标是,点P是CB边上一动点(不与点C,B重合),连接OP,AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且,令,.
(1)当x为何值时,?
(2)求y关于x的函数关系式,并写出自变量x的取值范围.
21.如图,已知△ABC和△DCE都是等边三角形,点B、C、E在同一直线上,联结BD交AC边于点F.
(1)如果∠ABD=∠CAD,求证:BF2=DF DB;
(2)如果AF=2FC,S四边形ABCD=18,求S△DCE的值.
22.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
23.【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下:
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
(1)已知榕树CD在路灯下的影子为DE,请画出榕树FG在路灯下的影子GH;
(2)如图①,若榕树CD的高度为3.6米,其离路灯的距离BD为6米,两棵榕树的影长DE,GH均为4米,两棵树之间的距离DG为6米,求榕树FG的高度;
(3)无论太阳光还是点光源,其本质与视线问题相同.日常生活中我们也可以直接利用视线解决问题.如图②,建筑物CD高为50米,建筑物MF上有一个广告牌EM,合计总高度EF为70米,两座建筑物之间的直线距离FD为30米.一个观测者(身高不计)先站在A处观测,发现能看见广告牌EM的底端M处,观测者沿着直线AF向前走了5米到B处观测,发现刚好看到广告牌EM的顶端E处.则广告牌EM的高度为 米
【参考答案】
1.D 2.C 3.C 4.A 5.D 6.C 7.C 8.D 9.A 10.C
11.6
12.8
13.或2或6
14.8
15.5.5
16.证明:,,,,
,
,
,
.
17.证明:在线段AB(或它的延长线)上截取AD=A′B′,过点D作DE∥BC,交AC于点E,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
又,AD=A′B′,
∴=,=,
∴DE=B′C′,AE=A′C′,
在△ADE和△A′B′C′中
,
∴△ADE≌△A′B′C′(SSS),
∴△ABC∽△A'B'C'.
18.解:(1)∵四边形ABCD是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,,
∴,
∴,
∵,,
∴,
∴.
19.(1)①如图所示,
②分论讨论如下:
当时,如下图:
,
,
,
,
当时,如下图:
设,则,
,
解得:,
,
则△ABC的“形似线段”的长是或,
故答案为:或.
(2)
解:①若,
则.
,,,
.
②若,
则.
,,,
.
综上,.
20.(1)点B的坐标是,四边形OABC是矩形,
,,,
解得
经检验都是方程的解
当时
,
则与线段交于点,如图,与题图不符,故舍去
(2)
当时,,
此时若,则点与重合,则,即
点P是CB边上一动点(不与点C,B重合),
21.(1)证明:∵△ABC和△DCE都是等边三角形,
∴AB=AC,∠BAC=∠DCE=∠ACB=∠ACD=60°,
又∵∠ABD=∠CAD,
∴△ABF≌△CAD(ASA),
∴BF=AD,
∵∠ADF=∠BDA,∠ABD=∠CAD,
∴△ADF∽△BDA,
∴,
∴AD2=DF BD,
∴BF2=DF BD;
(2)解:∵∠ACB=∠DCE=60°,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴,
∴△DCF∽△BAF,
∴=,
∴,,,
设S△DCF=x,则S△ADF=S△BCF=2x,S△ABF=4x,
∵S四边形ABCD=18,
∴x+2x+2x+4x=18,
解得x=2,
∴S△ABF=8,S△BCF=4,
∴S△ABC=S△ABF+S△BCF=8+4=12,
∵△ABC和△DCE都是等边三角形,
∴△ABC∽△DCE,
∴=,
∴S△DCE==×12=3.
22.解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
23.(1)解:图①中GH即为所求;
(2)∵CD∥PB,
∴△ECD∽△EPB,
∴,即,
解得:PB=9,
∵FG∥PB,
∴△HFG∽△HPB,
∴,即,
解得:FG=,
答:榕树FG的高度为米;
(3)∵CD∥EF,
∴△BCD∽△BEF,
∴,即,
解得:BD=75,
∵CD∥EF,
∴△ACD∽△AMF,
∴,即,
解得:MF=,
∴EM=EF-MF=70-=(米),
故答案为:.
一、选择题
1.下列各组条件中不能使△ABC与△DEF相似的是( )
A.∠A=∠D=40°,∠B=∠E=60°,AB=DE
B.∠A=∠D=60°,∠B= 40°,∠E=80°
C.∠A=∠D=50°,AB=3 ,AC=5 ,DE=6 ,DF=10
D.∠B=∠E=70°,AB:DE=AC:DF
2.若P是RtABC直角边BC(∠C=90 ,∠B≠∠A)上异于B、C的一点,过点P作直线截ABC,截得的三角形与原ABC相似,满足这样条件的直线有( )条
A.1 B.2 C.3 D.4
3.如图,在中,点D、E分别在AB、AC边上,DE与BC不平行,那么下列条件中,不能判断∽的是( ).
A. B. C. D.
4.如图, ∽ ,且 ,则 与 的相似比为( )
A.2:3 B.3:2 C.2:1 D.1:2
5.如下图,D、E分别是△ABC边的AB、AC上的点,DE∥BC,且S△ADE︰S△ABC=1︰9,那么AD∶BD的值为( )
A.1︰9 B.1︰3 C.1︰8 D.1︰2
6.在ABC中,D,E分别是边AB,AC上的两个点,并且DEBC,AD:BD=3:2,则ADE与四边形BCED的面积之比为( )
A.3:5 B.4:25 C.9:16 D.9:25
7.如图,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点.若△DCE和△ABC相似,则线段CE的长为( )
A. B. C.或3 D.或4
8.如图,点 是 的角平分线 的中点, 点 分别在 边上,线段 过点 , 且 ,下列结论中, 错误的是( )
A. B. C. D.
9.如图,在平行四边形ABCD中,点E是AD上一点,,连接BE交AC于点G,延长BE交CD的延长线于点F,则的值为( )
A. B. C. D.
10.如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
二、填空题
11.已知,在 中,,,,点、分别在边、上,且.将绕点顺时针旋转,当点落在线段上的点处时,恰好是的平分线,此时线段的长是_____.
12.如图,过的重心G作分别交边AC、BC于点E、D,联结AD,如果AD平分,,那么______.
13.如图所示,已知AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC相似,则AP=________.
14.如图,在中,中线相交于点,如果的面积是4,那么四边形的面积是_________
15.如图,一位同学通过调整自己的位置,设法使三角板DEF的斜边DF保持水平,并且边DE与点B在同一直线上,已知两条边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB为 ___m.
三、解答题
16.如图,已知,,,,,求证:.
17.已知:如图,在和中,.
求证:.
18.如图,平行四边形ABCD中,CE是∠DCB的角平分线,且交AB于点E,DB与CE相交于点O,
(1)求证:△EBC是等腰三角形;
(2)已知:AB=7,BC=5,求的值.
19.如果经过一个三角形某个顶点的直线将这个三角形分成两部分,其中一部分与原三角形相似,那么称这条直线被原三角形截得的线段为这个三角形的“形似线段”.
(1)在△ABC中,∠A=30.
①如图1,若∠B=100°,请过顶点C画出△ABC的“形似线段”CM,并标注必要度数;
②如图2,若∠B =90°,BC=1,则△ABC的“形似线段”的长是 .
(2)如图3,在DEF中,,,,若EG是DEF的“形似线段”,求EG的长.
20.如图,在直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴和y轴正半轴上,点B的坐标是,点P是CB边上一动点(不与点C,B重合),连接OP,AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且,令,.
(1)当x为何值时,?
(2)求y关于x的函数关系式,并写出自变量x的取值范围.
21.如图,已知△ABC和△DCE都是等边三角形,点B、C、E在同一直线上,联结BD交AC边于点F.
(1)如果∠ABD=∠CAD,求证:BF2=DF DB;
(2)如果AF=2FC,S四边形ABCD=18,求S△DCE的值.
22.如图1,在等腰中,,点D为斜边AB边上一动点(不含端点).作,DE,DF分别交AB,AC于点E和点F.请根据图形解答下面问题:
【问题发现】
(1)如图1,若点D为BC边中点.请直接写出DE,DF的数量关系_________.
【类比探究】
(2)如图2,若点D为BC边上一动点,且.猜想DF与DE的数量关系.并证明你的结论.
【拓展应用】
(3)如图3,在边长为4的等边中,点D为BC边上一动点,作.DE交AC边于点E.请问在点D的运动过程中,CE是否有最大值.如果有,求出最大值;如果没有,请说明理由.
23.【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下:
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
(1)已知榕树CD在路灯下的影子为DE,请画出榕树FG在路灯下的影子GH;
(2)如图①,若榕树CD的高度为3.6米,其离路灯的距离BD为6米,两棵榕树的影长DE,GH均为4米,两棵树之间的距离DG为6米,求榕树FG的高度;
(3)无论太阳光还是点光源,其本质与视线问题相同.日常生活中我们也可以直接利用视线解决问题.如图②,建筑物CD高为50米,建筑物MF上有一个广告牌EM,合计总高度EF为70米,两座建筑物之间的直线距离FD为30米.一个观测者(身高不计)先站在A处观测,发现能看见广告牌EM的底端M处,观测者沿着直线AF向前走了5米到B处观测,发现刚好看到广告牌EM的顶端E处.则广告牌EM的高度为 米
【参考答案】
1.D 2.C 3.C 4.A 5.D 6.C 7.C 8.D 9.A 10.C
11.6
12.8
13.或2或6
14.8
15.5.5
16.证明:,,,,
,
,
,
.
17.证明:在线段AB(或它的延长线)上截取AD=A′B′,过点D作DE∥BC,交AC于点E,
∵DE∥BC,
∴△ADE∽△ABC,
∴==,
又,AD=A′B′,
∴=,=,
∴DE=B′C′,AE=A′C′,
在△ADE和△A′B′C′中
,
∴△ADE≌△A′B′C′(SSS),
∴△ABC∽△A'B'C'.
18.解:(1)∵四边形ABCD是平行四边形,
∴,
∴,
∵平分,
∴,
∴,
∴,
∴是等腰三角形;
(2)∵,
∴,,
∴,
∴,
∵,,
∴,
∴.
19.(1)①如图所示,
②分论讨论如下:
当时,如下图:
,
,
,
,
当时,如下图:
设,则,
,
解得:,
,
则△ABC的“形似线段”的长是或,
故答案为:或.
(2)
解:①若,
则.
,,,
.
②若,
则.
,,,
.
综上,.
20.(1)点B的坐标是,四边形OABC是矩形,
,,,
解得
经检验都是方程的解
当时
,
则与线段交于点,如图,与题图不符,故舍去
(2)
当时,,
此时若,则点与重合,则,即
点P是CB边上一动点(不与点C,B重合),
21.(1)证明:∵△ABC和△DCE都是等边三角形,
∴AB=AC,∠BAC=∠DCE=∠ACB=∠ACD=60°,
又∵∠ABD=∠CAD,
∴△ABF≌△CAD(ASA),
∴BF=AD,
∵∠ADF=∠BDA,∠ABD=∠CAD,
∴△ADF∽△BDA,
∴,
∴AD2=DF BD,
∴BF2=DF BD;
(2)解:∵∠ACB=∠DCE=60°,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴,
∴△DCF∽△BAF,
∴=,
∴,,,
设S△DCF=x,则S△ADF=S△BCF=2x,S△ABF=4x,
∵S四边形ABCD=18,
∴x+2x+2x+4x=18,
解得x=2,
∴S△ABF=8,S△BCF=4,
∴S△ABC=S△ABF+S△BCF=8+4=12,
∵△ABC和△DCE都是等边三角形,
∴△ABC∽△DCE,
∴=,
∴S△DCE==×12=3.
22.解:(1)连接,如下图:
∵点D为BC边中点
∴
又∵为等腰直角三角形
∴,,
∴
又∵
∴
∴
∴
(2)分别过点、作、交于点
∵为等腰直角三角形
∴
又∵、
∴、为等腰直角三角形
∴,
∵,
∴
∴
∴
∴,,
∴,
∴
又∵
∴
∴,即
(3)∵,
∴
又∵
∴
∴
∴
设,
∴
∴当时,最大,最大为1.
23.(1)解:图①中GH即为所求;
(2)∵CD∥PB,
∴△ECD∽△EPB,
∴,即,
解得:PB=9,
∵FG∥PB,
∴△HFG∽△HPB,
∴,即,
解得:FG=,
答:榕树FG的高度为米;
(3)∵CD∥EF,
∴△BCD∽△BEF,
∴,即,
解得:BD=75,
∵CD∥EF,
∴△ACD∽△AMF,
∴,即,
解得:MF=,
∴EM=EF-MF=70-=(米),
故答案为:.
