广东省新兴县惠能中学高二数学《221直线与平面平行的判定》课件
文档属性
| 名称 | 广东省新兴县惠能中学高二数学《221直线与平面平行的判定》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-27 00:00:00 | ||
图片预览





文档简介
课件46张PPT。2.2.1直线与平面
平行的判定复习引入直线与平面有什么样的位置关系? 复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
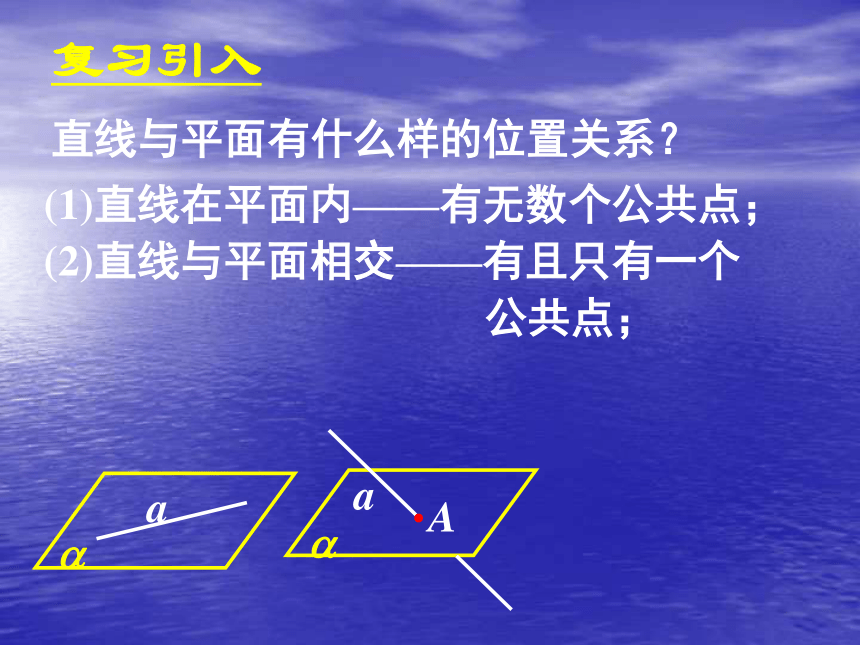
复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
(2)直线与平面相交——有且只有一个
公共点;
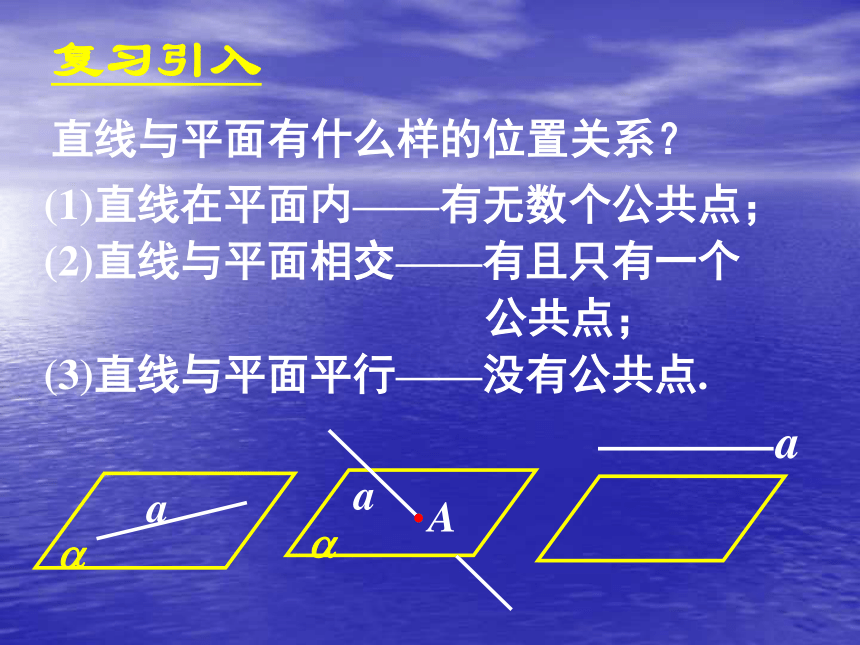
复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
(2)直线与平面相交——有且只有一个
公共点;
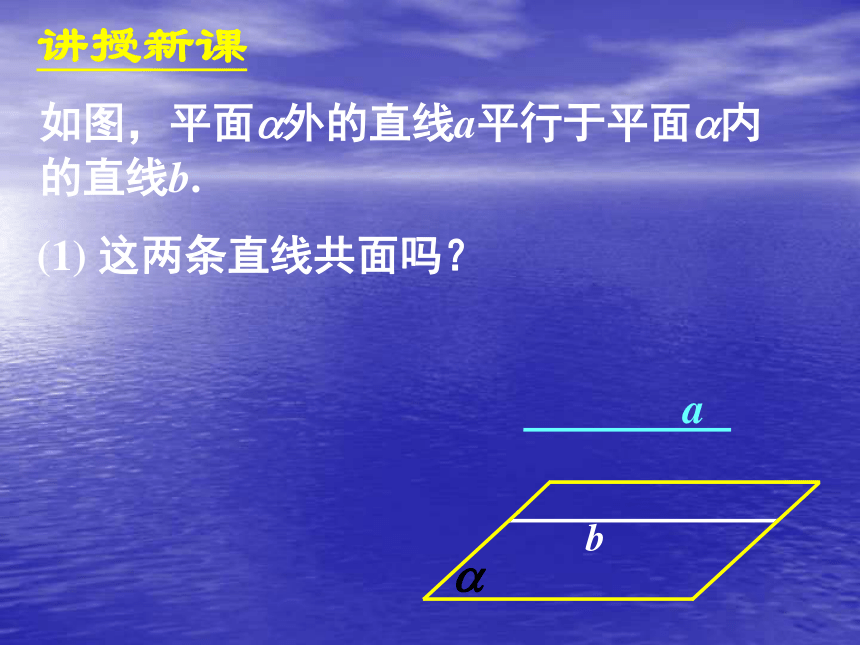
(3)直线与平面平行——没有公共点.讲授新课如图,平面?外的直线a平行于平面?内
的直线b.b(1) 这两条直线共面吗?
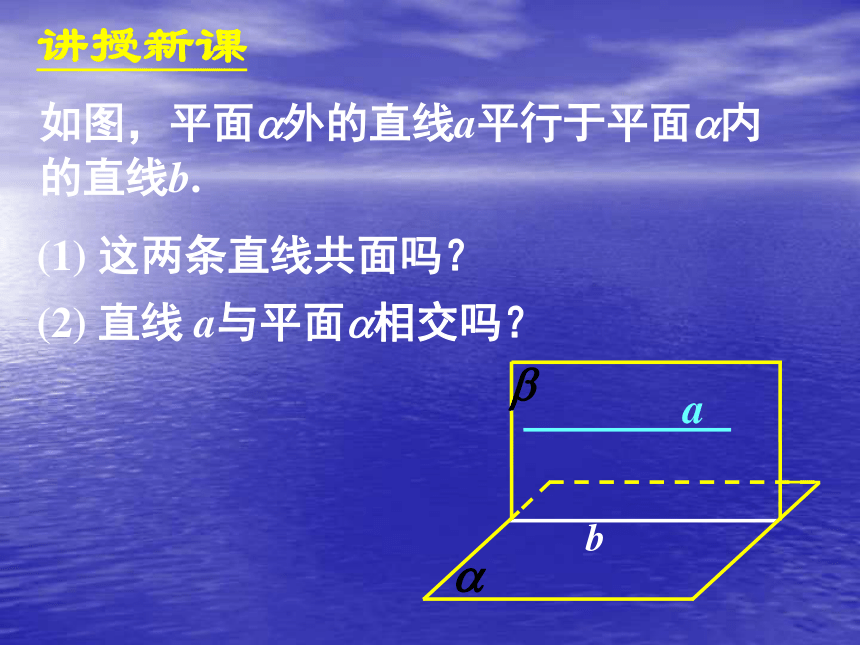
讲授新课如图,平面?外的直线a平行于平面?内
的直线b.b(1) 这两条直线共面吗?
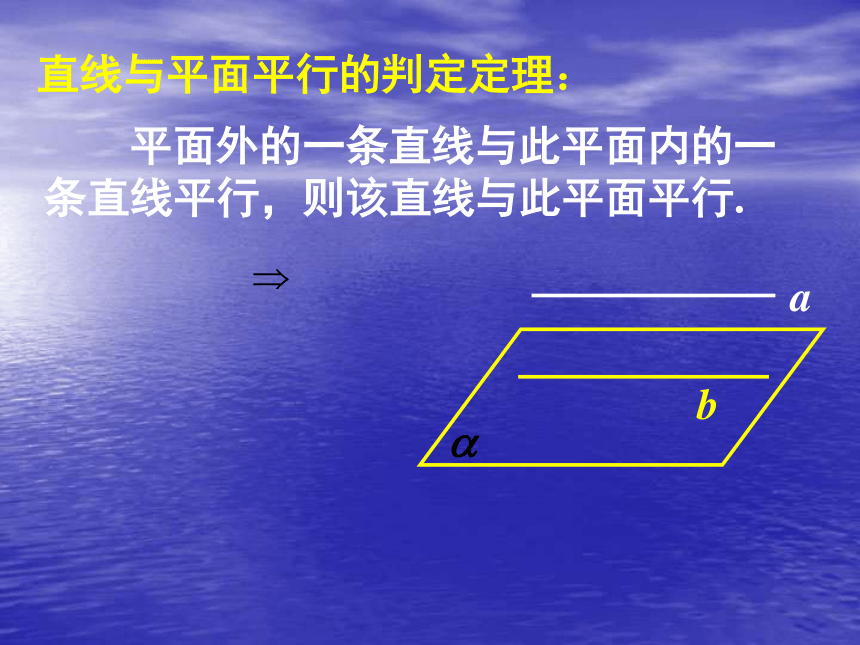
(2) 直线 a与平面?相交吗?直线与平面平行的判定定理: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.直线与平面平行的判定定理: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.直线与平面平行的判定定理: ab 平面外的一条直线与此平面内的一
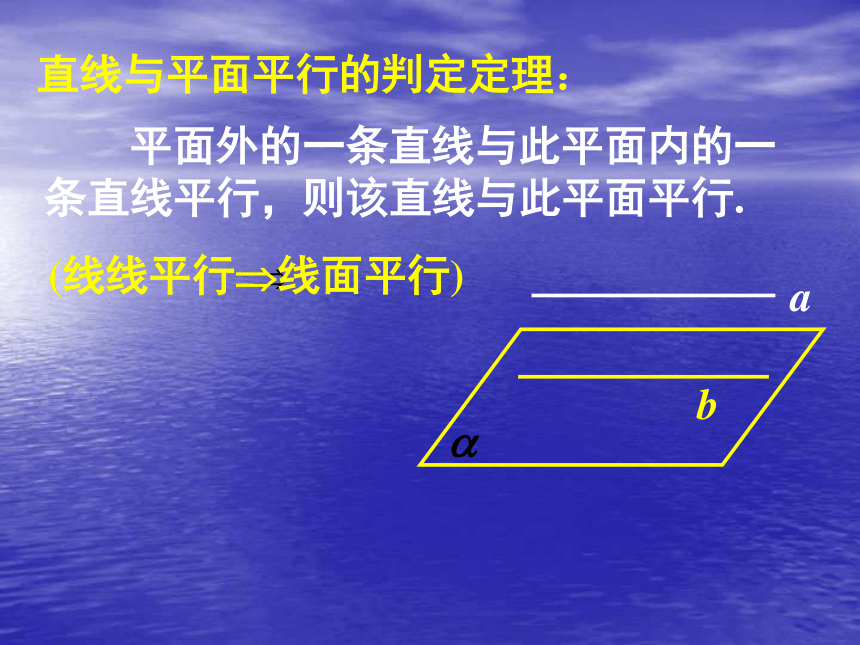
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab符号表示: 平面外的一条直线与此平面内的一
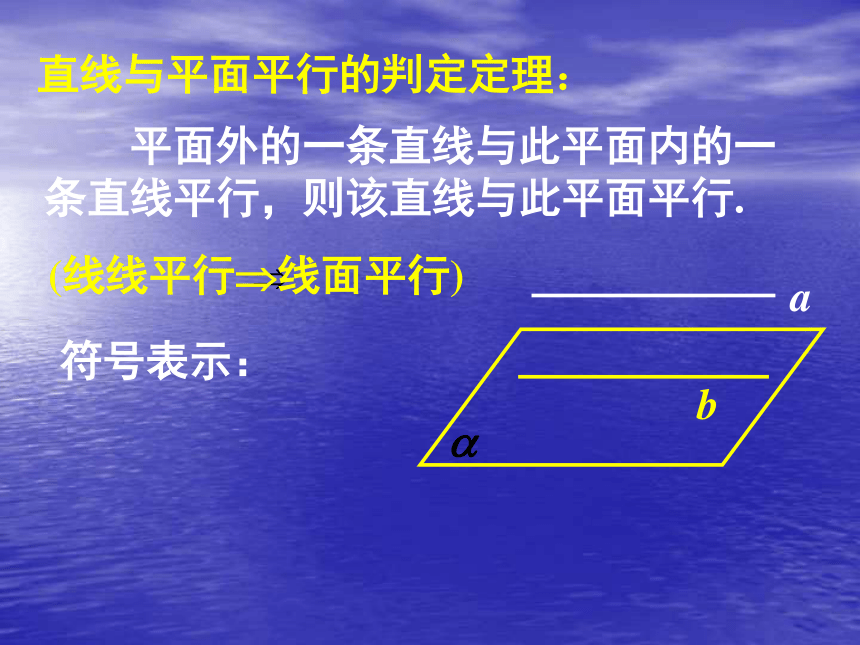
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab符号表示: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:球场地面练习A练习练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 平面BC1和平面A1C1 BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 平面BC1和平面A1C1 平面BC1和
平面DC1BD1C1A1B1ADC3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假真3. 判断命题的真假假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假真定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.ABCDEF定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.分析:要证明线面平行
只需证明线线平行,即
在平面BCD内找一条直
线平行于EF,由已知的
条件怎样找这条直线?ABCDEF定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.分析:要证明线面平行
只需证明线线平行,即
在平面BCD内找一条直
线平行于EF,由已知的
条件怎样找这条直线?ABCDEF________________.1.如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是变式1________________.1.如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是变式1EF//平面BCD变式2ABCDFOE2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.变式2ABCDFOE2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.分析:变式2ABCDFOE分析:连结OF,2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.变式2分析:△ABE的中位线,
所以得到AB//OF.ABCDFOE连结OF,2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:2. 寻找平行直线可以通过三角形的中位
线、梯形的中位线、平行线的判定等
来完成.
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:2. 寻找平行直线可以通过三角形的中位
线、梯形的中位线、平行线的判定等
来完成.3. 证明的书写三个条件“内”、“外”、
“平行”,缺一不可.1.如图,长方体ABCD-A1B1C1D1中,与
AA1平行的平面是___________________.巩固练习1.如图,长方体ABCD-A1B1C1D1中,与
AA1平行的平面是___________________.平面BC1 、平面CD1巩固练习巩固练习2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBA巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBA巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO作业:1、复习巩固今天的学习内容;
2、P62第3 题(做在作业本上);
3、 P62第2 题(做在书上)。
平行的判定复习引入直线与平面有什么样的位置关系? 复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
(2)直线与平面相交——有且只有一个
公共点;
复习引入直线与平面有什么样的位置关系? (1)直线在平面内——有无数个公共点;
(2)直线与平面相交——有且只有一个
公共点;
(3)直线与平面平行——没有公共点.讲授新课如图,平面?外的直线a平行于平面?内
的直线b.b(1) 这两条直线共面吗?
讲授新课如图,平面?外的直线a平行于平面?内
的直线b.b(1) 这两条直线共面吗?
(2) 直线 a与平面?相交吗?直线与平面平行的判定定理: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.直线与平面平行的判定定理: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.直线与平面平行的判定定理: ab 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab符号表示: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab符号表示: 平面外的一条直线与此平面内的一
条直线平行,则该直线与此平面平行.(线线平行?线面平行)直线与平面平行的判定定理: ab感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:感受校园生活中线面平行的例子:球场地面练习A练习练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 平面BC1和平面A1C1 BD1C1A1B1ADC练习2. 如图,长方体的六个面都是矩形,则(1)与直线AB平行的平面是:(2)与直线AD平行的平面是:(3)与直线AA1平行的
平面是:平面A1C1和平面DC1 平面BC1和平面A1C1 平面BC1和
平面DC1BD1C1A1B1ADC3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假3. 判断命题的真假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假真3. 判断命题的真假假练习(3)如果一直线与平面平行,则它与平面
内的任何直线平行.(2)过直线外一点,可以作无数个平面与
这条直线平行.(1)如果一条直线不在平面内,则这条直
线就与这个平面平行.假真定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.ABCDEF定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.分析:要证明线面平行
只需证明线线平行,即
在平面BCD内找一条直
线平行于EF,由已知的
条件怎样找这条直线?ABCDEF定理的应用例1. 如图,空间四边形ABCD中,E、F
分别是AB,AD的中点.
求证:EF∥平面BCD.分析:要证明线面平行
只需证明线线平行,即
在平面BCD内找一条直
线平行于EF,由已知的
条件怎样找这条直线?ABCDEF________________.1.如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是变式1________________.1.如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是变式1EF//平面BCD变式2ABCDFOE2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.变式2ABCDFOE2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.分析:变式2ABCDFOE分析:连结OF,2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.变式2分析:△ABE的中位线,
所以得到AB//OF.ABCDFOE连结OF,2. 如图,四棱锥A—DBCE中,O为底面
正方形DBCE对角线的交点,F为AE的
中点. 求证: AB//平面DCF.
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:2. 寻找平行直线可以通过三角形的中位
线、梯形的中位线、平行线的判定等
来完成.
1. 线面平行,通常可以转化为线线平行
来处理.反思~领悟:2. 寻找平行直线可以通过三角形的中位
线、梯形的中位线、平行线的判定等
来完成.3. 证明的书写三个条件“内”、“外”、
“平行”,缺一不可.1.如图,长方体ABCD-A1B1C1D1中,与
AA1平行的平面是___________________.巩固练习1.如图,长方体ABCD-A1B1C1D1中,与
AA1平行的平面是___________________.平面BC1 、平面CD1巩固练习巩固练习2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBA巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBA巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO巩固练习 分析:要证BD1//
平面AEC,即要在平
面AEC内找一条直线
与BD1平行.根据已知
条件应该怎样考虑辅
助线?2. 如图,正方体ABCD-A1B1C1D1中,E
为DD1的中点,求证:BD1//平面AEC.ED1C1B1A1DCBAO作业:1、复习巩固今天的学习内容;
2、P62第3 题(做在作业本上);
3、 P62第2 题(做在书上)。
