江苏省苏州市常熟市高一下学期开学考试数学试题(word版含解析)
文档属性
| 名称 | 江苏省苏州市常熟市高一下学期开学考试数学试题(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 726.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-12 15:48:33 | ||
图片预览



文档简介
江苏省苏州市常熟市高一下学期开学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点为椭圆的一个焦点,过点作圆的两条切线,若这两条切线互相垂直,则( )
A.2 B. C. D.
2.在中,所对的边为,,则面积的最大值为
A.3 B.6 C. D.
3.已知函数满足,则直线的斜率为
A.1 B. C. D.
4.若,则( )
A. B. C. D.
5.如图所示,位于东海某岛的雷达观测站A,发现其北偏东方向,距离海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北方向的C处,且已知A,C之间的距离为10海里,则该货船的速度大小为( )
A.海里/小时 B.海里/小时
C.海里/小时 D.海里/小时
6.在中,下列等式中总能成立的是( )
A. B. C. D.
7.已知一组数据的平均数是1,那么另一组数据的平均数为( )
A.4 B.3 C.2 D.1
8.以平面直角坐标系的原点为极点,轴的正半轴为极轴,建立极坐标系,两周坐标系中取相同长度单位,已知直线参数方程是(为参数),圆极坐标方程是,则直线被选截得弦长为( )
A. B. C. D.
9.已知三条直线,,不能构成三角形,则实数的取值集合为( )
A. B.
C. D.
10.已知圆上任意一点关于直线的对称点也在圆上,则的值为
A. B. C. D.
11.某防疫站对学生进行身体健康调查,与采用分层抽样的办法抽取样本.某中学共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学共有女生
A.1030人 B.97人 C.950人 D.970人
12.如图,在正方形中,为的中点,是以为直径的半圆弧上任意一点,设,则的最小值为( )
A. B.1 C.2 D.3
二、填空题
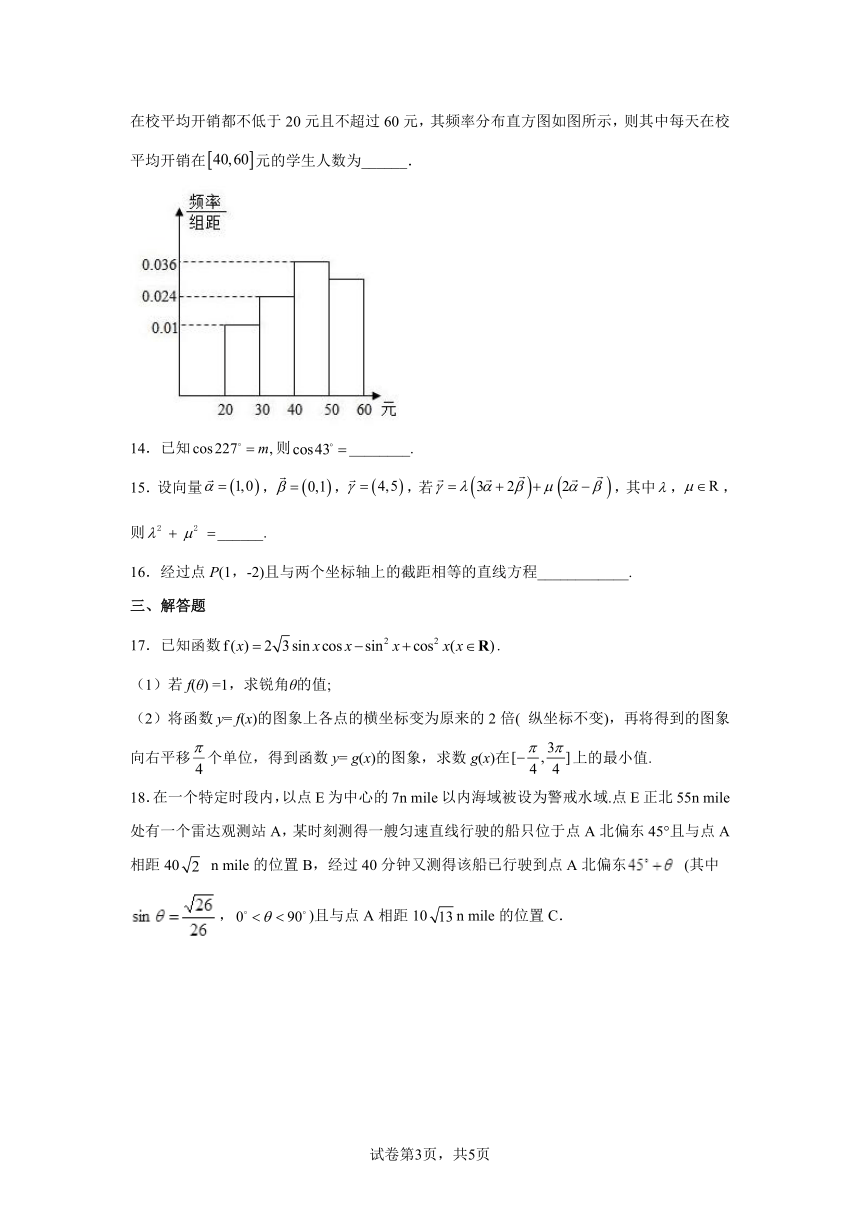
13.某学校为了了解住校学生每天在校平均开销情况,随机抽取了500名学生,他们的每天在校平均开销都不低于20元且不超过60元,其频率分布直方图如图所示,则其中每天在校平均开销在元的学生人数为______.
14.已知则________.
15.设向量,,,若,其中,,则______.
16.经过点P(1,-2)且与两个坐标轴上的截距相等的直线方程____________.
三、解答题
17.已知函数.
(1)若f(θ) =1,求锐角θ的值;
(2)将函数y= f(x)的图象上各点的横坐标变为原来的2倍( 纵坐标不变),再将得到的图象向右平移个单位,得到函数y= g(x)的图象,求数g(x)在上的最小值.
18.在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东 (其中,)且与点A相距10n mile的位置C.
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
19.已知圆C:,直线l:(m∈R).
(1)求证不论m取什么实数,直线l与圆恒交于两点;
(2)求直线被圆C截得的弦长最小时的l的方程.
20.已知函数在区间上的最大值为2.
(1)求函数在区间上的值域;
(2)设,求的值.
21.由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
(1)求的值;
(2)求地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出地区200家实体店经济损失的平均数与6000的大小关系.
22.已知圆,直线过点且与圆相切 .
(I)求直线的方程;
(II)如图,圆与轴交于两点,点是圆上异于的任意一点,过点且与轴垂直的直线为,直线交直线于点,直线交直线于点,求证:以为直径的圆与轴交于定点,并求出点的坐标 .
试卷第页,共页
试卷第页,共页
参考答案:
1.C
【解析】
根据切线垂直,推导出点至坐标原点的距离,即可求得焦点坐标和
【详解】
由题可设,根据题意,作图如下:
因为过点的两条切线垂直,
故可得,则,
故可得,即点坐标为.
则,
故,解得.
故选:C.
2.A
【解析】
【分析】
由正弦定理得,再由余弦定理得,从而求得,再根据面积及二次函数的最值求出答案.
【详解】
解:∵,
由正弦定理得,
∵,
∴由余弦定理得,,
∴,
∵,
∴,
∴面积,
当且仅当即时取等号,
故选:A.
【点睛】
本题主要考查正弦定理和余弦定理的应用,考查三角形的面积公式及其应用,考查二次函数的最值,考查计算能力,属于中档题.
3.A
【解析】
由已知抽象表达式知函数的对称轴为,利用函数图象的对称性,由.即可解得,而直线的斜率恰为,从而得解
【详解】
解:函数满足,
即为函数的对称轴,
即,
直线的斜率为
直线的斜率为1
故选:.
【点睛】
本题主要考查了三角函数的对称性及其应用,直线的斜率的定义和计算,特殊值代入的方法解函数图象对称性的技巧,属于基础题.
4.C
【解析】
【分析】
由题意利用诱导公式,同角三角函数的基本关系,二倍角公式,即可求解.
【详解】
因为,
所以,
故选:C
5.A
【解析】
【分析】
根据所给条件求出,再借助余弦定理即可作答.
【详解】
因,则,由题意得,
即,
在中,,,
由余弦定理得:
即,解得,
设船速为x,则,即,
所以货船的速度大小为海里小时.
故选:A
6.D
【解析】
【分析】
根据正弦定理辨析即可.
【详解】
对于A,由可得,,不一定成立,故A错误;
对于B,由可得,,不一定成立,故B错误;
对于C,由可得,,即,不一定成立,故C错误;
对于D,由正弦定理可得,,即一定成立,故D正确.
故选:D.
7.C
【解析】
【分析】
根据平均数公式计算可得;
【详解】
解:因为一组数据的平均数是1,所以
即,所以,即一组数据的平均数为;
故选:C
8.D
【解析】
【分析】
先求出直线与圆的直角坐标方程,求出半径和弦心距,再利用弦长公式求得弦长.
【详解】
直线参数方程是(为参数),
化为直角坐标方程为,
圆极坐标方程是,
化为直角坐标方程为,
即,表示以为圆心,半径,
弦心距,
弦长为.
故选:D
【点睛】
本题主要考查了参数方程与直角坐标方程的互化、极坐标方程与直角坐标方程的互化以及直线与圆相交弦长的几何求法,属于基础题.
9.D
【解析】
【分析】
根据题意得到直线与直线和直线分别平行时或直线过直线和直线的交点时,三条直线不能构成三角形,再分别计算相应的值即可.
【详解】
由题知:
①当直线与直线平行时,三条直线不能构成三角形.
即.
②当直线与直线平行时,三条直线不能构成三角形.
即.
③当直线过直线与直线交点时,
三条直线不能构成三角形.
所以,解得,
将代入,解得.
所以实数的取值集合为.
故选:D.
10.B
【解析】
【详解】
分析:圆上任意一点关于某直线的对称点还在圆上,说明该直线必过圆心,
根据圆心表达式求出圆心坐标,代入直线方程,即可求得m.
详解:由题意知,直线必过圆心,由圆心表达式可得圆心坐标为,
代入直线,解得.故选B.
点睛:圆的一般方程中,圆心坐标为,
圆的对称轴为过圆心的任意直线,可知直线过圆心.
11.D
【解析】
【详解】
由分层抽样的办法可知在名学生中抽取的男生有,故女生人数为,应选答案D.
12.B
【解析】
建立平面直角坐标系,设,利用坐标法将用点坐标表示,即可求出的最小值.
【详解】
以点为坐标原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系,
设,,则,,,半圆的方程为,
所以,,,
因为,即,
所以,即,
所以,又是半圆上的任意一点,
所以,,,
所以,所以当时,取得最小值.
故选:B
【点睛】
关键点点睛:本题主要考查二元变量的最值求法,关键是根据已知把几何图形放在适当的坐标系中,把有关点与向量用坐标表示,这样就能进行相应的代数运算和向量运算,从而使问题得到解决.
13.
【解析】
【分析】
由频率分布直方图得每天在校平均开销在元的学生的频率为,由此能求出每天在校平均开销在元的学生人数.
【详解】
解:由频率分布直方图得:
每天在校平均开销在元的学生的频率为:
,
每天在校平均开销在元的学生人数为:
.
故答案为330.
【点睛】
本题考查频数的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
14.;
【解析】
【分析】
先用诱导公式转化
得到,再用平关系求解.
【详解】
因为
所以
所以.
故答案为:.
【点睛】
本题主要考查了诱导公式和同角三角函数基本关系式,还考查了转化化归的思想和运算求解的能力,属于基础题.
15.5
【解析】
【分析】
整理,则,进而求解.
【详解】
由题,,
所以,解得,
所以,
故答案为:5
【点睛】
本题考查平面向量加法的坐标运算,属于基础题.
16.或
【解析】
分类讨论:截距等于或截距不等于,设出截距式,将点代入即可求解.
【详解】
当直线的截距等于时,即直线过,
所以直线的斜率,
所以直线方程为:,即;
当直线的截距不等于时, 设直线为,
将点P(1,-2)代入方程可得,所以,
所以直线方程为,即.
故答案为:或
【点睛】
本题考查了直线的截距式方程,考查了基本运算能力以及分类讨论的思想,属于基础题.
17.(1);(2)
【解析】
(1)首先利用三角恒等变换将函数化简,再结合,代入计算可得;
(2)根据三角函数的变换规则得到,再根据的取值范围,得到的取值范围,结合正弦函数的性质计算可得;
【详解】
解:
即
(1)
所以
所以或,
解得或,
因为为锐角,所以
(2)将各点的横坐标变为原来的2倍( 纵坐标不变)得到,再将的图象向右平移个单位得到,即
因为,所以
所以当,即时函数取得最小值
【点睛】
本题考查三角恒等变换与三角函数的性质的综合应用,考查三角函数的变换,属于中档题.
18.(I)船的行驶速度为(海里/小时).(II)船会进入警戒水域.
【解析】
【详解】
试题分析:(I)根据同角三角函数的基本关系式求出,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
(II)判断船是否会进入警戒水域,关键是看点E到直线l的距离与半径7的关系,因而可求出直线l的方程,以及E点坐标,然后再根据点到直线的距离公式得到结论.
(I)如图,AB=40,AC=10,
由于,所以cos=
由余弦定理得BC=
所以船的行驶速度为(海里/小时).
(II)解法一 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1=AB=40,
x2=ACcos,
y2=ACsin
所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=
所以船会进入警戒水域.
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,
==.
从而
在中,由正弦定理得,AQ=
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EPBC于点P,则EP为点E到直线BC的距离.
在Rt中,PE=QE·sin
=所以船会进入警戒水域.
考点:正余弦定理在解三角形当中的应用,直线方程,点到直线的距离,直线与圆的位置关系.
点评:掌握正余弦定理及能解决的三角形类型是解三角形的前提.第(II)问关键是知道如何判断船是否会进入警戒水域,实质是直线与圆的位置关系的判断.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)由l的方程得,根据m∈R可得定点,再根据求出|AC|与半径比较大小可得答案;
(2)由题意可知弦长最小时 ,求出,由点斜式方程可得答案.
(1)
证明:
由l的方程为,
所以解得,
即l恒过定点,
因为圆心为,所以(半径),所以点A在圆C内,从而直线l与圆C恒交于两点.
(2)
由题意可知弦长最小时 ,
因为,所以l的斜率为2,又l过点,由点斜式方程可得l的方程为.
20.(1) ;(2).
【解析】
【详解】
试题分析:(1)化简.由当时,取最大值当时,取最小值值域为;(2)由
.
试题解析:.
(1),∴,
则当,即时,取最大值,即有,得.
∴,则当,即时,取最小值.
∴值域为.
(2),
∴,
,∴,
∴.
考点:1、三角函数的图象与性质;2、三角恒等变换.
21.(1);(2)众数为3000,中位数为;(3)
【解析】
(1)根据概率和为1计算得到答案.
(2)计算众数和中位数得到答案.
(3)直接根据概率分布直方图得到答案.
【详解】
(1)依题意,,解得.
(2)由图可知,地区200家实体店该品牌洗衣机的月经济损失的众数为3000,
第一块小矩形的面积,第二块小矩形的面积,
故所求中位数在之间,所求中位数为.
(3)直接根据概率分布直方图得到:.
【点睛】
本题考查频率分布直方图、样本的数字特征,考查运算求解能力以及必然与或然思想.
22.(1).
(2)证明见解析;定点或.
【解析】
【分析】
(1)由已知中直线过点,我们可以设出直线的点斜式方程,化为一般式方程后,代入点到直线距离公式,根据直线与圆相切,圆心到直线的距离等于半径,可以求出k的值,进而得到直线的方程;
(2)由已知我们易求出P,Q两个点的坐标,设出M点的坐标,我们可以得到点P与Q的坐标,进而得到以为直径的圆的方程,根据圆的方程即可判断结论.
【详解】
(Ⅰ)由题意得,直线的斜率存在.
设直线的方程为.
因为直线与圆相切,
所以.
所以.
所以直线方程为.
(Ⅱ)由题意得,点,点.
设点,则.
直线的方程为.
所以直线与直线的交点为点.
直线的方程为.
所以直线与直线的交点为点.
设点.
则,.
因为以为直径的圆与轴交于定点,
所以
解得.
所以定点或.
【点睛】
该题考查的是有关直线与圆的方程的应用问题,涉及到的知识点有过圆外一点圆的切线方程的求法,圆与直线的交点,直线方程的点斜式,圆的方程的问题,直径所对的圆周角为直角,垂直应用向量的数量积等于零等,认真分析题意,求得结果.
试卷第页,共页
试卷第页,共页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知点为椭圆的一个焦点,过点作圆的两条切线,若这两条切线互相垂直,则( )
A.2 B. C. D.
2.在中,所对的边为,,则面积的最大值为
A.3 B.6 C. D.
3.已知函数满足,则直线的斜率为
A.1 B. C. D.
4.若,则( )
A. B. C. D.
5.如图所示,位于东海某岛的雷达观测站A,发现其北偏东方向,距离海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北方向的C处,且已知A,C之间的距离为10海里,则该货船的速度大小为( )
A.海里/小时 B.海里/小时
C.海里/小时 D.海里/小时
6.在中,下列等式中总能成立的是( )
A. B. C. D.
7.已知一组数据的平均数是1,那么另一组数据的平均数为( )
A.4 B.3 C.2 D.1
8.以平面直角坐标系的原点为极点,轴的正半轴为极轴,建立极坐标系,两周坐标系中取相同长度单位,已知直线参数方程是(为参数),圆极坐标方程是,则直线被选截得弦长为( )
A. B. C. D.
9.已知三条直线,,不能构成三角形,则实数的取值集合为( )
A. B.
C. D.
10.已知圆上任意一点关于直线的对称点也在圆上,则的值为
A. B. C. D.
11.某防疫站对学生进行身体健康调查,与采用分层抽样的办法抽取样本.某中学共有学生2000名,抽取了一个容量为200的样本,样本中男生103人,则该中学共有女生
A.1030人 B.97人 C.950人 D.970人
12.如图,在正方形中,为的中点,是以为直径的半圆弧上任意一点,设,则的最小值为( )
A. B.1 C.2 D.3
二、填空题
13.某学校为了了解住校学生每天在校平均开销情况,随机抽取了500名学生,他们的每天在校平均开销都不低于20元且不超过60元,其频率分布直方图如图所示,则其中每天在校平均开销在元的学生人数为______.
14.已知则________.
15.设向量,,,若,其中,,则______.
16.经过点P(1,-2)且与两个坐标轴上的截距相等的直线方程____________.
三、解答题
17.已知函数.
(1)若f(θ) =1,求锐角θ的值;
(2)将函数y= f(x)的图象上各点的横坐标变为原来的2倍( 纵坐标不变),再将得到的图象向右平移个单位,得到函数y= g(x)的图象,求数g(x)在上的最小值.
18.在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40 n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东 (其中,)且与点A相距10n mile的位置C.
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
19.已知圆C:,直线l:(m∈R).
(1)求证不论m取什么实数,直线l与圆恒交于两点;
(2)求直线被圆C截得的弦长最小时的l的方程.
20.已知函数在区间上的最大值为2.
(1)求函数在区间上的值域;
(2)设,求的值.
21.由于受到网络电商的冲击,某品牌的洗衣机在线下的销售受到影响,承受了一定的经济损失,现将地区200家实体店该品牌洗衣机的月经济损失统计如图所示.
(1)求的值;
(2)求地区200家实体店该品牌洗衣机的月经济损失的众数以及中位数;
(3)不经过计算,直接给出地区200家实体店经济损失的平均数与6000的大小关系.
22.已知圆,直线过点且与圆相切 .
(I)求直线的方程;
(II)如图,圆与轴交于两点,点是圆上异于的任意一点,过点且与轴垂直的直线为,直线交直线于点,直线交直线于点,求证:以为直径的圆与轴交于定点,并求出点的坐标 .
试卷第页,共页
试卷第页,共页
参考答案:
1.C
【解析】
根据切线垂直,推导出点至坐标原点的距离,即可求得焦点坐标和
【详解】
由题可设,根据题意,作图如下:
因为过点的两条切线垂直,
故可得,则,
故可得,即点坐标为.
则,
故,解得.
故选:C.
2.A
【解析】
【分析】
由正弦定理得,再由余弦定理得,从而求得,再根据面积及二次函数的最值求出答案.
【详解】
解:∵,
由正弦定理得,
∵,
∴由余弦定理得,,
∴,
∵,
∴,
∴面积,
当且仅当即时取等号,
故选:A.
【点睛】
本题主要考查正弦定理和余弦定理的应用,考查三角形的面积公式及其应用,考查二次函数的最值,考查计算能力,属于中档题.
3.A
【解析】
由已知抽象表达式知函数的对称轴为,利用函数图象的对称性,由.即可解得,而直线的斜率恰为,从而得解
【详解】
解:函数满足,
即为函数的对称轴,
即,
直线的斜率为
直线的斜率为1
故选:.
【点睛】
本题主要考查了三角函数的对称性及其应用,直线的斜率的定义和计算,特殊值代入的方法解函数图象对称性的技巧,属于基础题.
4.C
【解析】
【分析】
由题意利用诱导公式,同角三角函数的基本关系,二倍角公式,即可求解.
【详解】
因为,
所以,
故选:C
5.A
【解析】
【分析】
根据所给条件求出,再借助余弦定理即可作答.
【详解】
因,则,由题意得,
即,
在中,,,
由余弦定理得:
即,解得,
设船速为x,则,即,
所以货船的速度大小为海里小时.
故选:A
6.D
【解析】
【分析】
根据正弦定理辨析即可.
【详解】
对于A,由可得,,不一定成立,故A错误;
对于B,由可得,,不一定成立,故B错误;
对于C,由可得,,即,不一定成立,故C错误;
对于D,由正弦定理可得,,即一定成立,故D正确.
故选:D.
7.C
【解析】
【分析】
根据平均数公式计算可得;
【详解】
解:因为一组数据的平均数是1,所以
即,所以,即一组数据的平均数为;
故选:C
8.D
【解析】
【分析】
先求出直线与圆的直角坐标方程,求出半径和弦心距,再利用弦长公式求得弦长.
【详解】
直线参数方程是(为参数),
化为直角坐标方程为,
圆极坐标方程是,
化为直角坐标方程为,
即,表示以为圆心,半径,
弦心距,
弦长为.
故选:D
【点睛】
本题主要考查了参数方程与直角坐标方程的互化、极坐标方程与直角坐标方程的互化以及直线与圆相交弦长的几何求法,属于基础题.
9.D
【解析】
【分析】
根据题意得到直线与直线和直线分别平行时或直线过直线和直线的交点时,三条直线不能构成三角形,再分别计算相应的值即可.
【详解】
由题知:
①当直线与直线平行时,三条直线不能构成三角形.
即.
②当直线与直线平行时,三条直线不能构成三角形.
即.
③当直线过直线与直线交点时,
三条直线不能构成三角形.
所以,解得,
将代入,解得.
所以实数的取值集合为.
故选:D.
10.B
【解析】
【详解】
分析:圆上任意一点关于某直线的对称点还在圆上,说明该直线必过圆心,
根据圆心表达式求出圆心坐标,代入直线方程,即可求得m.
详解:由题意知,直线必过圆心,由圆心表达式可得圆心坐标为,
代入直线,解得.故选B.
点睛:圆的一般方程中,圆心坐标为,
圆的对称轴为过圆心的任意直线,可知直线过圆心.
11.D
【解析】
【详解】
由分层抽样的办法可知在名学生中抽取的男生有,故女生人数为,应选答案D.
12.B
【解析】
建立平面直角坐标系,设,利用坐标法将用点坐标表示,即可求出的最小值.
【详解】
以点为坐标原点,所在直线为轴,所在直线为轴,建立如图所示的平面直角坐标系,
设,,则,,,半圆的方程为,
所以,,,
因为,即,
所以,即,
所以,又是半圆上的任意一点,
所以,,,
所以,所以当时,取得最小值.
故选:B
【点睛】
关键点点睛:本题主要考查二元变量的最值求法,关键是根据已知把几何图形放在适当的坐标系中,把有关点与向量用坐标表示,这样就能进行相应的代数运算和向量运算,从而使问题得到解决.
13.
【解析】
【分析】
由频率分布直方图得每天在校平均开销在元的学生的频率为,由此能求出每天在校平均开销在元的学生人数.
【详解】
解:由频率分布直方图得:
每天在校平均开销在元的学生的频率为:
,
每天在校平均开销在元的学生人数为:
.
故答案为330.
【点睛】
本题考查频数的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.
14.;
【解析】
【分析】
先用诱导公式转化
得到,再用平关系求解.
【详解】
因为
所以
所以.
故答案为:.
【点睛】
本题主要考查了诱导公式和同角三角函数基本关系式,还考查了转化化归的思想和运算求解的能力,属于基础题.
15.5
【解析】
【分析】
整理,则,进而求解.
【详解】
由题,,
所以,解得,
所以,
故答案为:5
【点睛】
本题考查平面向量加法的坐标运算,属于基础题.
16.或
【解析】
分类讨论:截距等于或截距不等于,设出截距式,将点代入即可求解.
【详解】
当直线的截距等于时,即直线过,
所以直线的斜率,
所以直线方程为:,即;
当直线的截距不等于时, 设直线为,
将点P(1,-2)代入方程可得,所以,
所以直线方程为,即.
故答案为:或
【点睛】
本题考查了直线的截距式方程,考查了基本运算能力以及分类讨论的思想,属于基础题.
17.(1);(2)
【解析】
(1)首先利用三角恒等变换将函数化简,再结合,代入计算可得;
(2)根据三角函数的变换规则得到,再根据的取值范围,得到的取值范围,结合正弦函数的性质计算可得;
【详解】
解:
即
(1)
所以
所以或,
解得或,
因为为锐角,所以
(2)将各点的横坐标变为原来的2倍( 纵坐标不变)得到,再将的图象向右平移个单位得到,即
因为,所以
所以当,即时函数取得最小值
【点睛】
本题考查三角恒等变换与三角函数的性质的综合应用,考查三角函数的变换,属于中档题.
18.(I)船的行驶速度为(海里/小时).(II)船会进入警戒水域.
【解析】
【详解】
试题分析:(I)根据同角三角函数的基本关系式求出,然后利用余弦定理求出BC的值,从而可求出船的行驶速度.
(II)判断船是否会进入警戒水域,关键是看点E到直线l的距离与半径7的关系,因而可求出直线l的方程,以及E点坐标,然后再根据点到直线的距离公式得到结论.
(I)如图,AB=40,AC=10,
由于,所以cos=
由余弦定理得BC=
所以船的行驶速度为(海里/小时).
(II)解法一 如图所示,以A为原点建立平面直角坐标系,
设点B、C的坐标分别是B(x1,y2), C(x1,y2),
BC与x轴的交点为D.
由题设有,x1=y1=AB=40,
x2=ACcos,
y2=ACsin
所以过点B、C的直线l的斜率k=,直线l的方程为y=2x-40.
又点E(0,-55)到直线l的距离d=
所以船会进入警戒水域.
解法二: 如图所示,设直线AE与BC的延长线相交于点Q.
在△ABC中,由余弦定理得,
==.
从而
在中,由正弦定理得,AQ=
由于AE=55>40=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.
过点E作EPBC于点P,则EP为点E到直线BC的距离.
在Rt中,PE=QE·sin
=所以船会进入警戒水域.
考点:正余弦定理在解三角形当中的应用,直线方程,点到直线的距离,直线与圆的位置关系.
点评:掌握正余弦定理及能解决的三角形类型是解三角形的前提.第(II)问关键是知道如何判断船是否会进入警戒水域,实质是直线与圆的位置关系的判断.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)由l的方程得,根据m∈R可得定点,再根据求出|AC|与半径比较大小可得答案;
(2)由题意可知弦长最小时 ,求出,由点斜式方程可得答案.
(1)
证明:
由l的方程为,
所以解得,
即l恒过定点,
因为圆心为,所以(半径),所以点A在圆C内,从而直线l与圆C恒交于两点.
(2)
由题意可知弦长最小时 ,
因为,所以l的斜率为2,又l过点,由点斜式方程可得l的方程为.
20.(1) ;(2).
【解析】
【详解】
试题分析:(1)化简.由当时,取最大值当时,取最小值值域为;(2)由
.
试题解析:.
(1),∴,
则当,即时,取最大值,即有,得.
∴,则当,即时,取最小值.
∴值域为.
(2),
∴,
,∴,
∴.
考点:1、三角函数的图象与性质;2、三角恒等变换.
21.(1);(2)众数为3000,中位数为;(3)
【解析】
(1)根据概率和为1计算得到答案.
(2)计算众数和中位数得到答案.
(3)直接根据概率分布直方图得到答案.
【详解】
(1)依题意,,解得.
(2)由图可知,地区200家实体店该品牌洗衣机的月经济损失的众数为3000,
第一块小矩形的面积,第二块小矩形的面积,
故所求中位数在之间,所求中位数为.
(3)直接根据概率分布直方图得到:.
【点睛】
本题考查频率分布直方图、样本的数字特征,考查运算求解能力以及必然与或然思想.
22.(1).
(2)证明见解析;定点或.
【解析】
【分析】
(1)由已知中直线过点,我们可以设出直线的点斜式方程,化为一般式方程后,代入点到直线距离公式,根据直线与圆相切,圆心到直线的距离等于半径,可以求出k的值,进而得到直线的方程;
(2)由已知我们易求出P,Q两个点的坐标,设出M点的坐标,我们可以得到点P与Q的坐标,进而得到以为直径的圆的方程,根据圆的方程即可判断结论.
【详解】
(Ⅰ)由题意得,直线的斜率存在.
设直线的方程为.
因为直线与圆相切,
所以.
所以.
所以直线方程为.
(Ⅱ)由题意得,点,点.
设点,则.
直线的方程为.
所以直线与直线的交点为点.
直线的方程为.
所以直线与直线的交点为点.
设点.
则,.
因为以为直径的圆与轴交于定点,
所以
解得.
所以定点或.
【点睛】
该题考查的是有关直线与圆的方程的应用问题,涉及到的知识点有过圆外一点圆的切线方程的求法,圆与直线的交点,直线方程的点斜式,圆的方程的问题,直径所对的圆周角为直角,垂直应用向量的数量积等于零等,认真分析题意,求得结果.
试卷第页,共页
试卷第页,共页
同课章节目录
