2021-2022学年人教版八年级下册数学 17.1勾股定理 同步习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级下册数学 17.1勾股定理 同步习题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 14:24:34 | ||
图片预览



文档简介
17.1勾股定理 同步习题
一.选择题
1.直角三角形的两条边长为5和12,它的斜边长为( )
A.13 B. C.13或 D.13或12
2.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3 B.6 C.8 D.5
3.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB,则CD等于( )
A.4.8 B.14 C.10 D.2.4
4.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
5.如图,以数轴的单位长线段为边做一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
A.1 B.1.4 C. D.
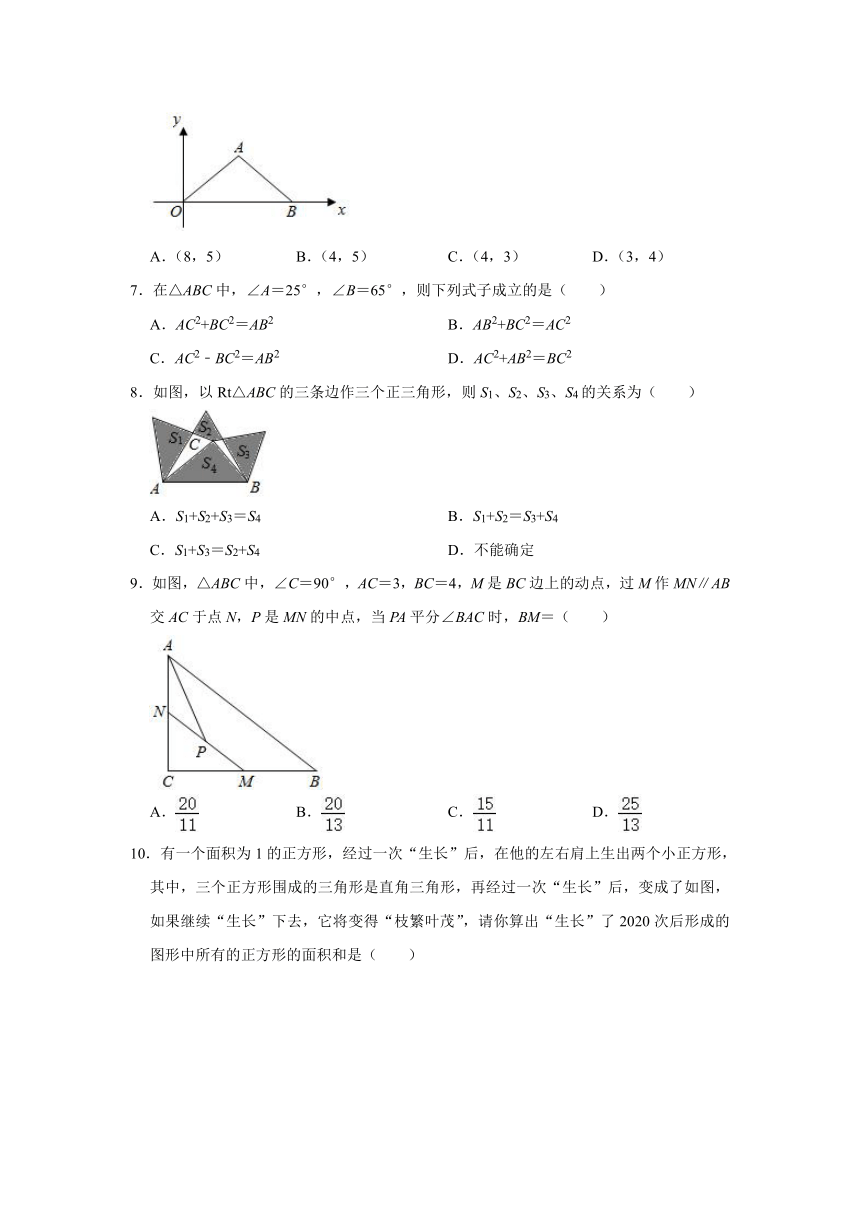
6.如图,平面直角坐标系中,△OAB的边OB落在x轴上,顶点A落在第一象限.若OA=AB=5,OB=8,则点A的坐标是( )
A.(8,5) B.(4,5) C.(4,3) D.(3,4)
7.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+BC2=AB2 B.AB2+BC2=AC2
C.AC2﹣BC2=AB2 D.AC2+AB2=BC2
8.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为( )
A.S1+S2+S3=S4 B.S1+S2=S3+S4
C.S1+S3=S2+S4 D.不能确定
9.如图,△ABC中,∠C=90°,AC=3,BC=4,M是BC边上的动点,过M作MN∥AB交AC于点N,P是MN的中点,当PA平分∠BAC时,BM=( )
A. B. C. D.
10.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是( )
A.1 B.2021 C.2020 D.2019
二.填空题
11.已知一个直角三角形的两边长分别为3和4,则这个三角形斜边上的高为 .
12.如图所示,Rt△ABC中,∠ACB=90°,AC=4,BC=3,E为斜边AB上一点,连接CE,若CE=,则线段AE的长为 .
13.在Rt△ABC中,斜边AB=3,则AB2+BC2+CA2= .
14.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为 .
15.如图,在Rt△ABC中,∠C=90°,BE,AF分别是∠ABC,∠ACB平分线,BE,AF交于点O,OM⊥AB,AB=10,AC=8,则OM= .
三.解答题
16.如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=12,BD=5.
(1)求证:△BDC是直角三角形;
(2)求AC的长.
17.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒2cm的速度沿折线A→C→B→A运动,设运动时间为t(t>0)秒
(1)若点P恰好在∠BAC的平分线上,求t的值;
(2)若△CBP为等腰三角形,求t的值;
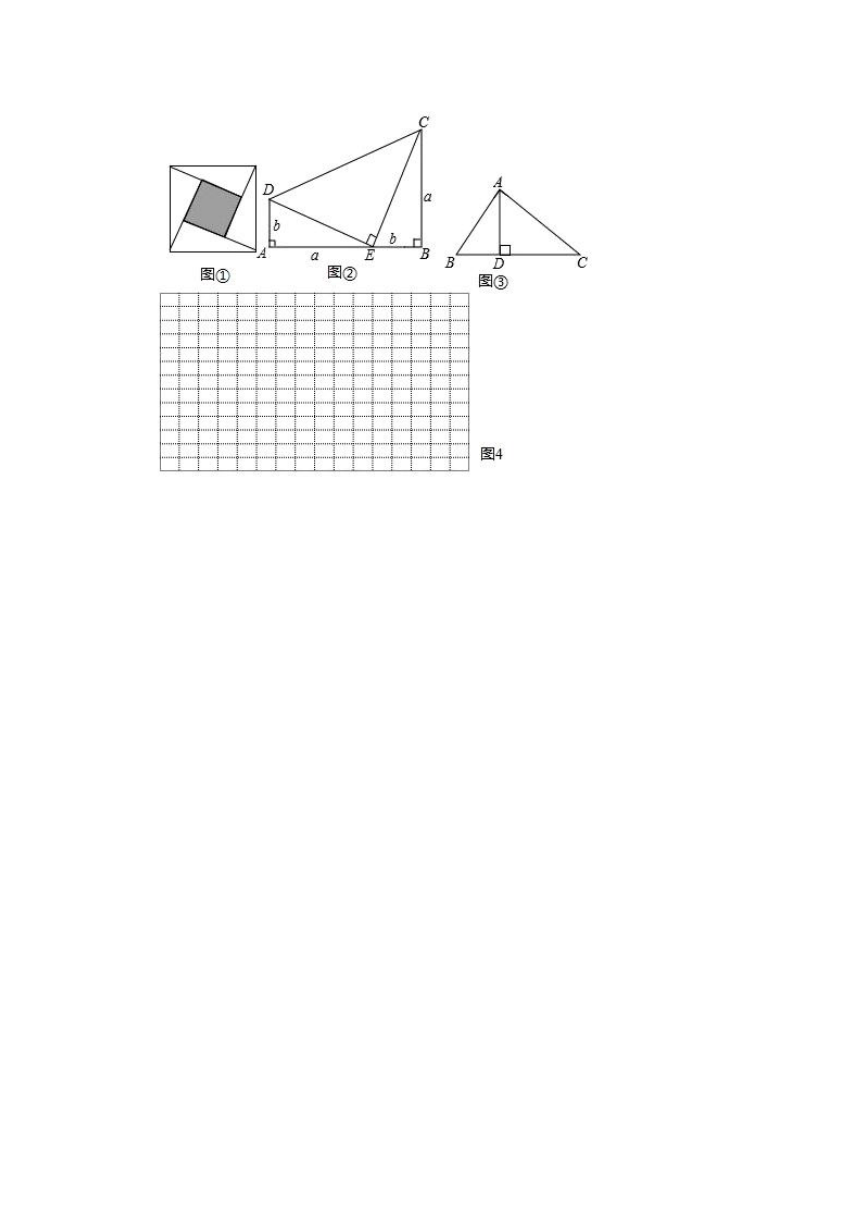
18.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4×ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在如图4的网格中,并标出字母a,b所表示的线段.
参考答案
一.选择题
1.解:当12是直角边时,斜边长==13.
故它的斜边长为13或12.
故选:D.
2.解:设两直角边分别为3x,4x.
由勾股定理得(3x)2+(4x)2=100.
解得x=2.则3x=3×2=6,4x=4×2=8.
∴直角三角形的两直角边的长分别为6,8.
较短直角边的长为6.
故选:B.
3.解:∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∴AC BC=AB CD,即6×8=10×CD,
解得,CD=4.8,
故选:A.
4.解:由勾股定理得,AB2+BC2=AC2,
则S=25+400=625,
故选:D.
5.解:由勾股定理得,OB==,
则OA=OB=,
∴点A表示的数是,
故选:C.
6.解:如图,过点A作AD⊥OB于点D,
∵OA=AB=5,OB=8,
∴OD=OB=4.
在直角△OAD中,由勾股定理得:AD===3.
故点A的坐标是(4,3).
故选:C.
7.解:∵在△ABC中,∠A=25°,∠B=65°,
∴∠C=180°﹣∠A﹣∠B=90°,
∴△ABC是直角三角形,
∴AC2+BC2=AB2,故选项A正确,选项B、C、D错误,
故选:A.
8.解:如图,设Rt△ABC的三条边AB=c,AC=b,BC=a,
∵△ACG,△BCH,△ABF是等边三角形,
∴S1=S△ACG﹣S5=b2﹣S5,S3=S△BCH﹣S6=a2﹣S6,
∴S1+S3=(a2+b2)﹣S5﹣S6,
∵S2+S4=S△ABF﹣S5﹣S6=c2﹣S5﹣S6,
∵c2=a2+b2,
∴S1+S3=S2+S4,
故选:C.
9.解:作PD⊥AC于D,PE⊥AB于E,MF⊥AB于F,
由勾股定理得,AB==5,
∵PA平分∠BAC,PD⊥AC,PE⊥AB,
∴PD=PE,
∵PE⊥AB,MF⊥AB,MN∥AB,
∴四边形PMFE为矩形,
∴PE=MF,
设PD=PE=MF=3x,
∵∠B=∠B,∠BFM=∠BCA,
∴△BMF∽△BAC,
∴=,即=,
解得,BM=5x,
∵PD∥BC,P是MN的中点,
∴BC=6x+5x=11x,
由题意得,11x=4,
解得,x=,
∴BM=5x=,
故选:A.
10.解:由题意得,正方形A的面积为1,
由勾股定理得,正方形B的面积+正方形C的面积=1,
∴“生长”了1次后形成的图形中所有的正方形的面积和为2,
同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为3,
∴“生长”了3次后形成的图形中所有的正方形的面积和为4,
……
∴“生长”了2020次后形成的图形中所有的正方形的面积和为2021,
故选:B.
二.填空题
11.解:分为两种情况:
①斜边是4有一条直角边是3,
由勾股定理得:第三边长==,
∴斜边上的高为=;
②3和4都是直角边,
由勾股定理得:第三边长==5,
∴斜边上的高为=;
故答案为:或.
12.解:∵∠ACB=90°,AC=4,BC=3,
∴AB==5,
过C作CD⊥AB于D,
∴∠CDA=∠CDB=90°,CD===,
∴AD==,
∵CE=,
∴DE==1,
∴AE=AD﹣DE=或AE=AD+DE=,
故答案为:或.
13.解:∵△ABC为直角三角形,AB为斜边,
∴AC2+BC2=AB2,又AB=3,
∴AC2+BC2=AB2=9,
则AB2+BC2+CA2=AB2+(BC2+CA2)=9+9=18.
故答案为:18
14.解:由勾股定理得:AC=,
∵S△ABC=3×3﹣,
∴,
∴,
∴BD=,
故答案为:.
15.解:过O作OG⊥AC于G,OH⊥BC于H,连接OC,
∵AF平分∠CAB,BE平分∠ABC,
∴OG=OH=OM,
∵∠C=90°,AB=10,AC=8,
∴BC==6
∴S△ABC=AC BC=×AB OM+AC OG+BC OH,
∴×8×6=+×8×OG+,
∴OM=2,
故答案为:2.
三.解答题
16.证明:(1)∵BC=13,CD=12,BD=5,
∴BC2=BD2+CD2,
∴△BDC为直角三角形;
(2)设AB=x,
∵△ABC是等腰三角形,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2=(x﹣5)2+122,
解得:x=16.9,
∴AC=16.9.
17.解:(1)∵△ABC中,∠C=90°,AB=10cm,BC=6cm,
∴AC==8(cm),
当点P在∠BAC的平分线上时,如图1,过点P作PE⊥AB于点E,
此时BP=(14﹣2t)cm,PE=PC=(2t﹣8)cm,BE=10﹣8=2(cm),
在Rt△BEP中,PE2+BE2=BP2,
即:(2t﹣8)2+22=(14﹣2t)2,
解得:t=,
当t=12秒时,点P与A重合,也符合条件,
∴当t=或12时,点P恰好在∠BAC的平分线上;
(2)根据题意得:AP=2tcm,
当P在AC上时,△BCP为等腰三角形,
∴PC=BC,即8﹣2t=6,
∴t=1,
当P在AB上时,△BCP为等腰三角形,
①CP=PB,点P在BC的垂直平分线上,
如图2,过P作PE⊥BC于E,
∴BE=BC=3cm,
∴PB=AB,即2t﹣6﹣8=5,解得:t=,
②PB=BC,即2t﹣6﹣8=6,
解得:t=10,
③PC=BC,如图3,过C作CF⊥AB于F,
∴BF=BP,
∵∠ACB=90°,
依题意有CF=8×6÷10=(cm),
在Rt△BFC中,BF==(cm),
∴PB=2BF=(cm),
∴t=(8+6+)÷2=,
∴当t=1或或10或时,△BCP为等腰三角形.
18.解:(1)梯形ABCD的面积为,
也可以表示为,∴,
即a2+b2=c2;
(2)在Rt△ABD中,AD2=AB2﹣BD2=42﹣x2=16﹣x2;
在Rt△ADC中,AD2=AC2﹣DC2=52﹣(6﹣x)2=﹣11+12x﹣x2;
所以16﹣x2=﹣11+12x﹣x2,
解得;
(3)如图,
由此可得(a+b)(a+2b)=a2+3ab+2b2.
一.选择题
1.直角三角形的两条边长为5和12,它的斜边长为( )
A.13 B. C.13或 D.13或12
2.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3 B.6 C.8 D.5
3.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD⊥AB,则CD等于( )
A.4.8 B.14 C.10 D.2.4
4.如图所示,在△ABC中,∠ABC=90°,分别以AB、BC、AC为边向外作正方形,面积分别为225、400、S,则S为( )
A.175 B.600 C.25 D.625
5.如图,以数轴的单位长线段为边做一个正方形,数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( )
A.1 B.1.4 C. D.
6.如图,平面直角坐标系中,△OAB的边OB落在x轴上,顶点A落在第一象限.若OA=AB=5,OB=8,则点A的坐标是( )
A.(8,5) B.(4,5) C.(4,3) D.(3,4)
7.在△ABC中,∠A=25°,∠B=65°,则下列式子成立的是( )
A.AC2+BC2=AB2 B.AB2+BC2=AC2
C.AC2﹣BC2=AB2 D.AC2+AB2=BC2
8.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为( )
A.S1+S2+S3=S4 B.S1+S2=S3+S4
C.S1+S3=S2+S4 D.不能确定
9.如图,△ABC中,∠C=90°,AC=3,BC=4,M是BC边上的动点,过M作MN∥AB交AC于点N,P是MN的中点,当PA平分∠BAC时,BM=( )
A. B. C. D.
10.有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2020次后形成的图形中所有的正方形的面积和是( )
A.1 B.2021 C.2020 D.2019
二.填空题
11.已知一个直角三角形的两边长分别为3和4,则这个三角形斜边上的高为 .
12.如图所示,Rt△ABC中,∠ACB=90°,AC=4,BC=3,E为斜边AB上一点,连接CE,若CE=,则线段AE的长为 .
13.在Rt△ABC中,斜边AB=3,则AB2+BC2+CA2= .
14.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为 .
15.如图,在Rt△ABC中,∠C=90°,BE,AF分别是∠ABC,∠ACB平分线,BE,AF交于点O,OM⊥AB,AB=10,AC=8,则OM= .
三.解答题
16.如图,已知等腰△ABC的底边BC=13,D是腰AB上一点,且CD=12,BD=5.
(1)求证:△BDC是直角三角形;
(2)求AC的长.
17.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒2cm的速度沿折线A→C→B→A运动,设运动时间为t(t>0)秒
(1)若点P恰好在∠BAC的平分线上,求t的值;
(2)若△CBP为等腰三角形,求t的值;
18.教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c),也可以表示为4×ab+(a﹣b)2,由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2.
(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2,画在如图4的网格中,并标出字母a,b所表示的线段.
参考答案
一.选择题
1.解:当12是直角边时,斜边长==13.
故它的斜边长为13或12.
故选:D.
2.解:设两直角边分别为3x,4x.
由勾股定理得(3x)2+(4x)2=100.
解得x=2.则3x=3×2=6,4x=4×2=8.
∴直角三角形的两直角边的长分别为6,8.
较短直角边的长为6.
故选:B.
3.解:∵∠ACB=90°,AC=6,BC=8,
∴AB===10,
∴AC BC=AB CD,即6×8=10×CD,
解得,CD=4.8,
故选:A.
4.解:由勾股定理得,AB2+BC2=AC2,
则S=25+400=625,
故选:D.
5.解:由勾股定理得,OB==,
则OA=OB=,
∴点A表示的数是,
故选:C.
6.解:如图,过点A作AD⊥OB于点D,
∵OA=AB=5,OB=8,
∴OD=OB=4.
在直角△OAD中,由勾股定理得:AD===3.
故点A的坐标是(4,3).
故选:C.
7.解:∵在△ABC中,∠A=25°,∠B=65°,
∴∠C=180°﹣∠A﹣∠B=90°,
∴△ABC是直角三角形,
∴AC2+BC2=AB2,故选项A正确,选项B、C、D错误,
故选:A.
8.解:如图,设Rt△ABC的三条边AB=c,AC=b,BC=a,
∵△ACG,△BCH,△ABF是等边三角形,
∴S1=S△ACG﹣S5=b2﹣S5,S3=S△BCH﹣S6=a2﹣S6,
∴S1+S3=(a2+b2)﹣S5﹣S6,
∵S2+S4=S△ABF﹣S5﹣S6=c2﹣S5﹣S6,
∵c2=a2+b2,
∴S1+S3=S2+S4,
故选:C.
9.解:作PD⊥AC于D,PE⊥AB于E,MF⊥AB于F,
由勾股定理得,AB==5,
∵PA平分∠BAC,PD⊥AC,PE⊥AB,
∴PD=PE,
∵PE⊥AB,MF⊥AB,MN∥AB,
∴四边形PMFE为矩形,
∴PE=MF,
设PD=PE=MF=3x,
∵∠B=∠B,∠BFM=∠BCA,
∴△BMF∽△BAC,
∴=,即=,
解得,BM=5x,
∵PD∥BC,P是MN的中点,
∴BC=6x+5x=11x,
由题意得,11x=4,
解得,x=,
∴BM=5x=,
故选:A.
10.解:由题意得,正方形A的面积为1,
由勾股定理得,正方形B的面积+正方形C的面积=1,
∴“生长”了1次后形成的图形中所有的正方形的面积和为2,
同理可得,“生长”了2次后形成的图形中所有的正方形的面积和为3,
∴“生长”了3次后形成的图形中所有的正方形的面积和为4,
……
∴“生长”了2020次后形成的图形中所有的正方形的面积和为2021,
故选:B.
二.填空题
11.解:分为两种情况:
①斜边是4有一条直角边是3,
由勾股定理得:第三边长==,
∴斜边上的高为=;
②3和4都是直角边,
由勾股定理得:第三边长==5,
∴斜边上的高为=;
故答案为:或.
12.解:∵∠ACB=90°,AC=4,BC=3,
∴AB==5,
过C作CD⊥AB于D,
∴∠CDA=∠CDB=90°,CD===,
∴AD==,
∵CE=,
∴DE==1,
∴AE=AD﹣DE=或AE=AD+DE=,
故答案为:或.
13.解:∵△ABC为直角三角形,AB为斜边,
∴AC2+BC2=AB2,又AB=3,
∴AC2+BC2=AB2=9,
则AB2+BC2+CA2=AB2+(BC2+CA2)=9+9=18.
故答案为:18
14.解:由勾股定理得:AC=,
∵S△ABC=3×3﹣,
∴,
∴,
∴BD=,
故答案为:.
15.解:过O作OG⊥AC于G,OH⊥BC于H,连接OC,
∵AF平分∠CAB,BE平分∠ABC,
∴OG=OH=OM,
∵∠C=90°,AB=10,AC=8,
∴BC==6
∴S△ABC=AC BC=×AB OM+AC OG+BC OH,
∴×8×6=+×8×OG+,
∴OM=2,
故答案为:2.
三.解答题
16.证明:(1)∵BC=13,CD=12,BD=5,
∴BC2=BD2+CD2,
∴△BDC为直角三角形;
(2)设AB=x,
∵△ABC是等腰三角形,
∴AB=AC=x,
∵AC2=AD2+CD2,
即x2=(x﹣5)2+122,
解得:x=16.9,
∴AC=16.9.
17.解:(1)∵△ABC中,∠C=90°,AB=10cm,BC=6cm,
∴AC==8(cm),
当点P在∠BAC的平分线上时,如图1,过点P作PE⊥AB于点E,
此时BP=(14﹣2t)cm,PE=PC=(2t﹣8)cm,BE=10﹣8=2(cm),
在Rt△BEP中,PE2+BE2=BP2,
即:(2t﹣8)2+22=(14﹣2t)2,
解得:t=,
当t=12秒时,点P与A重合,也符合条件,
∴当t=或12时,点P恰好在∠BAC的平分线上;
(2)根据题意得:AP=2tcm,
当P在AC上时,△BCP为等腰三角形,
∴PC=BC,即8﹣2t=6,
∴t=1,
当P在AB上时,△BCP为等腰三角形,
①CP=PB,点P在BC的垂直平分线上,
如图2,过P作PE⊥BC于E,
∴BE=BC=3cm,
∴PB=AB,即2t﹣6﹣8=5,解得:t=,
②PB=BC,即2t﹣6﹣8=6,
解得:t=10,
③PC=BC,如图3,过C作CF⊥AB于F,
∴BF=BP,
∵∠ACB=90°,
依题意有CF=8×6÷10=(cm),
在Rt△BFC中,BF==(cm),
∴PB=2BF=(cm),
∴t=(8+6+)÷2=,
∴当t=1或或10或时,△BCP为等腰三角形.
18.解:(1)梯形ABCD的面积为,
也可以表示为,∴,
即a2+b2=c2;
(2)在Rt△ABD中,AD2=AB2﹣BD2=42﹣x2=16﹣x2;
在Rt△ADC中,AD2=AC2﹣DC2=52﹣(6﹣x)2=﹣11+12x﹣x2;
所以16﹣x2=﹣11+12x﹣x2,
解得;
(3)如图,
由此可得(a+b)(a+2b)=a2+3ab+2b2.
