人教版数学七年级下册 第17章 17.1 勾股定理同步测试试题(一)(word版含答案)
文档属性
| 名称 | 人教版数学七年级下册 第17章 17.1 勾股定理同步测试试题(一)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 13:52:02 | ||
图片预览


文档简介
勾股定理同步测试试题(一)
一.选择题
1.如图,在行距、列距都是1的4×4的方格网中,将任意连接两个格点的线段称作“格点线”,则“格点线”的长度不可能等于( )
A. B. C. D.
2.已知直角三角形的两边长分别为3和4,则斜边长为( )
A.4 B.5 C.4或5 D.5或
3.在Rt△ABC中,∠C=90°,BC=2,AB=3,则边AC的长为( )
A.5 B. C. D.1
4.若直角三角形的两条边的长分别为和2,则该直角三角形第三边的长为( )
A.1 B. C.5 D.1或
5.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
6.如图,在三角形ABC中,已知∠C=90°,AC=3,BC=4,则AB的大小有可能是( )
A.1 B.2 C.3 D.5
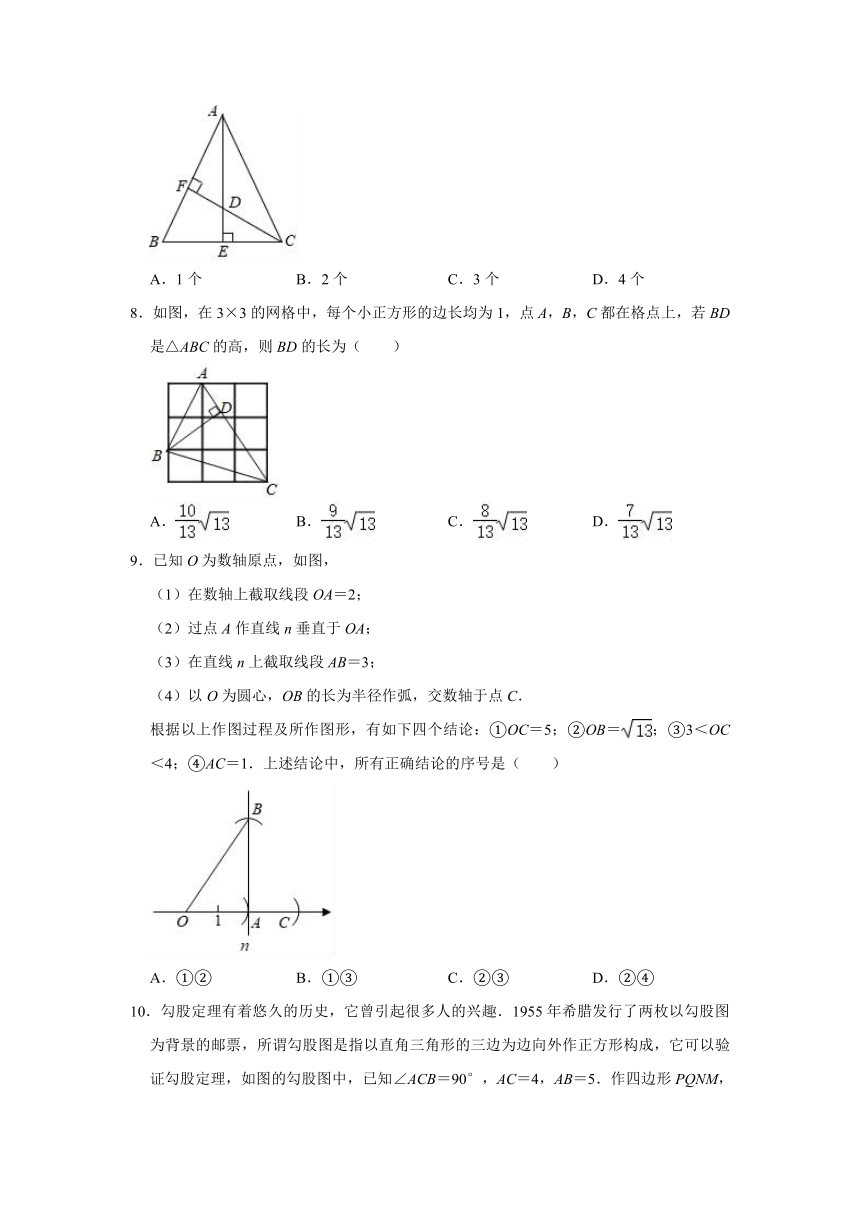
7.如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
8.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
9.已知O为数轴原点,如图,
(1)在数轴上截取线段OA=2;
(2)过点A作直线n垂直于OA;
(3)在直线n上截取线段AB=3;
(4)以O为圆心,OB的长为半径作弧,交数轴于点C.
根据以上作图过程及所作图形,有如下四个结论:①OC=5;②OB=;③3<OC<4;④AC=1.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.②④
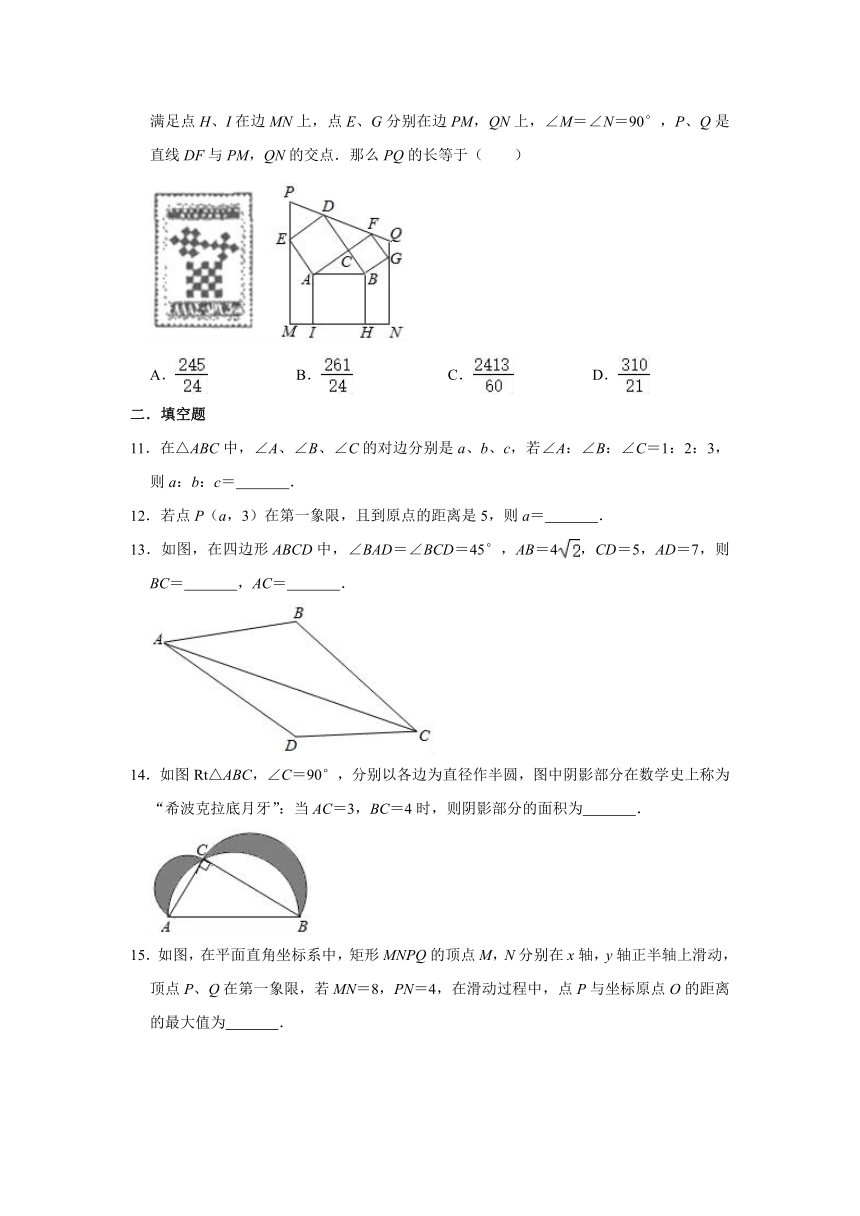
10.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票,所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理,如图的勾股图中,已知∠ACB=90°,AC=4,AB=5.作四边形PQNM,满足点H、I在边MN上,点E、G分别在边PM,QN上,∠M=∠N=90°,P、Q是直线DF与PM,QN的交点.那么PQ的长等于( )
A. B. C. D.
二.填空题
11.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若∠A:∠B:∠C=1:2:3,则a:b:c= .
12.若点P(a,3)在第一象限,且到原点的距离是5,则a= .
13.如图,在四边形ABCD中,∠BAD=∠BCD=45°,AB=4,CD=5,AD=7,则BC= ,AC= .
14.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .
15.如图,在平面直角坐标系中,矩形MNPQ的顶点M,N分别在x轴,y轴正半轴上滑动,顶点P、Q在第一象限,若MN=8,PN=4,在滑动过程中,点P与坐标原点O的距离的最大值为 .
三.解答题
16.我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
以a、b 为直角边,以c为斜边作两个全等的直角三角形,把这两个直角三角形拼成如图所示梯形形状,使C、B、D三点在一条直线上.
你能利用该图证明勾股定理吗?写出你的证明过程.
17.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.
18.如图所示网格是由边长为1的小正方形组成,点A,B,C位置如图所示,在网格中确定点D,使以A,B,C,D为顶点的四边形的所有内角都相等.
(1)确定点D的位置并画出以A,B,C,D为顶点的四边形;
(2)直接写出(1)中所画出的四边形的周长和面积.
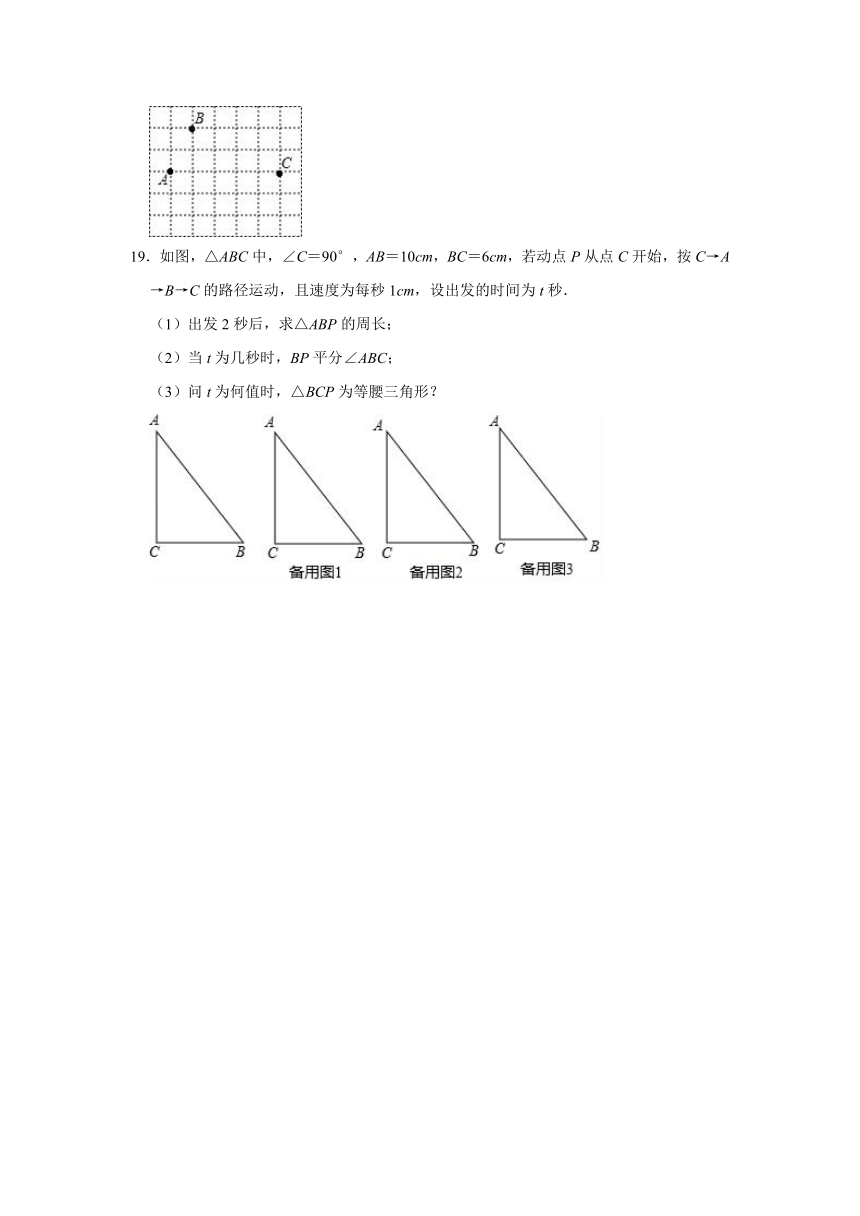
19.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
参考答案与试题解析
一.选择题
1.【解答】解:∵=,故可能是“格点线”的长度,故选项A不符合题意;
∵,故可能是“格点线”的长度,故选项B不符合题意;
∵,故不可能是“格点线”的长度,故选项C符合题意;
∵,故可能是“格点线”的长度,故选项D不符合题意;
故选:C.
2.【解答】解:∵直角三角形的两边长分别为3和4,
∴①4是此直角三角形的斜边长;
②当4是此直角三角形的直角边长时,斜边长为=5.
综上所述,斜边长为4或5.
故选:C.
3.【解答】解:∵在Rt△ABC中,∠C=90°,BC=2,AB=3,
∴AC===.
故选:C.
4.【解答】解:当2是斜边长时,由勾股定理得,另一条直角边==1,
当2是直角边时,由勾股定理得,斜边长==,
∴该直角三角形第三边的长为1或,
故选:D.
5.【解答】解:∵一个三角形一条直角边长是3,另一条直角边长是4,
∴斜边长==5.
故选:A.
6.【解答】解:方法1:由垂线段最短,可得AB的大小有可能是5.
方法2:在三角形ABC中,∠C=90°,AC=3,BC=4,
则AB===5.
故选:D.
7.【解答】解:①∵在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,
∴AE⊥BC,BE=CE=4cm,
在Rt△DEC中,CD==5cm,故①正确;
②∵∠ACD=∠CAD,
∴AD=CD=5cm,
∴AE=8cm,
在Rt△AEC中,AC==4cm,故②错误;
③∵∠DAF=∠BAE,∠AFD=∠AEB,
∴△DAF∽△BAE,
∴DF:AD=BE:AB,即DF:5=4:4,
解得DF=.
故DF=cm,故③错误;
④△ACD的面积为5×4÷2=10cm2,故④正确.
故选:B.
8.【解答】解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
9.【解答】解:根据题意得,OA=2,AB=3,∠OAB=90°,
∴OB=,
故②正确;
∵OC=OB,
∴OC=,
∴③正确,①错误;
∴AC=OC﹣OA=﹣2≠1,
故④错误;
故选:C.
10.【解答】解:如图,延长FA交PM于J,过点P作PK⊥DE于K,过点Q作QW⊥FG于W.
∵四边形ACDE,四边形BCFG都是正方形,
∴∠ACD=∠BCF=90°,AC=CD,BC=CF,
∵CA=CD,CB=CF,∠ACB=∠DCF=90°,
∴△DCF≌△ACB(SAS),
∴∠DFC=∠ABC,DF=AB=5,
∵AC=4,
∴BC===3,
∵PM∥AI,DE∥AF,
∴∠PDE=∠PFJ,∠PED=∠PJF=∠JAI,
∵∠JAI+∠BAC=90°,∠BAC+∠ABC=90°,
∴∠JAI=∠ABC,
∴∠PJF=∠PFJ,
∴∠PED=∠PDE,
∴PD=PE,
∵PK⊥DE,
∴EK=DK=2,
∵∠PKD=∠DCF=90°,∠PDK=∠DFC,
∴△PKD∽△DCF,
∴=,
∴=,
∴PD=,
同法可证,FW=WG=1.5,△QFW∽△FDC,
∴=,
∴=,
∴QF=,
∴PQ=PD+DF+FQ=+5+=,
故选:A.
二.填空题(共5小题)
11.【解答】解:∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°,
∵在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,
∴c=2a,b===a,
∴a:b:c=a: a:2a=1::2,
故答案为:1::2.
12.【解答】解:∵点P(a,3)到原点的距离是5,
∴a2+32=52.
∴a=±4.
∵点P(a,3)在第一象限,
∴a=4.
故答案为:4.
13.【解答】解:过B作BE⊥AD于E,过C作CF⊥AD交AD的延长线于F,
连接BD,
则∠BEA=∠BED=∠CFD=90°,
∵AB=4,∠BAD=45°,
∴AE=BE=4,
∵AD=7,
∴DE=3,
∴BD===5,
∵CD=5,
∴BD=CD,
∵∠BCD=45°,
∴DBC=∠BCD=45°,
∴∠BDC=90°,
∴BC=CD=5,
∵∠EBD+∠BDE=∠BDE+∠CDF=90°,
∴∠EBD=∠CDF,
∵∠BED=∠CFD=90°,BD=CD,
∴△BDE≌△DCF(AAS),
∴DF=BE=4,CF=DE=3,
∴AF=11,
∴AC===.
故答案为:5,.
14.【解答】解:在Rt△ACB中,∠ACB=90°,AC=3,BC=4,由勾股定理得:AB===5,
所以阴影部分的面积S=×π×()2+π×()2+﹣π×()2=6,
故答案是:6.
15.【解答】解:如图,取MN的中点E,连接OE,PE,OP,
∵∠MON=90°,
∴Rt△MON中,OE=MN=4,
又∵∠MQP=90°,MN=8,PN=4,NE=4,
∴Rt△PNE中,PE=,
又∵OP≤PE+OE=4+4,
∴OP的最大值为4+4,
即点P到原点O距离的最大值是4+4,
故答案为:4+4.
三.解答题(共4小题)
16.【解答】解:∵Rt△ACB≌Rt△BDE,
∴∠CAB=∠DBE.
∵∠CAB+∠ABC=90°,
∴∠ABC+∠DBE=90°.
∴∠ABE=180°﹣90o=90o.
∴△ABE是一个等腰直角三角形,S△ABE=c2.
又∵S梯形ACDE=(a+b)2,
S梯形ACDE=S△ABC+S△BDE+S△ABE=ab+c2.
∴(a+b)2=ab+c2,
即a2+b2=c2.
由此验证勾股定理.
17.【解答】解:∵大正方形的面积是13,小正方形的面积是1,
∴直角三角形的斜边的平方为13,
∵直角三角形较短的直角边为a,较长的直角边为b,
∴a2+b2=13,
∵大正方形的面积减去小正方形的面积等于四个直角三角形的面积,
∴4×ab=13﹣1,即2ab=12,
∴(a+b)2=a2+2ab+b2=13+12=25.
18.【解答】解:(1)如图所示:
(2)AB==,
BC==2,
周长为(2+)×2=6,
面积为2×=10.
19.【解答】解:(1)∵∠C=90°,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴由勾股定理得PB=2cm
∴△ABP的周长为:AP+PB+AB=6+10+2=(16+2)cm;
(2)如图2所示,过点P作PD⊥AB于点D,
∵BP平分∠ABC,
∴PD=PC.
在Rt△BPD与Rt△BPC中,,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=10﹣6=4 cm.
设PC=x cm,则PA=(8﹣x)cm
在Rt△APD中,PD2+AD2=PA2,
即x2+42=(8﹣x)2,
解得:x=3,
∴当t=3秒时,AP平分∠CAB;
(3)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形.
一.选择题
1.如图,在行距、列距都是1的4×4的方格网中,将任意连接两个格点的线段称作“格点线”,则“格点线”的长度不可能等于( )
A. B. C. D.
2.已知直角三角形的两边长分别为3和4,则斜边长为( )
A.4 B.5 C.4或5 D.5或
3.在Rt△ABC中,∠C=90°,BC=2,AB=3,则边AC的长为( )
A.5 B. C. D.1
4.若直角三角形的两条边的长分别为和2,则该直角三角形第三边的长为( )
A.1 B. C.5 D.1或
5.在一个直角三角形中,如果一条直角边长是3,另一条直角边长是4,那么斜边长是( )
A.5 B. C.5或 D.不确定
6.如图,在三角形ABC中,已知∠C=90°,AC=3,BC=4,则AB的大小有可能是( )
A.1 B.2 C.3 D.5
7.如图,在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,交BC于点E.D为AE上一点,且∠ACD=∠CAD,DE=3cm,连接CD.过点D作DF⊥AB,垂足为点F,则下列结论正确的有( )
①CD=5cm;②AC=10cm;③DF=3cm;④△ACD的面积为10cm2.
A.1个 B.2个 C.3个 D.4个
8.如图,在3×3的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,若BD是△ABC的高,则BD的长为( )
A. B. C. D.
9.已知O为数轴原点,如图,
(1)在数轴上截取线段OA=2;
(2)过点A作直线n垂直于OA;
(3)在直线n上截取线段AB=3;
(4)以O为圆心,OB的长为半径作弧,交数轴于点C.
根据以上作图过程及所作图形,有如下四个结论:①OC=5;②OB=;③3<OC<4;④AC=1.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.②③ D.②④
10.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了两枚以勾股图为背景的邮票,所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理,如图的勾股图中,已知∠ACB=90°,AC=4,AB=5.作四边形PQNM,满足点H、I在边MN上,点E、G分别在边PM,QN上,∠M=∠N=90°,P、Q是直线DF与PM,QN的交点.那么PQ的长等于( )
A. B. C. D.
二.填空题
11.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若∠A:∠B:∠C=1:2:3,则a:b:c= .
12.若点P(a,3)在第一象限,且到原点的距离是5,则a= .
13.如图,在四边形ABCD中,∠BAD=∠BCD=45°,AB=4,CD=5,AD=7,则BC= ,AC= .
14.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=3,BC=4时,则阴影部分的面积为 .
15.如图,在平面直角坐标系中,矩形MNPQ的顶点M,N分别在x轴,y轴正半轴上滑动,顶点P、Q在第一象限,若MN=8,PN=4,在滑动过程中,点P与坐标原点O的距离的最大值为 .
三.解答题
16.我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
以a、b 为直角边,以c为斜边作两个全等的直角三角形,把这两个直角三角形拼成如图所示梯形形状,使C、B、D三点在一条直线上.
你能利用该图证明勾股定理吗?写出你的证明过程.
17.如图的图形取材于我国古代数学家赵爽的《勾股圆方图》(也称《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,试求(a+b)2的值.
18.如图所示网格是由边长为1的小正方形组成,点A,B,C位置如图所示,在网格中确定点D,使以A,B,C,D为顶点的四边形的所有内角都相等.
(1)确定点D的位置并画出以A,B,C,D为顶点的四边形;
(2)直接写出(1)中所画出的四边形的周长和面积.
19.如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
参考答案与试题解析
一.选择题
1.【解答】解:∵=,故可能是“格点线”的长度,故选项A不符合题意;
∵,故可能是“格点线”的长度,故选项B不符合题意;
∵,故不可能是“格点线”的长度,故选项C符合题意;
∵,故可能是“格点线”的长度,故选项D不符合题意;
故选:C.
2.【解答】解:∵直角三角形的两边长分别为3和4,
∴①4是此直角三角形的斜边长;
②当4是此直角三角形的直角边长时,斜边长为=5.
综上所述,斜边长为4或5.
故选:C.
3.【解答】解:∵在Rt△ABC中,∠C=90°,BC=2,AB=3,
∴AC===.
故选:C.
4.【解答】解:当2是斜边长时,由勾股定理得,另一条直角边==1,
当2是直角边时,由勾股定理得,斜边长==,
∴该直角三角形第三边的长为1或,
故选:D.
5.【解答】解:∵一个三角形一条直角边长是3,另一条直角边长是4,
∴斜边长==5.
故选:A.
6.【解答】解:方法1:由垂线段最短,可得AB的大小有可能是5.
方法2:在三角形ABC中,∠C=90°,AC=3,BC=4,
则AB===5.
故选:D.
7.【解答】解:①∵在△ABC中,AB=AC,BC=8cm,AE平分∠BAC,
∴AE⊥BC,BE=CE=4cm,
在Rt△DEC中,CD==5cm,故①正确;
②∵∠ACD=∠CAD,
∴AD=CD=5cm,
∴AE=8cm,
在Rt△AEC中,AC==4cm,故②错误;
③∵∠DAF=∠BAE,∠AFD=∠AEB,
∴△DAF∽△BAE,
∴DF:AD=BE:AB,即DF:5=4:4,
解得DF=.
故DF=cm,故③错误;
④△ACD的面积为5×4÷2=10cm2,故④正确.
故选:B.
8.【解答】解:由勾股定理得:AC==,
∵S△ABC=3×3﹣=3.5,
∴,
∴,
∴BD=,
故选:D.
9.【解答】解:根据题意得,OA=2,AB=3,∠OAB=90°,
∴OB=,
故②正确;
∵OC=OB,
∴OC=,
∴③正确,①错误;
∴AC=OC﹣OA=﹣2≠1,
故④错误;
故选:C.
10.【解答】解:如图,延长FA交PM于J,过点P作PK⊥DE于K,过点Q作QW⊥FG于W.
∵四边形ACDE,四边形BCFG都是正方形,
∴∠ACD=∠BCF=90°,AC=CD,BC=CF,
∵CA=CD,CB=CF,∠ACB=∠DCF=90°,
∴△DCF≌△ACB(SAS),
∴∠DFC=∠ABC,DF=AB=5,
∵AC=4,
∴BC===3,
∵PM∥AI,DE∥AF,
∴∠PDE=∠PFJ,∠PED=∠PJF=∠JAI,
∵∠JAI+∠BAC=90°,∠BAC+∠ABC=90°,
∴∠JAI=∠ABC,
∴∠PJF=∠PFJ,
∴∠PED=∠PDE,
∴PD=PE,
∵PK⊥DE,
∴EK=DK=2,
∵∠PKD=∠DCF=90°,∠PDK=∠DFC,
∴△PKD∽△DCF,
∴=,
∴=,
∴PD=,
同法可证,FW=WG=1.5,△QFW∽△FDC,
∴=,
∴=,
∴QF=,
∴PQ=PD+DF+FQ=+5+=,
故选:A.
二.填空题(共5小题)
11.【解答】解:∵∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°,
∵在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,
∴c=2a,b===a,
∴a:b:c=a: a:2a=1::2,
故答案为:1::2.
12.【解答】解:∵点P(a,3)到原点的距离是5,
∴a2+32=52.
∴a=±4.
∵点P(a,3)在第一象限,
∴a=4.
故答案为:4.
13.【解答】解:过B作BE⊥AD于E,过C作CF⊥AD交AD的延长线于F,
连接BD,
则∠BEA=∠BED=∠CFD=90°,
∵AB=4,∠BAD=45°,
∴AE=BE=4,
∵AD=7,
∴DE=3,
∴BD===5,
∵CD=5,
∴BD=CD,
∵∠BCD=45°,
∴DBC=∠BCD=45°,
∴∠BDC=90°,
∴BC=CD=5,
∵∠EBD+∠BDE=∠BDE+∠CDF=90°,
∴∠EBD=∠CDF,
∵∠BED=∠CFD=90°,BD=CD,
∴△BDE≌△DCF(AAS),
∴DF=BE=4,CF=DE=3,
∴AF=11,
∴AC===.
故答案为:5,.
14.【解答】解:在Rt△ACB中,∠ACB=90°,AC=3,BC=4,由勾股定理得:AB===5,
所以阴影部分的面积S=×π×()2+π×()2+﹣π×()2=6,
故答案是:6.
15.【解答】解:如图,取MN的中点E,连接OE,PE,OP,
∵∠MON=90°,
∴Rt△MON中,OE=MN=4,
又∵∠MQP=90°,MN=8,PN=4,NE=4,
∴Rt△PNE中,PE=,
又∵OP≤PE+OE=4+4,
∴OP的最大值为4+4,
即点P到原点O距离的最大值是4+4,
故答案为:4+4.
三.解答题(共4小题)
16.【解答】解:∵Rt△ACB≌Rt△BDE,
∴∠CAB=∠DBE.
∵∠CAB+∠ABC=90°,
∴∠ABC+∠DBE=90°.
∴∠ABE=180°﹣90o=90o.
∴△ABE是一个等腰直角三角形,S△ABE=c2.
又∵S梯形ACDE=(a+b)2,
S梯形ACDE=S△ABC+S△BDE+S△ABE=ab+c2.
∴(a+b)2=ab+c2,
即a2+b2=c2.
由此验证勾股定理.
17.【解答】解:∵大正方形的面积是13,小正方形的面积是1,
∴直角三角形的斜边的平方为13,
∵直角三角形较短的直角边为a,较长的直角边为b,
∴a2+b2=13,
∵大正方形的面积减去小正方形的面积等于四个直角三角形的面积,
∴4×ab=13﹣1,即2ab=12,
∴(a+b)2=a2+2ab+b2=13+12=25.
18.【解答】解:(1)如图所示:
(2)AB==,
BC==2,
周长为(2+)×2=6,
面积为2×=10.
19.【解答】解:(1)∵∠C=90°,AB=10cm,BC=6cm,∴有勾股定理得AC=8cm,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm
∴出发2秒后,则CP=2cm,那么AP=6cm.
∵∠C=90°,
∴由勾股定理得PB=2cm
∴△ABP的周长为:AP+PB+AB=6+10+2=(16+2)cm;
(2)如图2所示,过点P作PD⊥AB于点D,
∵BP平分∠ABC,
∴PD=PC.
在Rt△BPD与Rt△BPC中,,
∴Rt△BPD≌Rt△BPC(HL),
∴BD=BC=6 cm,
∴AD=10﹣6=4 cm.
设PC=x cm,则PA=(8﹣x)cm
在Rt△APD中,PD2+AD2=PA2,
即x2+42=(8﹣x)2,
解得:x=3,
∴当t=3秒时,AP平分∠CAB;
(3)若P在边AC上时,BC=CP=6cm,
此时用的时间为6s,△BCP为等腰三角形;
若P在AB边上时,有两种情况:
①若使BP=CB=6cm,此时AP=4cm,P运动的路程为12cm,
所以用的时间为12s,故t=12s时△BCP为等腰三角形;
②若CP=BC=6cm,过C作斜边AB的高,根据面积法求得高为4.8cm,
根据勾股定理求得BP=7.2cm,
所以P运动的路程为18﹣7.2=10.8cm,
∴t的时间为10.8s,△BCP为等腰三角形;
③若BP=CP时,则∠PCB=∠PBC,
∵∠ACP+∠BCP=90°,∠PBC+∠CAP=90°,∴∠ACP=∠CAP,∴PA=PC
∴PA=PB=5cm
∴P的路程为13cm,所以时间为13s时,△BCP为等腰三角形.
∴t=6s或13s或12s或 10.8s 时△BCP为等腰三角形.
