2021-2022学年八年级数学人教版下册17.2勾股定理的逆定理课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年八年级数学人教版下册17.2勾股定理的逆定理课时练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 13:30:14 | ||
图片预览



文档简介
17.2《勾股定理的逆定理》课时练习
一、选择题
1.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
2.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
3.如图,在△ABC中,AD⊥BC于点D,BD=9,AD=12,AC=20,则△ABC是( )
A.等腰三角形 B.任意三角形
C.直角三角形 D.无法确定
4.如图所示的网格是正方形网格,则∠PAB+∠PBA( )度(点A,B,P是网格线交点)
A.30 B.45 C.60 D.90
5.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等边三角形
6.△ABC中,∠A>90°,AB=6,AC=8,则BC的长度可能是( )
A.8 B.10 C.12 D.14
7.如图,在4×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD⊥BC于点D,则AD的长为( )
A. B.2 C. D.3
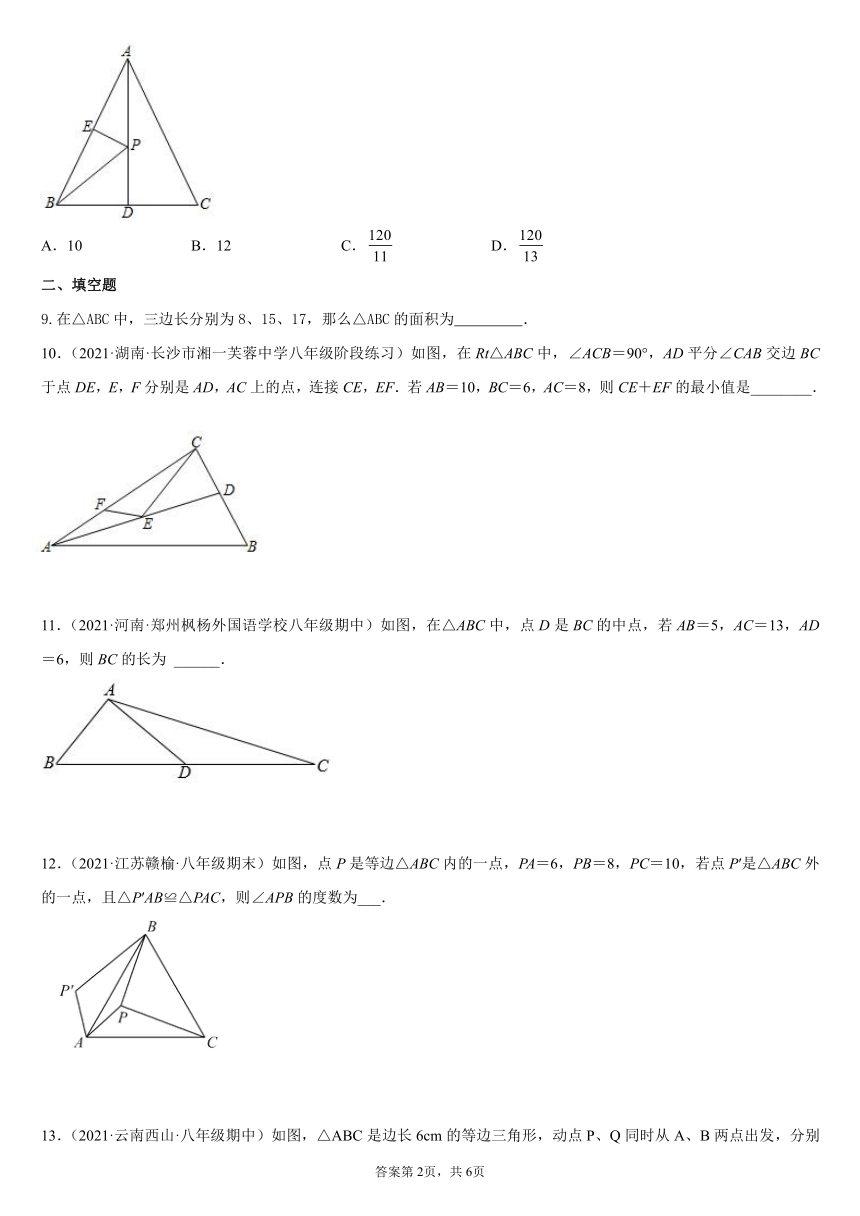
8.已知在等腰三角形ABC中,D为BC的中点AD=12,BD=5,AB=13,点P为AD边上的动点,点E为AB边上的动点,则PE+PB的最小值是( )
A.10 B.12 C. D.
二、填空题
9.在△ABC中,三边长分别为8、15、17,那么△ABC的面积为 .
10.(2021·湖南·长沙市湘一芙蓉中学八年级阶段练习)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
11.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
12.(2021·江苏赣榆·八年级期末)如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
13.(2021·云南西山·八年级期中)如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=___s时,△PBQ为直角三角形.
三、解答题
15.如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
16.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状
17.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求:
(1)△ABC的周长;
(2)△ABC是否是直角三角形?为什么?
18.已知a,b,c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4, 试判定△ABC的形状.
参考答案
1.B 2.C 3.C 4.B 5.C 6.C 7.B 8.D
9.答案为:60.
10【详解】
解:如图所示:在AB上取点,使,过点C作,垂足为H.
∵AB=10,BC=6,AC=8,
∴
∴是直角三角形,且
∴
∴,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为4.8,
故答案为:4.8.
11【详解】
解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
12.150°
解答.
【详解】
解:连接PP′,
∵△PAC≌△P′AB,
∴PA=P′A,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△APP′为等边三角形,
∴PP′=AP=AP′=6;
∵PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=90°+60°=150°.
故答案为:150°.
13.【详解】
∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6-2t,BQ=t,
∴6-2t=2t,
解得t= ;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴t=2(6-2t),
解得t= ,
∵0∴t=或t=
故答案为或.
14.答案为:3-2.
15.
解:∵AD=5dm,AC=10dm,CD=dm,
∴,
∴∠D=90°,
在直角△ADB中,BD=dm,
∴S△ABC=.
16.
解:是直角三角形,理由:
即,
∴是直角三角形.
解:(1)∵AD⊥BC,AD=12,BD=16
∴AB=
同理:AC=
∴△ABC的周长为AC+BC+AB=AC+BD+DC+AB=13+16+5+20=54;
(2)∵BC2=(BD+DC)2=212=441, AB2=202=400,AC2=132=169
∴BC2≠AB2+ AC2
∴△ABC不是直角三角形.
答案第1页,共2页
答案第8页,共1页
18.解:∵a2c2﹣b2c2=a4﹣b4 ,
∴a4﹣b4﹣a2c2+b2c2=0,
∴(a4﹣b4)﹣(a2c2﹣b2c2)=0,
∴(a2+b2)(a2﹣b2)﹣c2(a2﹣b2)=0,
∴(a2+b2﹣c2)(a2﹣b2)=0
得:a2+b2=c2或a=b,或者a2+b2=c2且a=b,
即△ABC为直角三角形或等腰三角形或等腰直角三角形.
一、选择题
1.下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.1,1, C.6,8,11 D.5,12,23
2.甲、乙两艘轮船同时从港口出发,甲以16海里/时的速度向北偏东的方向航行,它们出发1.5小时后,两船相距30海里,若乙以12海里/时的速度航行,则它的航行方向为( )
A.北偏西 B.南偏西75°
C.南偏东或北偏西 D.南偏西或北偏东
3.如图,在△ABC中,AD⊥BC于点D,BD=9,AD=12,AC=20,则△ABC是( )
A.等腰三角形 B.任意三角形
C.直角三角形 D.无法确定
4.如图所示的网格是正方形网格,则∠PAB+∠PBA( )度(点A,B,P是网格线交点)
A.30 B.45 C.60 D.90
5.三角形的三边长a,b,c满足2ab=(a+b)2-c2,则此三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等边三角形
6.△ABC中,∠A>90°,AB=6,AC=8,则BC的长度可能是( )
A.8 B.10 C.12 D.14
7.如图,在4×4的正方形网格中,每个小正方形的边长均为1,点A,B,C都在格点上,AD⊥BC于点D,则AD的长为( )
A. B.2 C. D.3
8.已知在等腰三角形ABC中,D为BC的中点AD=12,BD=5,AB=13,点P为AD边上的动点,点E为AB边上的动点,则PE+PB的最小值是( )
A.10 B.12 C. D.
二、填空题
9.在△ABC中,三边长分别为8、15、17,那么△ABC的面积为 .
10.(2021·湖南·长沙市湘一芙蓉中学八年级阶段练习)如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交边BC于点DE,E,F分别是AD,AC上的点,连接CE,EF.若AB=10,BC=6,AC=8,则CE+EF的最小值是________.
11.(2021·河南·郑州枫杨外国语学校八年级期中)如图,在△ABC中,点D是BC的中点,若AB=5,AC=13,AD=6,则BC的长为 ______.
12.(2021·江苏赣榆·八年级期末)如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为___.
13.(2021·云南西山·八年级期中)如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为Vp=2cm/s,VQ=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t=___s时,△PBQ为直角三角形.
三、解答题
15.如图,欲从一块三角形下脚料ADB中截出一个形如△ACD的工件,其中AD=5dm,AB=14dm,AC=10dm,CD=5dm,求剩余部分△ABC的面积.
16.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状
17.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求:
(1)△ABC的周长;
(2)△ABC是否是直角三角形?为什么?
18.已知a,b,c为△ABC的三边,且满足a2c2﹣b2c2=a4﹣b4, 试判定△ABC的形状.
参考答案
1.B 2.C 3.C 4.B 5.C 6.C 7.B 8.D
9.答案为:60.
10【详解】
解:如图所示:在AB上取点,使,过点C作,垂足为H.
∵AB=10,BC=6,AC=8,
∴
∴是直角三角形,且
∴
∴,
∵,
∴当C、E、共线,且点与H重合时,的值最小,最小值为4.8,
故答案为:4.8.
11【详解】
解:延长AD到E,使DE=AD,连接BE.
在△ADC与△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AC=BE=13.
在△ABE中,AB=5,AE=12,BE=13,
∴AB2+AE2=BE2,
∴∠BAE=90°.
在△ABD中,∠BAD=90°,AB=5,AD=6,
∴BD=,
∴BC=.
故答案为:.
12.150°
解答.
【详解】
解:连接PP′,
∵△PAC≌△P′AB,
∴PA=P′A,∠P′AB=∠PAC,
∴∠P′AP=∠BAC=60°,
∴△APP′为等边三角形,
∴PP′=AP=AP′=6;
∵PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=90°+60°=150°.
故答案为:150°.
13.【详解】
∵△ABC是等边三角形,
∴AB=BC=6cm,∠A=∠B=∠C=60°,
当∠PQB=90°时,∠BPQ=30°,
∴BP=2BQ.
∵BP=6-2t,BQ=t,
∴6-2t=2t,
解得t= ;
当∠QPB=90°时,∠PQB=30°,
∴BQ=2PB,
∴t=2(6-2t),
解得t= ,
∵0
故答案为或.
14.答案为:3-2.
15.
解:∵AD=5dm,AC=10dm,CD=dm,
∴,
∴∠D=90°,
在直角△ADB中,BD=dm,
∴S△ABC=.
16.
解:是直角三角形,理由:
即,
∴是直角三角形.
解:(1)∵AD⊥BC,AD=12,BD=16
∴AB=
同理:AC=
∴△ABC的周长为AC+BC+AB=AC+BD+DC+AB=13+16+5+20=54;
(2)∵BC2=(BD+DC)2=212=441, AB2=202=400,AC2=132=169
∴BC2≠AB2+ AC2
∴△ABC不是直角三角形.
答案第1页,共2页
答案第8页,共1页
18.解:∵a2c2﹣b2c2=a4﹣b4 ,
∴a4﹣b4﹣a2c2+b2c2=0,
∴(a4﹣b4)﹣(a2c2﹣b2c2)=0,
∴(a2+b2)(a2﹣b2)﹣c2(a2﹣b2)=0,
∴(a2+b2﹣c2)(a2﹣b2)=0
得:a2+b2=c2或a=b,或者a2+b2=c2且a=b,
即△ABC为直角三角形或等腰三角形或等腰直角三角形.
