2021-2022学年人教版数学八年级下册17.2勾股定理的逆定理同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册17.2勾股定理的逆定理同步习题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 471.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 13:30:34 | ||
图片预览


文档简介
第十七章17.2勾股定理的逆定理
一、选择题
1如图,有一个水池,水面是一边长为尺的正方形,在水池正中央有一根芦苇,它高出水面尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为尺.
A.
B.
C.
D.
2.适合下列条件的△ABC中, 直角三角形的个数为
①②,∠A=45°;③∠A=32°, ∠B=58°;
④⑤⑥
⑦⑹
A.2个 B.3个 C.4个 D.5个
3.(2019·山东德州·八年级期末)在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,下列说法中错误的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
4.(2020·广东·佛山市第十中学八年级阶段练习)如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A. B. C. D.
5如图,高速公路上有、两点相距,、为两村庄,已知,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是.
A. B. C. D.
6.如图,在四边形ABCD中,,,,,则四边形ABCD的面积是( ).
A.6 B.8 C.10 D.12
7.如图,在四边形中,,,,,,则四边形的面积为( )
A.122 B.114 C.110 D.100
8.如图,四边形中,,,,,,则四边形的面积为( )
A.100 B.110 C.114 D.122
二、填空题
9若两组勾股数从小到大依次是,,和,,,则的值是______.
10.三条线段分别长、、,且满足,以这三条线段为边组成的三角形为______.
11.观察下列勾股数:3,4,5;5,12,13;7,24,25;,,.根据你的发现,与之间的关系是_______,_______.
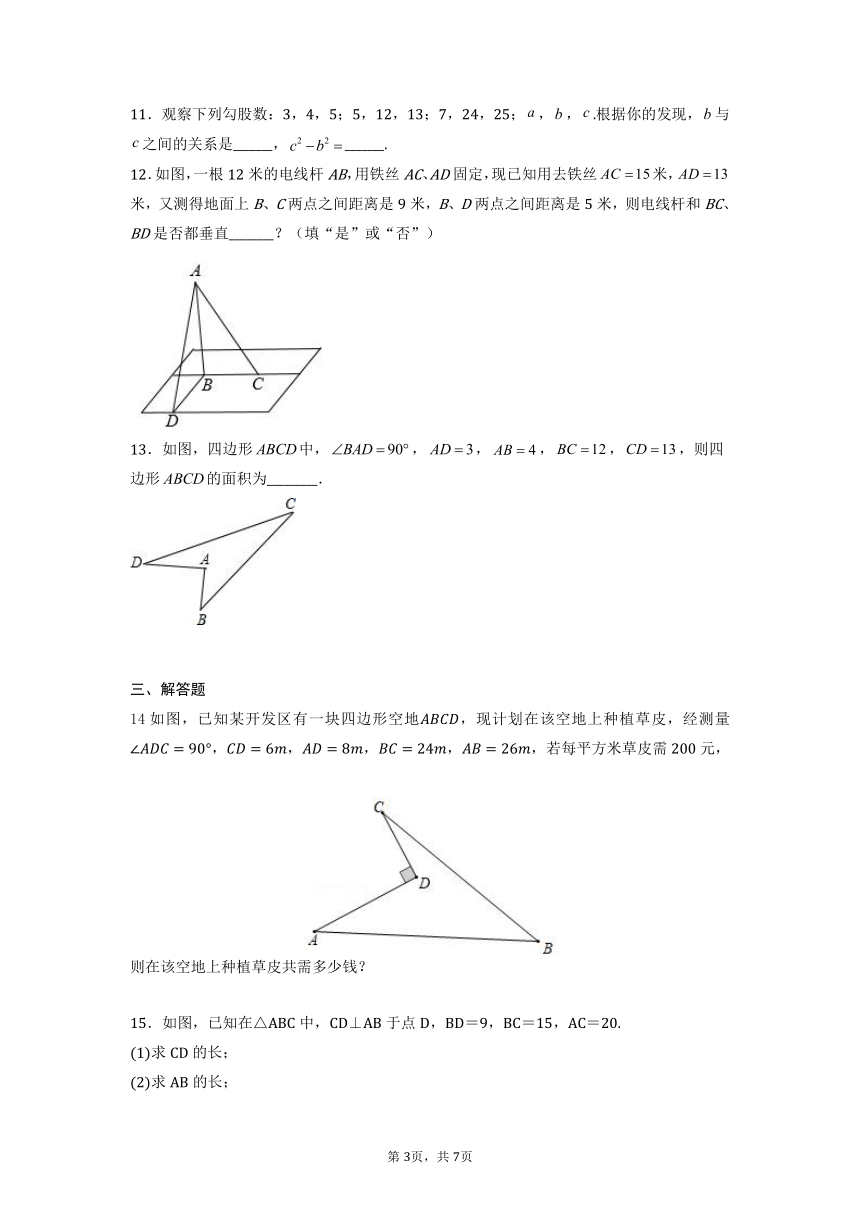
12.如图,一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝米,米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和BC、BD是否都垂直________?(填“是”或“否”)
13.如图,四边形中,,,,,,则四边形的面积为_________.
三、解答题
14如图,已知某开发区有一块四边形空地,现计划在该空地上种植草皮,经测量,,,,,若每平方米草皮需元,则在该空地上种植草皮共需多少钱?
15.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
16.如图,在正方形网格上有一个.
(1)发现与的数量关系是 ,位置关系是 .
(2)画关于直线的对称图形(不写画法);
(3)若网格上的每个小正方形的边长为1,则的面积为 .
(4)在直线MN上找一点P,使PA+PB最短.
17.如图,四边形ABCD中,∠A=90°,AB=AD=,CD=3,BC=.
(1)求∠ADC的度数.
(2)求四边形ABCD的面积.
18.(2021·陕西·西安交通大学附属中学航天学校八年级阶段练习)如图所示,在中,,点P从点A开始沿边向B点以每秒的速度移动,点Q从点B沿边向点C以每秒的速度移动,如果同时出发,问过3秒时,的面积为多少?
19.(2018·山东日照·中考真题)问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=AB.
探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
答案和解析
1.C 2.C 3.D 4.A 5.A 6.B 7.B 8.C
9【答案】
【解析】解:两组勾股数从小到大依次是,,和,,,
,,
,
故答案为:.
10.直角三角形
11.
12.是
13.24
14.【答案】解:连接,
在中,,
在中,,,
而,
即,
,
.
所以需费用元.
15.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
16.(1);;(2)略;(3)8.5;(4)略
17.(1)135°;(2)4
18.【详解】
解:AB=9,BC=12,AC=15,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,,BQ=2×3=6,
,
故过3秒时,△BPQ的面积为.
19【详解】探究结论(1),如图1中,
∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∵AC=AB=AE=EB,
∴△ACE是等边三角形,
∴EC=AE=EB,
故答案为:EC=EB;
(2)如图2中,结论:ED=EB.
理由:连接PE,
∵△ACP,△ADE都是等边三角形,
∴AC=AD=DE,AD=AE,∠CAP=∠DAE=60°,
∴∠CAD=∠PAE,
∴△CAD≌△PAE,
∴∠ACD=∠APE=90°,
∴EP⊥AB,∵PA=PB,
∴EA=EB,∵DE=AE,
∴ED=EB;
(3)当点D为边CB延长线上任意一点时,同法可证:ED=EB,
故答案为:ED=EB;
拓展应用:如图3中,作AH⊥x轴于H,CF⊥OB于F,连接OA,
∵A(﹣,1),
∴∠AOH=30°,
由(2)可知,CO=CB,
∵CF⊥OB,
∴OF=FB=1,
∴可以假设C(1,n),
∵OC=BC=AB,
∴1+n2=1+(+2)2,∴n=2+,∴C(1,2+).第6页,共7页
第7页,共7页
一、选择题
1如图,有一个水池,水面是一边长为尺的正方形,在水池正中央有一根芦苇,它高出水面尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度为尺.
A.
B.
C.
D.
2.适合下列条件的△ABC中, 直角三角形的个数为
①②,∠A=45°;③∠A=32°, ∠B=58°;
④⑤⑥
⑦⑹
A.2个 B.3个 C.4个 D.5个
3.(2019·山东德州·八年级期末)在△ABC中,∠A、∠B、∠C的对边分别为a,b,c,下列说法中错误的是( )
A.如果,那么 B.如果,那么
C.如果,那么 D.如果,那么
4.(2020·广东·佛山市第十中学八年级阶段练习)如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A. B. C. D.
5如图,高速公路上有、两点相距,、为两村庄,已知,于,于,现要在上建一个服务站,使得、两村庄到站的距离相等,则的长是.
A. B. C. D.
6.如图,在四边形ABCD中,,,,,则四边形ABCD的面积是( ).
A.6 B.8 C.10 D.12
7.如图,在四边形中,,,,,,则四边形的面积为( )
A.122 B.114 C.110 D.100
8.如图,四边形中,,,,,,则四边形的面积为( )
A.100 B.110 C.114 D.122
二、填空题
9若两组勾股数从小到大依次是,,和,,,则的值是______.
10.三条线段分别长、、,且满足,以这三条线段为边组成的三角形为______.
11.观察下列勾股数:3,4,5;5,12,13;7,24,25;,,.根据你的发现,与之间的关系是_______,_______.
12.如图,一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝米,米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电线杆和BC、BD是否都垂直________?(填“是”或“否”)
13.如图,四边形中,,,,,,则四边形的面积为_________.
三、解答题
14如图,已知某开发区有一块四边形空地,现计划在该空地上种植草皮,经测量,,,,,若每平方米草皮需元,则在该空地上种植草皮共需多少钱?
15.如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.
16.如图,在正方形网格上有一个.
(1)发现与的数量关系是 ,位置关系是 .
(2)画关于直线的对称图形(不写画法);
(3)若网格上的每个小正方形的边长为1,则的面积为 .
(4)在直线MN上找一点P,使PA+PB最短.
17.如图,四边形ABCD中,∠A=90°,AB=AD=,CD=3,BC=.
(1)求∠ADC的度数.
(2)求四边形ABCD的面积.
18.(2021·陕西·西安交通大学附属中学航天学校八年级阶段练习)如图所示,在中,,点P从点A开始沿边向B点以每秒的速度移动,点Q从点B沿边向点C以每秒的速度移动,如果同时出发,问过3秒时,的面积为多少?
19.(2018·山东日照·中考真题)问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt△ABC中,∠ACB=90°,∠ABC=30°,则:AC=AB.
探究结论:小明同学对以上结论作了进一步研究.
(1)如图1,连接AB边上中线CE,由于CE=AB,易得结论:①△ACE为等边三角形;②BE与CE之间的数量关系为 .
(2)如图2,点D是边CB上任意一点,连接AD,作等边△ADE,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.
(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论 .
拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.
答案和解析
1.C 2.C 3.D 4.A 5.A 6.B 7.B 8.C
9【答案】
【解析】解:两组勾股数从小到大依次是,,和,,,
,,
,
故答案为:.
10.直角三角形
11.
12.是
13.24
14.【答案】解:连接,
在中,,
在中,,,
而,
即,
,
.
所以需费用元.
15.(1)CD长为12;(2)AB的长为25;(3)△ABC是直角三角形
16.(1);;(2)略;(3)8.5;(4)略
17.(1)135°;(2)4
18.【详解】
解:AB=9,BC=12,AC=15,
∵AB2+BC2=AC2,
∴△ABC是直角三角形,
过3秒时,,BQ=2×3=6,
,
故过3秒时,△BPQ的面积为.
19【详解】探究结论(1),如图1中,
∵∠ACB=90°,∠B=30°,
∴∠A=60°,
∵AC=AB=AE=EB,
∴△ACE是等边三角形,
∴EC=AE=EB,
故答案为:EC=EB;
(2)如图2中,结论:ED=EB.
理由:连接PE,
∵△ACP,△ADE都是等边三角形,
∴AC=AD=DE,AD=AE,∠CAP=∠DAE=60°,
∴∠CAD=∠PAE,
∴△CAD≌△PAE,
∴∠ACD=∠APE=90°,
∴EP⊥AB,∵PA=PB,
∴EA=EB,∵DE=AE,
∴ED=EB;
(3)当点D为边CB延长线上任意一点时,同法可证:ED=EB,
故答案为:ED=EB;
拓展应用:如图3中,作AH⊥x轴于H,CF⊥OB于F,连接OA,
∵A(﹣,1),
∴∠AOH=30°,
由(2)可知,CO=CB,
∵CF⊥OB,
∴OF=FB=1,
∴可以假设C(1,n),
∵OC=BC=AB,
∴1+n2=1+(+2)2,∴n=2+,∴C(1,2+).第6页,共7页
第7页,共7页
