2022年苏科版七年级数学下册7.3 图形的平移 课时练习(Word版含答案)
文档属性
| 名称 | 2022年苏科版七年级数学下册7.3 图形的平移 课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 177.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 15:51:58 | ||
图片预览




文档简介
7.3《图形的平移》课时练习
一、选择题
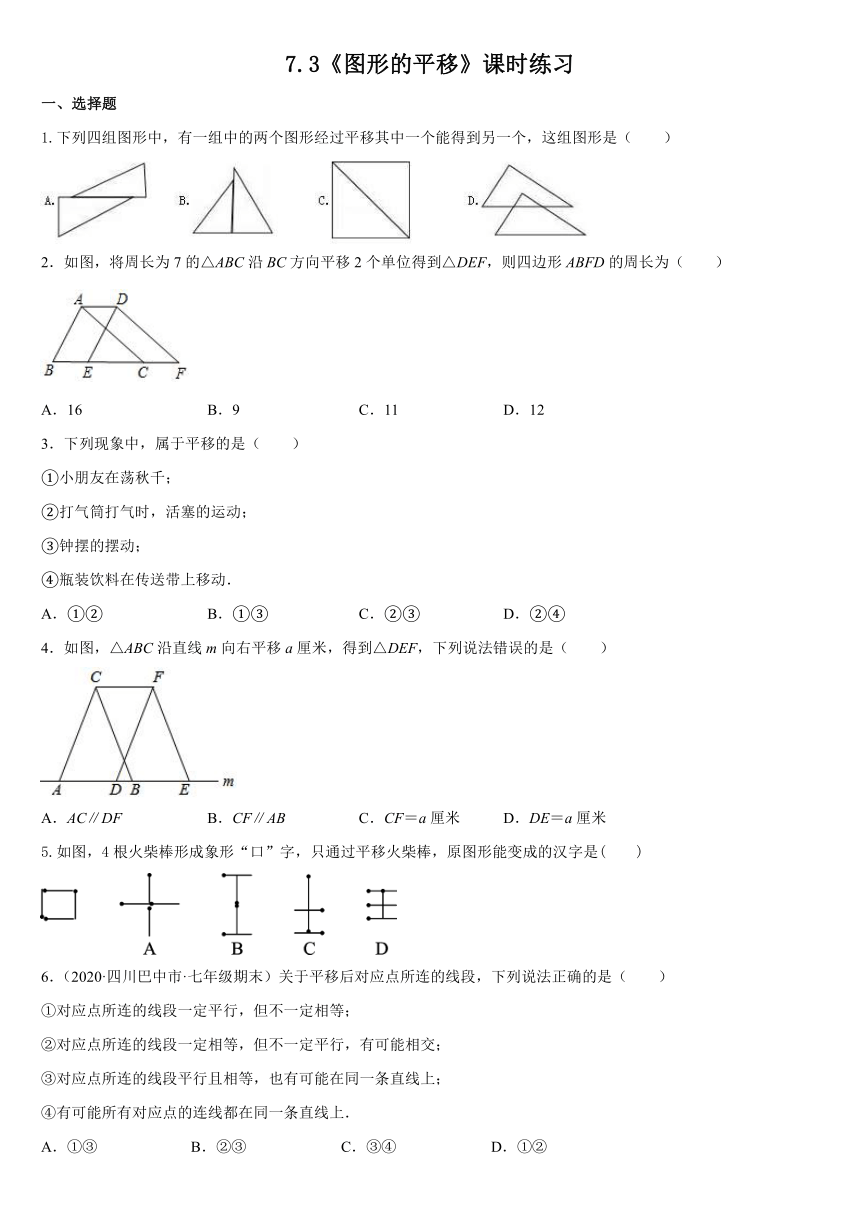
1.下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
2.如图,将周长为7的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.16 B.9 C.11 D.12
3.下列现象中,属于平移的是( )
①小朋友在荡秋千;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
4.如图,△ABC沿直线m向右平移a厘米,得到△DEF,下列说法错误的是( )
A.AC∥DF B.CF∥AB C.CF=a厘米 D.DE=a厘米
5.如图,4根火柴棒形成象形“口”字,只通过平移火柴棒,原图形能变成的汉字是( )
6.(2020·四川巴中市·七年级期末)关于平移后对应点所连的线段,下列说法正确的是( )
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③ B.②③ C.③④ D.①②
7.(2020·东营市实验中学七年级月考)如图,两个直角三角形重叠在一起,将沿AB方向平移得到,,,下列结论:①;②;③:④;⑤阴影部分的面积为.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
8.(2020·河南七年级期末)把△ABC沿方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
A.增大 B.减小 C.不变 D.不确定
二、填空题
9.如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是 .
10.如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.
11.已知线段AB的长度为3厘米,现将线段AB向左平移4厘米得到线段CD,那么线段CD的长度为 厘米.
12.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为 .
13.如图是用三角尺和直尺画平行线的示意图,将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置,就可以画出AB的平行线A′B′.若AC′=9cm,A′C=2cm,则直线AB平移的距离为 cm.
14.如图,台阶的宽度为1.5米,其高度AB=4米,水平距离BC=5米,要在台阶上铺满地毯,则地毯的面积为 .
三、解答题
15、如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
16、如图,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
17、如图,在边长为1的小正方形方格纸中,△ABC的项点都在方格纸格点上,将△ABC向左平移1格,再向上平移4格
(1)请在图中画出平移后的△A1B1C1;
(2)连接AA1、 BB1、CC1,则它们的关系是
18、如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是
(4)△ABC在整个平移过程中线段AB扫过的面积为
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个
(注:格点指网格线的交点)
参考答案
1.D 2.C 3.D 4.D 5.B 6.C 7.A 8.C
9.答案为:4;
10.答案为:A(B或C),A’(B’或C’) ,AA’(BB’或CC’)
11.答案为:3.
12.答案为:3.
13.案为:5.5.
14.答案为:13.5平方米.
15、答案(1)平移的方向是点A到点D的方向,平移的距离是线段的长度;(2)见解析
16、如图,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
解:如图:四边形A′B′C′D′即为所求.
17【答案】(1)见解析;(2)平行且相等
【分析】
(1)将点、点、点,分别向左平移1格,再向上平移4格,得到、、,连接即可.
(2)根据平移的性质,即可得到答案.
【详解】
(1)见下图;
(2)如下图:
根据平移的性质知:、、的关系是平行且相等.
18、如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是
(4)△ABC在整个平移过程中线段AB扫过的面积为
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个
(注:格点指网格线的交点)
【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可;
(2)利用网格特点找出A′C′的中点D′,然后连接B′D′即可;
(3)根据平移的性质求解;
(4)利用平移的性质和平行四边形的面积公式求解;
(5)过点C作AB的平行线,然后找出此平行线上的格点即可.
【解答】解:(1)如图,△A′B′C′为所作;
(2)如图,中线B′D′为所作;
(3)BB′∥CC′,BB′=CC′;
(4)△ABC在整个平移过程中线段AB扫过的面积=4×3=12;
(5)满足条件且异于点C的格点E共有10个.
故答案为BB′∥CC′,BB′=CC′;12;10.
一、选择题
1.下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是( )
2.如图,将周长为7的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为( )
A.16 B.9 C.11 D.12
3.下列现象中,属于平移的是( )
①小朋友在荡秋千;
②打气筒打气时,活塞的运动;
③钟摆的摆动;
④瓶装饮料在传送带上移动.
A.①② B.①③ C.②③ D.②④
4.如图,△ABC沿直线m向右平移a厘米,得到△DEF,下列说法错误的是( )
A.AC∥DF B.CF∥AB C.CF=a厘米 D.DE=a厘米
5.如图,4根火柴棒形成象形“口”字,只通过平移火柴棒,原图形能变成的汉字是( )
6.(2020·四川巴中市·七年级期末)关于平移后对应点所连的线段,下列说法正确的是( )
①对应点所连的线段一定平行,但不一定相等;
②对应点所连的线段一定相等,但不一定平行,有可能相交;
③对应点所连的线段平行且相等,也有可能在同一条直线上;
④有可能所有对应点的连线都在同一条直线上.
A.①③ B.②③ C.③④ D.①②
7.(2020·东营市实验中学七年级月考)如图,两个直角三角形重叠在一起,将沿AB方向平移得到,,,下列结论:①;②;③:④;⑤阴影部分的面积为.其中正确的是( )
A.①②③④⑤ B.②③④⑤ C.①②③⑤ D.①②④⑤
8.(2020·河南七年级期末)把△ABC沿方向平移,得到△A′B′C′,随着平移距离的不断增大,△A′CB的面积大小变化情况是( )
A.增大 B.减小 C.不变 D.不确定
二、填空题
9.如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是 .
10.如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.
11.已知线段AB的长度为3厘米,现将线段AB向左平移4厘米得到线段CD,那么线段CD的长度为 厘米.
12.如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为 .
13.如图是用三角尺和直尺画平行线的示意图,将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置,就可以画出AB的平行线A′B′.若AC′=9cm,A′C=2cm,则直线AB平移的距离为 cm.
14.如图,台阶的宽度为1.5米,其高度AB=4米,水平距离BC=5米,要在台阶上铺满地毯,则地毯的面积为 .
三、解答题
15、如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
16、如图,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
17、如图,在边长为1的小正方形方格纸中,△ABC的项点都在方格纸格点上,将△ABC向左平移1格,再向上平移4格
(1)请在图中画出平移后的△A1B1C1;
(2)连接AA1、 BB1、CC1,则它们的关系是
18、如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是
(4)△ABC在整个平移过程中线段AB扫过的面积为
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个
(注:格点指网格线的交点)
参考答案
1.D 2.C 3.D 4.D 5.B 6.C 7.A 8.C
9.答案为:4;
10.答案为:A(B或C),A’(B’或C’) ,AA’(BB’或CC’)
11.答案为:3.
12.答案为:3.
13.案为:5.5.
14.答案为:13.5平方米.
15、答案(1)平移的方向是点A到点D的方向,平移的距离是线段的长度;(2)见解析
16、如图,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
解:如图:四边形A′B′C′D′即为所求.
17【答案】(1)见解析;(2)平行且相等
【分析】
(1)将点、点、点,分别向左平移1格,再向上平移4格,得到、、,连接即可.
(2)根据平移的性质,即可得到答案.
【详解】
(1)见下图;
(2)如下图:
根据平移的性质知:、、的关系是平行且相等.
18、如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是
(4)△ABC在整个平移过程中线段AB扫过的面积为
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有 个
(注:格点指网格线的交点)
【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可;
(2)利用网格特点找出A′C′的中点D′,然后连接B′D′即可;
(3)根据平移的性质求解;
(4)利用平移的性质和平行四边形的面积公式求解;
(5)过点C作AB的平行线,然后找出此平行线上的格点即可.
【解答】解:(1)如图,△A′B′C′为所作;
(2)如图,中线B′D′为所作;
(3)BB′∥CC′,BB′=CC′;
(4)△ABC在整个平移过程中线段AB扫过的面积=4×3=12;
(5)满足条件且异于点C的格点E共有10个.
故答案为BB′∥CC′,BB′=CC′;12;10.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
