2022年人教版八年级数学下册17.2 勾股定理的逆定理 随堂练习(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册17.2 勾股定理的逆定理 随堂练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 160.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 16:00:53 | ||
图片预览


文档简介
17.2《勾股定理的逆定理》随堂练习
一、单选题
1.下列各组数中不能作为直角三角形的三边长的是( ).
A.1.5,2,2 B.7,24,25 C.6,8,10 D.9,12,15
2.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个 B.5个 C.6个 D.8个
3.三角形三边长分别是6,10,8,则它的最长边上的高为( )
A.6 B.10 C.8 D.4.8
4.若的三边a、b、c满足,则的面积是( )
A. B. C. D.
5.一个三角形三边长a,b,c满足|a-12|++(c-20)2=0,则这个三角形最长边上的高为( )
A.9.8 B.4.8 C.9.6 D.10
6.(2010·四川眉山·中考真题)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
7.(2021·河北临西·八年级阶段练习)已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
8.(2020·山东滨城·八年级期末)在中,是直线上一点,已知,,,,则的长为( )
A.4或14 B.10或14 C.14 D.10
二、填空题
9.若三角形三边长分别为15,12,9,则这个三角形最长边上的高是____.
10.有四个三角形,分别满足下列条件:
(1)一个内角等于另外两个内角之和;
(2)三个内角之比为3:4:5;
(3)三边之比为5:12:13;
(4)三边长分别为7、24、25.
其中直角三角形有 个.
11.小明同学要做一个直角三角形小铁架,他现有4根长度分别为4cm、6cm、8cm、10cm的铁棒,可用于制作成直角三角形铁架的三条铁棒分别是____________;
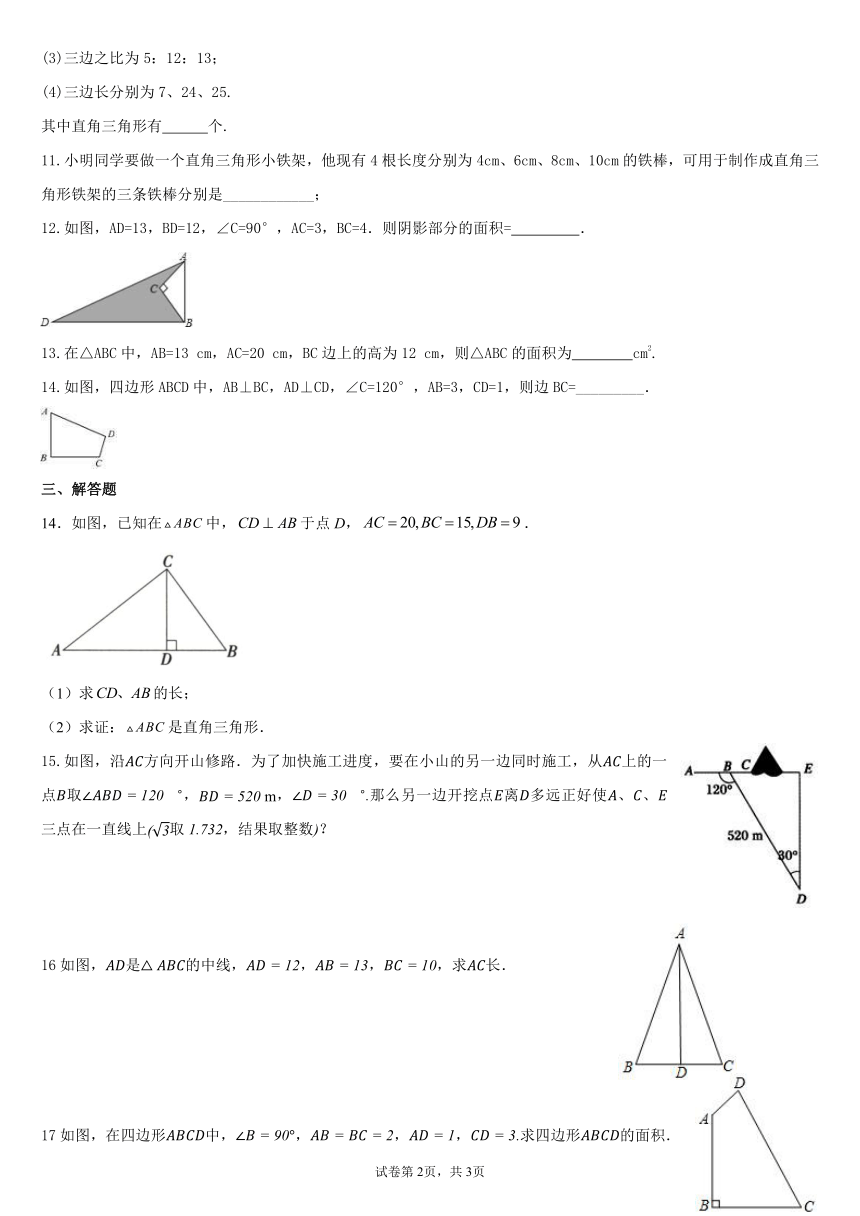
12.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= .
13.在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积为 cm2.
14.如图,四边形ABCD中,AB⊥BC,AD⊥CD,∠C=120°,AB=3,CD=1,则边BC=_________.
三、解答题
14.如图,已知在中,于点D,.
(1)求的长;
(2)求证:是直角三角形.
15.如图,沿方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从上的一点取,,那么另一边开挖点离多远正好使、、三点在一直线上取,结果取整数?
16如图,是的中线,,,,求长.
17如图,在四边形中,,,,求四边形的面积.
18.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.A 2.C 3.D 4.B 5.C 6.C 7.C 8.A
9.
10.答案为:3.
11.答案为:6cm、8cm、10cm
12.答案为:24.
13.答案为:66或126.
14.
解:(1)∵于点D,
∴和是直角三角形,
在中,,
∴.
在中,,
∴.
∴;
(2)证明:∵,
∴,
,
∴是直角三角形.
15.【答案】解:,,
,
在中,,,
,
.
答:另一边开挖点离,正好使,,三点在一直线上.
【解析】本题考查三角形的外角性质与勾股定理的应用.关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,领会数形结合的思想的应用.
根据三角形内角与外角的关系可求出的度数,再根据勾股定理即可求出的长.
16.【答案】解:是的中线,且,
.
,即,
是直角三角形,则,
又,
.
17.【答案】解:连接,
,,
,,
,,
,,
,
是直角三角形,
,
在中,,
在中,,
.
【解析】本题考查了勾股定理及勾股定理的逆定理的运用,考查了直角三角形面积计算,属于基础题.
连接,则可以计算的面积,根据勾股定理的逆定理可以判定为直角三角形,即可得解.
18(1)锐角;(2)169或119;(3)略
答案第4页,共2页
答案第5页,共2页
一、单选题
1.下列各组数中不能作为直角三角形的三边长的是( ).
A.1.5,2,2 B.7,24,25 C.6,8,10 D.9,12,15
2.在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为5,且△ABC是直角三角形,则满足条件的C点有( )
A.4个 B.5个 C.6个 D.8个
3.三角形三边长分别是6,10,8,则它的最长边上的高为( )
A.6 B.10 C.8 D.4.8
4.若的三边a、b、c满足,则的面积是( )
A. B. C. D.
5.一个三角形三边长a,b,c满足|a-12|++(c-20)2=0,则这个三角形最长边上的高为( )
A.9.8 B.4.8 C.9.6 D.10
6.(2010·四川眉山·中考真题)如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
7.(2021·河北临西·八年级阶段练习)已知,为正数,且,如果以,的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )
A.5 B.25 C.7 D.15
8.(2020·山东滨城·八年级期末)在中,是直线上一点,已知,,,,则的长为( )
A.4或14 B.10或14 C.14 D.10
二、填空题
9.若三角形三边长分别为15,12,9,则这个三角形最长边上的高是____.
10.有四个三角形,分别满足下列条件:
(1)一个内角等于另外两个内角之和;
(2)三个内角之比为3:4:5;
(3)三边之比为5:12:13;
(4)三边长分别为7、24、25.
其中直角三角形有 个.
11.小明同学要做一个直角三角形小铁架,他现有4根长度分别为4cm、6cm、8cm、10cm的铁棒,可用于制作成直角三角形铁架的三条铁棒分别是____________;
12.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= .
13.在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积为 cm2.
14.如图,四边形ABCD中,AB⊥BC,AD⊥CD,∠C=120°,AB=3,CD=1,则边BC=_________.
三、解答题
14.如图,已知在中,于点D,.
(1)求的长;
(2)求证:是直角三角形.
15.如图,沿方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从上的一点取,,那么另一边开挖点离多远正好使、、三点在一直线上取,结果取整数?
16如图,是的中线,,,,求长.
17如图,在四边形中,,,,求四边形的面积.
18.阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
试卷第2页,共3页
试卷第3页,共3页
参考答案
1.A 2.C 3.D 4.B 5.C 6.C 7.C 8.A
9.
10.答案为:3.
11.答案为:6cm、8cm、10cm
12.答案为:24.
13.答案为:66或126.
14.
解:(1)∵于点D,
∴和是直角三角形,
在中,,
∴.
在中,,
∴.
∴;
(2)证明:∵,
∴,
,
∴是直角三角形.
15.【答案】解:,,
,
在中,,,
,
.
答:另一边开挖点离,正好使,,三点在一直线上.
【解析】本题考查三角形的外角性质与勾股定理的应用.关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图,领会数形结合的思想的应用.
根据三角形内角与外角的关系可求出的度数,再根据勾股定理即可求出的长.
16.【答案】解:是的中线,且,
.
,即,
是直角三角形,则,
又,
.
17.【答案】解:连接,
,,
,,
,,
,,
,
是直角三角形,
,
在中,,
在中,,
.
【解析】本题考查了勾股定理及勾股定理的逆定理的运用,考查了直角三角形面积计算,属于基础题.
连接,则可以计算的面积,根据勾股定理的逆定理可以判定为直角三角形,即可得解.
18(1)锐角;(2)169或119;(3)略
答案第4页,共2页
答案第5页,共2页
