反比例函数复习

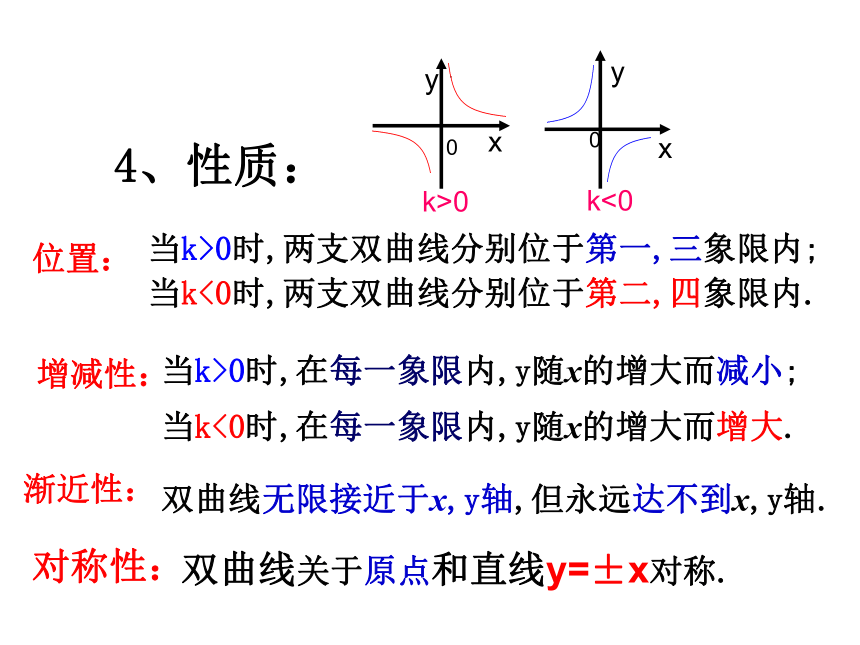
课件34张PPT。反比例函数复习课尚义二中 八年级数学备课组知识回顾1、反比例函数解析式 2、自变量取值范围是x≠0的一切实数3、图象：双曲线4、性质：当k>0时,两支双曲线分别位于第一,三象限内;
当k<0时,两支双曲线分别位于第二,四象限内.双曲线关于原点和直线y=±x对称.双曲线无限接近于x,y轴,但永远达不到x,y轴.当k>0时,在每一象限内,y随x的增大而减小;
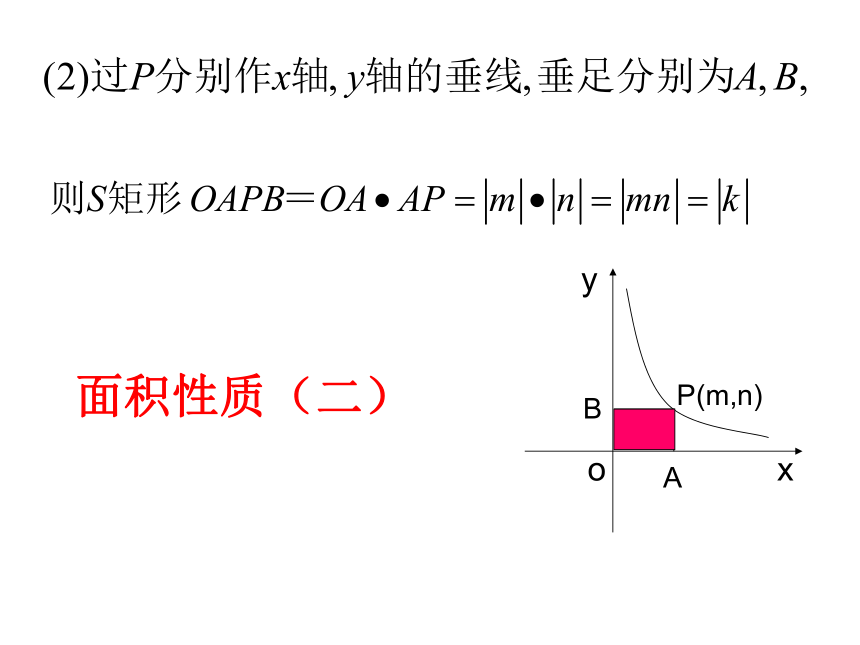
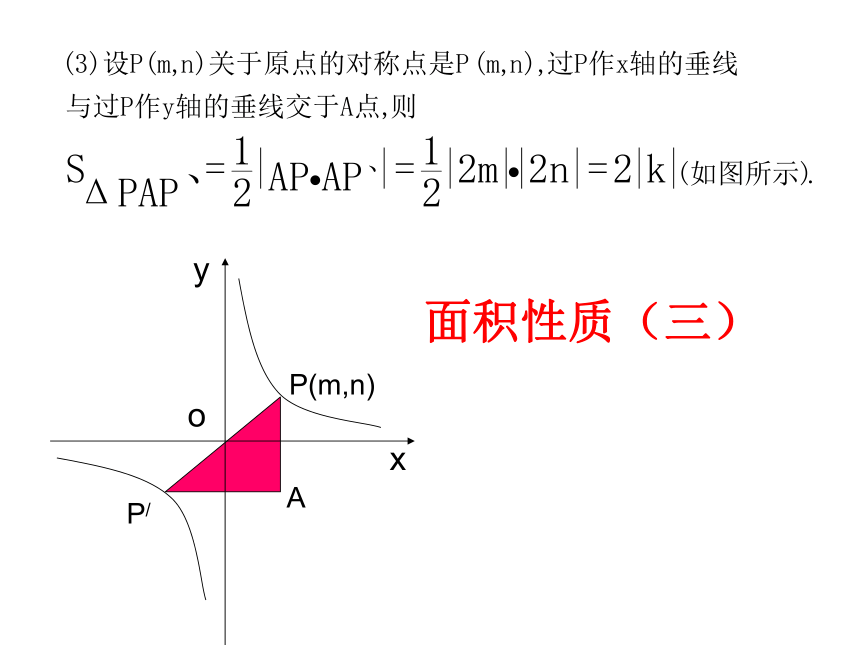
当k<0时,在每一象限内,y随x的增大而增大.位置：增减性：渐近性：对称性：5、与面积有关的问题：面积性质（一）：面积性质（二）面积性质（三）数学思想方法1、分类讨论思想；4、待定系数法。3、数学建模思想；2、数形结合思想；考点一反比例函数的概念问题考点例析1、在下列函数中，是反比例函数的有 .2、已知反比例函数 ,
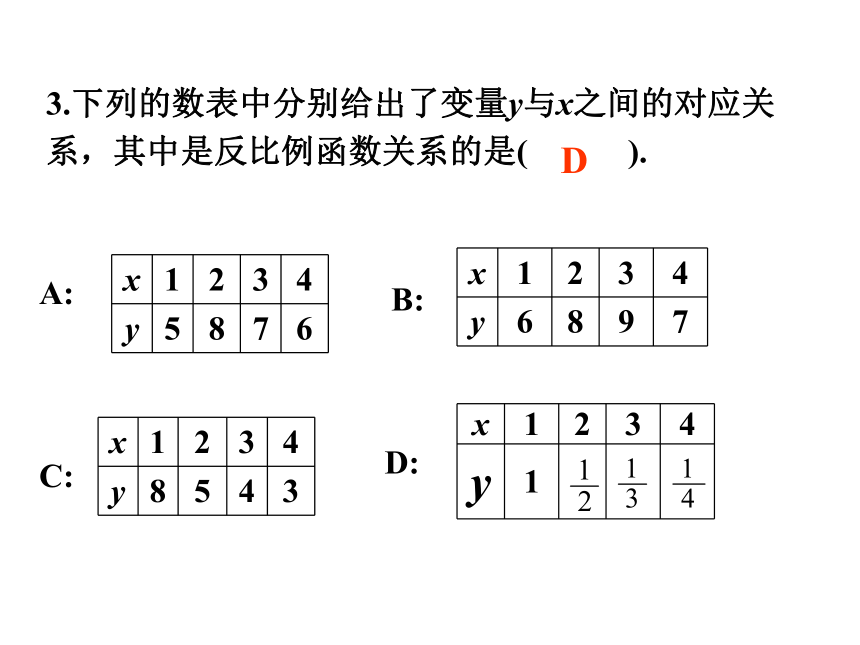
求a的值和表达式.3.下列的数表中分别给出了变量y与x之间的对应关系，其中是反比例函数关系的是( ).
A:C:D:B:D考点二 求反比例函数
的解析式1、已知y 与 x 成反比例, 并且当 x = 5 时 y = －3，
（1）求 y与 x 的函数关系式；
（2）当x=－15时，求y的值；
（3）当y=6时，求x的值。3、如图反比例函数 与直线y=－2x相交于点A，点A的横坐标为－1，则此反比例函数的解析式为（ ）C考点三反比例函数的
图象与性质1、写出一个图象分布在第二、四象限内的反比例函数解析式是 .2、已知反比例函数 的图象在第一、三象限，则a的取值范围是（ ）
（A）a≤2 （B） a≥2 （C） a＜2 （D） a＞2 3、已知反比例函数的图象经过点A（-5，6）
（1）这个函数的图象分布在哪些象限？
y随x的增大如何变化？
（2）点B（-30，1）、C（-2 ，15）和
D（-2，-15）是否在这个函数的图象上？ D4、如图是反比例函数 的图象的一支，根据图象回答下列问题： (2)已知点（－3，y1）,
（－1，y2）, （2，y3）,
则函数值y1、y2、y3的
大小关系怎样？(1)图象的另一支在哪个象限?
常数m的取值范围是什么?D7.考察函数 的图象,
(1)当x=-2时,y= ,
(2)当x<-2时,y的取值范围是 ;
(3)当y≥-1时,x的取值范围是 .-1y>-1x>0或x<-2考点四反比例函数与一次函数的综合题1、一次函数y=2x-5的图象与反比例函数 的图象交于第四象限的一点P（a，-3a），则这个反比例函数的解析式为 .2、正比例函数y=x与反比例函数y= 的图象相交于
A、C两点.AB⊥x轴于B,CD⊥y轴于D(如图),则四边形ABCD的面积为( )
（A）1 （B）
（C）2 （D）C3、如图，直线y=-2x-2与双曲线 交于点A，与x轴、y轴分别交于点B、C，AD⊥x轴于点D，如果S△ADB=S△CDB，那么k= .4、正比例函数y=x的图象与反比例函数y= 的图象有一个交点的纵坐标是2，
求（1）x=-3时反比例函数y的值；
（2）当-3 交于M(2，m)、N(-1，-4)两点.
（1）求反比例函数和一
次函数的解析式；
（2）根据图象写出反比
例函数的值大于一
次函数的值的x的取
值范围.7、 直线y=kx与反比例函数y=－ 的图象相交
于点A、B，过点A作AC垂直于y轴于点C，求S△ABC．8．如图所示，已知直线y1=x+m与x轴、y轴分别交于点A、B，与双曲线y2= （k<0）分别交于点C、D，且C点坐标为（-1，2）． (3）利用图象直接写出当x在什么范围内取何值时，y1>y2．（2）求出点D的坐标；（1）分别求直线AB与双曲线的解析式；（4）试着在坐标轴上找
点D,使△AOD≌△BOC。（1）分别写出这两个函数的表达式。（2）你能求出点B的坐标吗？
你是怎样求的？（3）若点C坐标是（–4，0）.
请求△BOC的面积。（4，0）考点五实际问题与反比例函数1.某蓄电池的电压为定值。右图表示的是该蓄电池
电流I 与电阻R之间的函数关系。如图，则函数的
解析式为____________.
（A）I=36/R （B）I =18/R
（C）I=9/R （D）I=72/R2.某气球内充满了一定质量的气体，当温度不变时，气球
内气体的气压P与气体体积V的关系为P=96/V，规定气球
的气压不得超过120，符合规定时，气球内气体的体积应
为___________.
（A）不超过0.8 （B）不低于0.8
（C）不超过1.25 （D）不低于1.25AB3.某商场出售一种进价为2元的贺卡,在市场营销中发现此商品的日销售价x与日销售量y个之间的关系如下表:
(1)根据表中数据,在直角坐标系
中描出实数对(x,y)的对应点;
(2)猜测并确定 y与x之间的函数关系式,并画出图象;
(3)设经营此卡的销售利润为w元,试求出w
与x之间的函数关系,若物价局规定此贺卡
的销售价最高不超过10元,请求出当日销售
价x定为多少元时,才能使所获利润最大?4.某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD。该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米. 设健身房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元。
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12。当投入资金为4800元时，问利用旧墙壁的总长度为多少米？5.制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？ 6.如图，正方形OABC的面积为9，点O为坐标原点，点B在函数y= (k>0,x>0)的图象上，点P（m, n）是函数y= (k>0,x>0)的图象上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF和正方形OABC不重合部分的面积为S。（提示：考虑点P在点B的左侧或右侧两种情况）
（1）求B点坐标和k的值；
（2）当S= 时，求点P的坐标；
（3）写出S与m的函数关系式。1、将 代入反比例函数 中，所得的函数值记为y1，将x2=y1+1代入反比例 函数中，所得的函数值记为y2，将x3+1代入反比例函数 中，所得的函数值y3记为，…，将xn代入反比例函数中，所得的函数值记为yn，(其中n≥2，且n是自然数)，如此继续下去。则在2005个函数值y1，y2，y3，……，yn中，值为2的情况共出现了 次。 规律探究型问题2、（2005年中考·湖州）两个反比例函数 ，在第一象限内的图象如图所示，点P1，P2，P3，…，
P2005在反比例函数y= 图象上，它们的横坐标分别是
x1，x2，x3，…，x2005，纵坐标分别1，3，5，…，共2005年连续奇数，过点P1，P2，P3，…，P2005分别作y轴
的平行线，与y= 的图象
交点依次是Q1（x1，y1），
Q2（x2，y2），Q3（x3，y3），
…，Q2005（x2005，y2005），
则y2005= ．2004.5