2021-2022学年人教版八年级下 19.3课题学习 选择方案同步练习(含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级下 19.3课题学习 选择方案同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 18:29:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级下 19.3课题学习 选择方案同步练习
一.选择题
1.(2021秋 南岸区期末)某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.则y与x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
2.(2021春 永春县期末)已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
3.(2021秋 大东区期末)弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
4.(2020 西藏)如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
5.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的函数图象如图所示,函数关系式为y=kx﹣600,则旅客携带50kg行李时的运费为( )
A.300元 B.500元 C.600元 D.900元
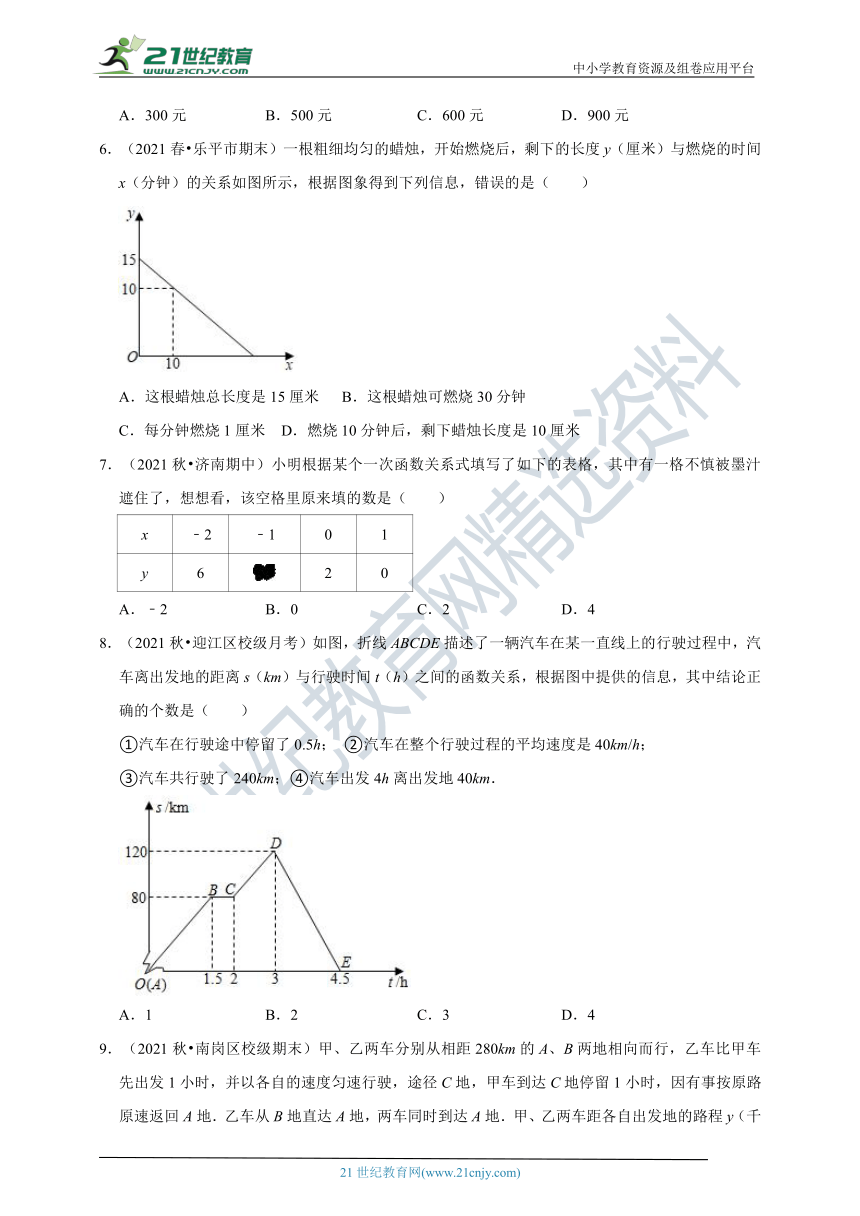
6.(2021春 乐平市期末)一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米 B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米 D.燃烧10分钟后,剩下蜡烛长度是10厘米
7.(2021秋 济南期中)小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
x ﹣2 ﹣1 0 1
y 6 2 0
A.﹣2 B.0 C.2 D.4
8.(2021秋 迎江区校级月考)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,其中结论正确的个数是( )
①汽车在行驶途中停留了0.5h; ②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;④汽车出发4h离出发地40km.
A.1 B.2 C.3 D.4
9.(2021秋 南岗区校级期末)甲、乙两车分别从相距280km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法:
①乙车的速度是40千米/时; ②甲车从C返回A的速度为70千米/时;
③t=3; ④当两车相距35千米时,乙车行驶的时间是2小时或6小时;
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.(2021春 梁平区期末)张伟骑摩托车从甲地去乙地,李亮开汽车从乙地去甲地,两人同时出发,匀速行驶,各自到达终点后停止,设张伟、李亮两人间的距离为s(单位:千米),张伟行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发3小时时,张伟和李亮同时到达终点;②张伟骑摩托车的速度为千米/小时;
③李亮开汽车的速度为60千米/小时;④出发1.5小时时,李亮比张伟多行驶50千米;
上述结论正确的是( )
A.①② B.③④ C.②④ D.②③④
二.填空题
11.(2020秋 烈山区期中)等腰三角形的周长为16cm,底边长为ycm,腰长为xcm,则y与x之间的关系式为 ,自变量x的取值范围为 .
12.(2020春 高州市期中)空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 m.
13.(2021秋 拱墅区月考)一水池蓄水20m3,打开阀门后每小时流出5m3,放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为 ,自变量t的取值范围 .
14.(2021春 丰台区校级期中)在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 .(填序号)
15.(2020秋 开江县期末)关于函数y=kx+3+k(k为常数),给出下列结论:①此函数是一次函数;②无论k取什么值,函数图象必经过点(﹣1,3);③若k>0时,函数图象经过第一、二、三象限;④若k<0时,函数图象与x轴的交点始终在负半轴上.其中正确的是 (填序号).
16.(2021秋 锦州期末)平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 .
17.(2020秋 浦东新区校级期末)正比例函数y=kx的图象上一点P到x轴的距离为2,点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,则k的值为 .
三.解答题
18.(2021秋 任城区期末)我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.
(1)请直接写出y与x之间的函数关系式;
(2)此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃.求飞机离地的高度是多少千米?
19.(2021秋 禅城区期末)学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元;购买甲奖品3个和乙奖品2个,需花费44元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;
(3)在(2)的条件下,问买哪一种产品更省钱?
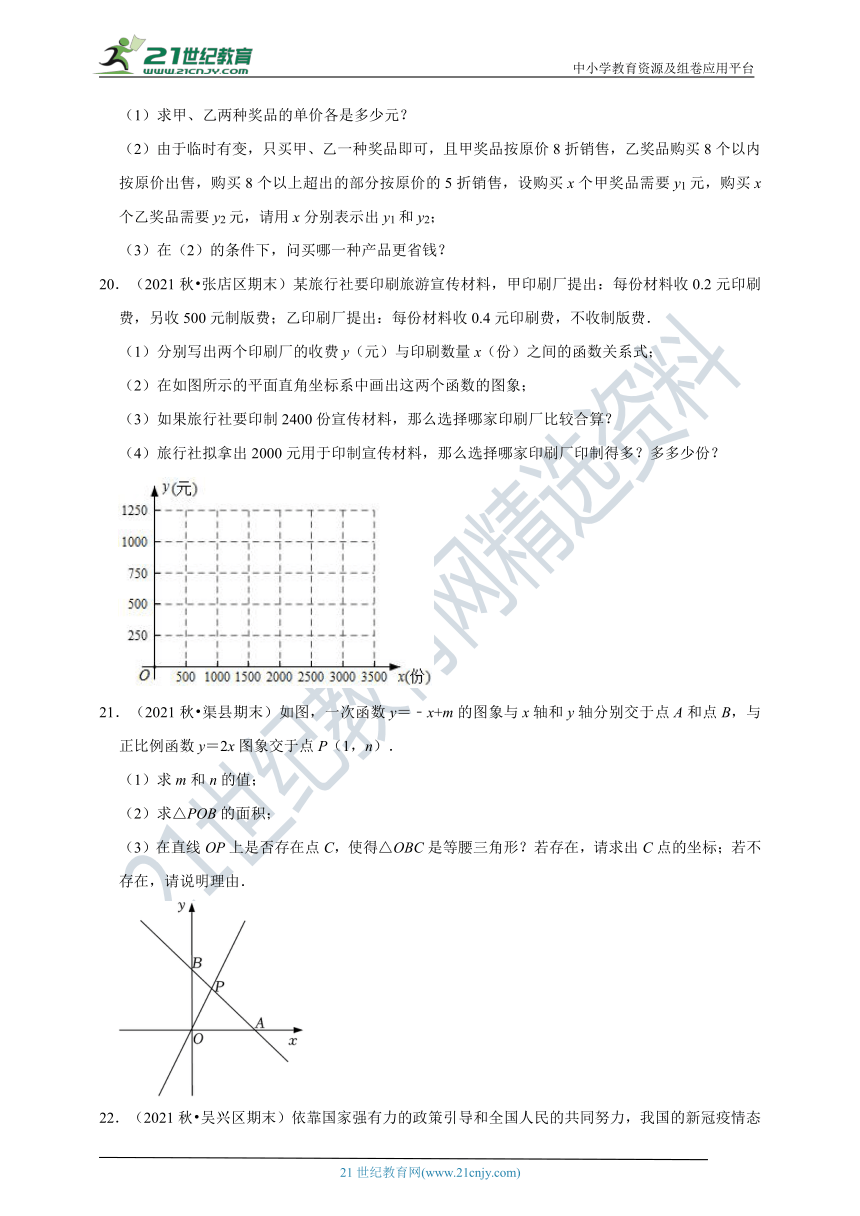
20.(2021秋 张店区期末)某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,另收500元制版费;乙印刷厂提出:每份材料收0.4元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;
(2)在如图所示的平面直角坐标系中画出这两个函数的图象;
(3)如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?
(4)旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?
21.(2021秋 渠县期末)如图,一次函数y=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y=2x图象交于点P(1,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在点C,使得△OBC是等腰三角形?若存在,请求出C点的坐标;若不存在,请说明理由.
22.(2021秋 吴兴区期末)依靠国家强有力的政策引导和全国人民的共同努力,我国的新冠疫情态势得到了有效控制.但当前疫情发展形势依旧严峻,常态化防控工作仍然不能松懈.为了打赢这场没有硝烟的战争,某公司积极响应国家号召,采购了口罩、防护服、消毒剂等医疗物资若干箱,进行物资援助.该公司计划租用某货运公司的A、B型两种货车共6辆完成物资运送,它们的载货量和租金如表:
A B
载货量(箱/辆) 45 30
租金(元/辆) 800 550
设租用A型货车x辆,根据要求回答下列问题:
(1)用含有x的式子填写下表:
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B
(2)若保证租车费用不超过4550元,求x的最大值;
(3)若该公司援助防疫物资共200箱,设这批物资的总运费为y元,求y与x之间的函数关系式,并求出最少运费为多少元?
23.(2020秋 历下区期末)如图,直线l1:y=kx+b与y轴交于点B(0,3),直线l2:y=﹣2x﹣1交y轴于点A,交直线l1于点P(﹣1,t).
(1)求k、b和t的值;
(2)求△ABP的面积;
(3)过动点D(a,0)作x轴的垂线与直线l1、l2,分别交于M、N两点,且MN<4.
①求a的取值范围;
②当△AMP的面积是△AMB的面积的时,求MN的长度.
答案与解析
一.选择题
1.(2021秋 南岸区期末)某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.则y与x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
【解析】解:由题意,得:y=100﹣2(x﹣60)=﹣2x+220,
∴y=﹣2x+220.
故选:C.
2.(2021春 永春县期末)已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
【解析】解:根据三角形的三边关系,得
则0<20﹣2x<2x,
由20﹣2x>0,解得x<10,
由20﹣2x<2x,解得x>5,
则5<x<10.
故选:D.
3.(2021秋 大东区期末)弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
【解析】解:设y与x的关系式为y=kx+b,
∵图象经过(﹣20,0),(20,20),
∴,
解得:,
∴y=x+10,
当x=0时,y=10,
即弹簧不挂物体时的长度是10cm.
故选:B.
4.(2020 西藏)如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
【解析】解:设y与x的函数关系式为y=kx+b,
将点(0,6),(9,10.5)代入上式得,
,
解得,,
即y与x的函数关系式是y=0.5x+6,
当y=7.5时,7.5=0.5x+6,得x=3,
即a的值为3,
故选:A.
5.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的函数图象如图所示,函数关系式为y=kx﹣600,则旅客携带50kg行李时的运费为( )
A.300元 B.500元 C.600元 D.900元
【解析】解:∵y=kx﹣600,点(30,300)在此函数图象上,
∴300=30k﹣600,
解得,k=30,
∴y=30x﹣600,
当x=50时,y=30×50﹣600=900,
即旅客携带50kg行李时的运费为900元,
故选:D.
6.(2021春 乐平市期末)一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米 B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米 D.燃烧10分钟后,剩下蜡烛长度是10厘米
【解析】解:由图象可知,这根蜡烛总长度是15厘米,故选项A不合题意;
由图象可知,燃烧10分钟后剩下蜡烛长度是10厘米,所以燃烧10分所燃烧的长度为5厘米,所以每分钟燃烧0.5厘米,故选项D不合题意,选项C符合题意;
这根蜡烛可燃烧:15÷0.5=30(分钟),故选项B不合题意.
故选:C.
7.(2021秋 济南期中)小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
x ﹣2 ﹣1 0 1
y 6 2 0
A.﹣2 B.0 C.2 D.4
【解析】解:设y=kx+b,
由表格可知,一次函数经过点(0,2),(1,0),
则有,
解得,
∴y=﹣2x+2,
当x=﹣1时,y=4,
故选:D.
8.(2021秋 迎江区校级月考)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,其中结论正确的个数是( )
①汽车在行驶途中停留了0.5h;②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;④汽车出发4h离出发地40km.
A.1 B.2 C.3 D.4
【解析】解:①汽车在行驶途中停留了2﹣1.5=0.5(h),
故①正确;
②平均速度:120×2÷4.5=(千米/小时),
故②错误;
③汽车共行驶了120×2=240(km),
故③正确;
④汽车自出发后3h到4.5h速度为:120÷(4.5﹣3)=120÷1.5=80(千米/小时),
∴汽车出发4h离出发地距离为120﹣(4﹣3)×80=120﹣80=40(千米),
故④正确.
∴正确的是①③④,
故选:C.
9.(2021秋 南岗区校级期末)甲、乙两车分别从相距280km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法:
①乙车的速度是40千米/时; ②甲车从C返回A的速度为70千米/时;
③t=3; ④当两车相距35千米时,乙车行驶的时间是2小时或6小时;
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:由图象可得,乙车的速度为:35÷1=35千米/时,故①错误;
甲车从开始最后回到A地用的时间为:(280﹣35)÷35=7(小时)
则甲从C返回A地的速度为:210÷=70千米/时,故②正确;
由图可得:t==3(小时),故③正确;
乙车行驶的时间是2小时,甲乙相距是280﹣(35×2+70×1)=140千米,故④错误;
故②③正确.
故选:B.
10.(2021春 梁平区期末)张伟骑摩托车从甲地去乙地,李亮开汽车从乙地去甲地,两人同时出发,匀速行驶,各自到达终点后停止,设张伟、李亮两人间的距离为s(单位:千米),张伟行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发3小时时,张伟和李亮同时到达终点;②张伟骑摩托车的速度为千米/小时;
③李亮开汽车的速度为60千米/小时;④出发1.5小时时,李亮比张伟多行驶50千米;
上述结论正确的是( )
A.①② B.③④ C.②④ D.②③④
【解析】解:由图象可得,
在1.5小时时,李亮到达终点,张伟在3小时时到达终点,故①结论错误;
张伟骑摩托车的速度为千米/小时,故②结论正确;
李亮开汽车的速度为:100÷1.5=千米/小时,故③结论错误;
(千米),即出发1.5小时时,李亮比张伟多行驶50千米,故④结论正确,
所以结论正确的是②④.
故选:C.
二.填空题
11.(2020秋 烈山区期中)等腰三角形的周长为16cm,底边长为ycm,腰长为xcm,则y与x之间的关系式为 y=16﹣2x ,自变量x的取值范围为 4<x<8 .
【解析】解:依题意有y=16﹣2x,
又,
解得:4<x<8.
12.(2020春 高州市期中)空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 1721 m.
【解析】解:当x=22时,y=×22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
13.(2021秋 拱墅区月考)一水池蓄水20m3,打开阀门后每小时流出5m3,放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为 Q=20﹣5t ,自变量t的取值范围 0<t≤4 .
【解析】解:放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为:Q=20﹣5t;
20÷5=4(小时),
故自变量t的取值范围为:0<t≤4.
故答案为:Q=20﹣5t;0<t≤4.
14.(2021春 丰台区校级期中)在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 ①②③④ .(填序号)
【解析】解:A、B两地相距=360+80=440(千米),故①正确,
甲车的平均速度==60(千米/小时),故②正确,
乙车的平均速度==40千米/小时,440÷40=11(小时),
∴乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
解得:t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故答案为:①②③④.
15.(2020秋 开江县期末)关于函数y=kx+3+k(k为常数),给出下列结论:①此函数是一次函数;②无论k取什么值,函数图象必经过点(﹣1,3);③若k>0时,函数图象经过第一、二、三象限;④若k<0时,函数图象与x轴的交点始终在负半轴上.其中正确的是 ②③ (填序号).
【解析】解:①当k≠0时,函数y=kx+3+k是一次函数,故①结论错误;
②∵当x=﹣1时,y=kx+3+k=﹣k+3+k=3,
即无论k取何值,该函数图象都经过点点(﹣1,3),故②结论正确;
③若k>0时,y=kx+3+k的图象经过第一、二、三象限,故③结论正确;
④当3+k<0,即k<﹣3时,函数图象与x轴的交点始终在负半轴上,故④结论错误.
综上所述,正确的结论是:②③.
故答案是:②③.
16.(2021秋 锦州期末)平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 22020 .
【解析】解:∵A1(1,1),
∴设A2(2+a,a),则a=(a+2)+,
解得a=2,
∴A2(4,2),
设A3(6+b,b),则有b=(6+b)+,
解得b=4,
∴A3(10,4),
由此发现点An的纵坐标为2n﹣1,
即点A2021的纵坐标是22020,
故答案为:22020.
17.(2020秋 浦东新区校级期末)正比例函数y=kx的图象上一点P到x轴的距离为2,点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,则k的值为 或﹣ .
【解析】解:∵正比例函数y=kx的图象上一点P到x轴的距离为2,
∴|yP|=2,
∵点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,
∴|xP|×2=6,
∴|xP|=6,
∴P(6,2)或P(6,﹣2)或P(﹣6,2)或P(﹣6,﹣2),
当P(6,2)时,2=6k,解得k=,
当P(6,﹣2)时,﹣2=6k,解得k=﹣,
当P(﹣6,2)时,2=﹣6k,解得k=﹣,
当P(﹣6,﹣2)时,﹣2=﹣6k,解得k=,
综上所述,k的值为或﹣,
故答案为:或﹣.
三.解答题
18.(2021秋 任城区期末)我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.
(1)请直接写出y与x之间的函数关系式;
(2)此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃.求飞机离地的高度是多少千米?
【解析】解:(1)由题意可得,
y=30﹣6x,
即y与x之间的函数关系式是y=﹣6x+30;
(2)将y=﹣36代入y=﹣6x+30得,
﹣36=﹣6x+30,
解得x=11,
答:飞机离地的高度是11千米.
19.(2021秋 禅城区期末)学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元;购买甲奖品3个和乙奖品2个,需花费44元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;
(3)在(2)的条件下,问买哪一种产品更省钱?
【解析】解:(1)设甲种奖品的单价为x元/个,乙种奖品的单价为y元/个,
根据题意得:,
解得:.
答:甲种奖品的单价为8元/个,乙种奖品的单价为10元/个.
(2)根据题意得:y1=8×0.8x=6.4x;
当0≤x≤8时,y2=10x,
当x>8时,y2=10×6+10×0.5(x﹣6)=5x+30,
∴y2=;
(3)当0≤x≤8时,
∵6.4<10,
∴此时买甲种产品省钱;
当x>8时,
令y1<y2,则6.4x<5x+30,
解得:x<;
令y1=y2,则6.4x=5x+30,
解得:x=;
令y1>y2,则6.4x>5x+30,
解得:x>.
综上所述:当x≤21时,选择甲种产品更省钱;当x≥22时,选择乙种产品更省钱.
20.(2021秋 张店区期末)某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,另收500元制版费;乙印刷厂提出:每份材料收0.4元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;
(2)在如图所示的平面直角坐标系中画出这两个函数的图象;
(3)如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?
(4)旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?
【解析】解:(1)根据题意得:y甲=0.2x+500,y乙=0.4x;
(2)x=0时,y甲=500,y乙=0;x=2500时,y甲=1000,y乙=1000,描点画出函数图象如下:
(3)选择乙印刷厂比较合算,理由如下:
当x=2400时,甲印刷费为:0.2x+500=980(元),乙印刷费为:0.4x=960(元).
∵980>960,
∴选择乙印刷厂比较合算;
(4)根据(1)中的式子可得:
由0.2x+500=2000,解得x=7500,
由0.4x=2000,解得x=5000,
∵7500﹣5000=2500,
∴选择甲印刷厂印制得多,多2500份.
21.(2021秋 渠县期末)如图,一次函数y=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y=2x图象交于点P(1,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在点C,使得△OBC是等腰三角形?若存在,请求出C点的坐标;若不存在,请说明理由.
【解析】解:(1)∵点P(1,n)在正比例函数y=2x图象上,
∴n=2×1=2,
∴点P的坐标为(1,2).
∵点P(1,2)在一次函数y=﹣x+m的图象上,
∴2=﹣1+m,解得:m=3,
∴一次函数解析式为y=﹣x+3.
∴m的值为3,n的值为2;
(2)当x=0时,y=﹣x+3=3,
∴点B的坐标为(0,3),
∴S△POB=OB xP=×3×1=;
(3)存在.
假设存在满足条件的C点,设其坐标为(t,2t),
则BC2=t2+(3﹣2t)2=5t2﹣12t+9,OC2=t2+(2t)2=5t2,BO=32=9,
∵△OBC为等腰三角形,
∴有OB=OC、BC=BO和BC=OC三种情况,
①当OB=OC时,则5t2=9,解得t=±,此时P点坐标为(,)或(﹣,﹣);
②当BC=BO时,则5t2﹣12t+9=9,解得t=0(舍去)或t=,此时P点坐标为(,);
③当BC=OC时,则5t2﹣12t+9=5t2,解得t=,此时P点坐标为(,);
综上可知存在点C,使得△OBC是等腰三角形,其坐标为(,)或(﹣,﹣)或(,)或(,).
22.(2021秋 吴兴区期末)依靠国家强有力的政策引导和全国人民的共同努力,我国的新冠疫情态势得到了有效控制.但当前疫情发展形势依旧严峻,常态化防控工作仍然不能松懈.为了打赢这场没有硝烟的战争,某公司积极响应国家号召,采购了口罩、防护服、消毒剂等医疗物资若干箱,进行物资援助.该公司计划租用某货运公司的A、B型两种货车共6辆完成物资运送,它们的载货量和租金如表:
A B
载货量(箱/辆) 45 30
租金(元/辆) 800 550
设租用A型货车x辆,根据要求回答下列问题:
(1)用含有x的式子填写下表:
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B 6﹣x 30(6﹣x) 550(6﹣x)
(2)若保证租车费用不超过4550元,求x的最大值;
(3)若该公司援助防疫物资共200箱,设这批物资的总运费为y元,求y与x之间的函数关系式,并求出最少运费为多少元?
【解析】解:(1)由题意可得,
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B 6﹣x 30(6﹣x) 550(6﹣x)
故答案为:6﹣x,30(6﹣x),550(6﹣x);
(2)由题意可知:800x+550(6﹣x)≤4550,
解得x≤5,
∴x的最大值是5;
(3)由题意可得,
y=800x+550(6﹣x)=250x+3300,
∴y随x的增大而增大,
∵45x+30(6﹣x)≥200,
解得x≥,
又∵x为整数,
∴当x=2时,y取得最小值,此时y=3800,
答:y与x之间的函数关系式是y=250x+3300,最少运费为3800元.
23.(2020秋 历下区期末)如图,直线l1:y=kx+b与y轴交于点B(0,3),直线l2:y=﹣2x﹣1交y轴于点A,交直线l1于点P(﹣1,t).
(1)求k、b和t的值;
(2)求△ABP的面积;
(3)过动点D(a,0)作x轴的垂线与直线l1、l2,分别交于M、N两点,且MN<4.
①求a的取值范围;
②当△AMP的面积是△AMB的面积的时,求MN的长度.
【解析】解:(1)∵点P(﹣1,t)在直线直线l2上,
∴t=﹣2×(﹣1)﹣1=1,
即P(﹣1,1),
把B、P的坐标代入可得
,
解得 ,
∴t=1,k=2,b=3;
(2)∵直线y=﹣2x﹣1交y轴于点A,
∴A(0,﹣1),
∵P(﹣1,1),B(0,3),
∴==2;
(3)①∵MN∥y轴,
∴M、N的横坐标为a,
设M、N的纵坐标分别为yM和yN,由(1)可知直线l1的函数表达式为y=2x+3,
∴yM=2a+3,yN=﹣2a﹣1,
当MN在点P左侧时,此时a<﹣1,
则有MN=yN﹣yM=﹣2a﹣1﹣(2a+3)=﹣4a﹣4,
∵MN<4,
∴﹣4a﹣4<4,解得a>﹣2,
∴此时﹣2<a<﹣1;
当MN在点P的右侧时,此时a>﹣1,
则有MN=yM﹣yN=2a+3﹣(﹣2a﹣1)=4a+4,
∵MN<4,
∴4a+4<4,解得a<0,
∴此时﹣1<a<0;
当a=﹣1时,也符合题意,
综上可知当﹣2<a<0时,MN<4;
②由(2)可知S△APB=2,
由题意可知点M只能在y轴的左侧,
当点M在线段BP上时,过点M作MC⊥y轴于点C,如图1
∵S△APM=S△AMB,
∴S△ABM=S△APB=,
∴AB MC=,即2MC=,
解得MC=,
∴点M的横坐标为﹣,即a=﹣,
∴MN=4a+4=﹣+4=;
当点M在线段BP的延长线上时,过点M作MD⊥y轴于点D,如图2,
∵S△APM=,
∴S△ABM=2S△APB=4,
∴AB MD=4,即2MD=4,
解得MD=2,
∴点M的横坐标为﹣2,
∴MN=﹣4a﹣4=8﹣4=4(不合题意舍去),
综上可知MN的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级下 19.3课题学习 选择方案同步练习
一.选择题
1.(2021秋 南岸区期末)某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.则y与x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
2.(2021春 永春县期末)已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
3.(2021秋 大东区期末)弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
4.(2020 西藏)如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
5.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的函数图象如图所示,函数关系式为y=kx﹣600,则旅客携带50kg行李时的运费为( )
A.300元 B.500元 C.600元 D.900元
6.(2021春 乐平市期末)一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米 B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米 D.燃烧10分钟后,剩下蜡烛长度是10厘米
7.(2021秋 济南期中)小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
x ﹣2 ﹣1 0 1
y 6 2 0
A.﹣2 B.0 C.2 D.4
8.(2021秋 迎江区校级月考)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,其中结论正确的个数是( )
①汽车在行驶途中停留了0.5h; ②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;④汽车出发4h离出发地40km.
A.1 B.2 C.3 D.4
9.(2021秋 南岗区校级期末)甲、乙两车分别从相距280km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法:
①乙车的速度是40千米/时; ②甲车从C返回A的速度为70千米/时;
③t=3; ④当两车相距35千米时,乙车行驶的时间是2小时或6小时;
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.(2021春 梁平区期末)张伟骑摩托车从甲地去乙地,李亮开汽车从乙地去甲地,两人同时出发,匀速行驶,各自到达终点后停止,设张伟、李亮两人间的距离为s(单位:千米),张伟行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发3小时时,张伟和李亮同时到达终点;②张伟骑摩托车的速度为千米/小时;
③李亮开汽车的速度为60千米/小时;④出发1.5小时时,李亮比张伟多行驶50千米;
上述结论正确的是( )
A.①② B.③④ C.②④ D.②③④
二.填空题
11.(2020秋 烈山区期中)等腰三角形的周长为16cm,底边长为ycm,腰长为xcm,则y与x之间的关系式为 ,自变量x的取值范围为 .
12.(2020春 高州市期中)空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 m.
13.(2021秋 拱墅区月考)一水池蓄水20m3,打开阀门后每小时流出5m3,放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为 ,自变量t的取值范围 .
14.(2021春 丰台区校级期中)在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 .(填序号)
15.(2020秋 开江县期末)关于函数y=kx+3+k(k为常数),给出下列结论:①此函数是一次函数;②无论k取什么值,函数图象必经过点(﹣1,3);③若k>0时,函数图象经过第一、二、三象限;④若k<0时,函数图象与x轴的交点始终在负半轴上.其中正确的是 (填序号).
16.(2021秋 锦州期末)平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 .
17.(2020秋 浦东新区校级期末)正比例函数y=kx的图象上一点P到x轴的距离为2,点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,则k的值为 .
三.解答题
18.(2021秋 任城区期末)我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.
(1)请直接写出y与x之间的函数关系式;
(2)此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃.求飞机离地的高度是多少千米?
19.(2021秋 禅城区期末)学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元;购买甲奖品3个和乙奖品2个,需花费44元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;
(3)在(2)的条件下,问买哪一种产品更省钱?
20.(2021秋 张店区期末)某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,另收500元制版费;乙印刷厂提出:每份材料收0.4元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;
(2)在如图所示的平面直角坐标系中画出这两个函数的图象;
(3)如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?
(4)旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?
21.(2021秋 渠县期末)如图,一次函数y=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y=2x图象交于点P(1,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在点C,使得△OBC是等腰三角形?若存在,请求出C点的坐标;若不存在,请说明理由.
22.(2021秋 吴兴区期末)依靠国家强有力的政策引导和全国人民的共同努力,我国的新冠疫情态势得到了有效控制.但当前疫情发展形势依旧严峻,常态化防控工作仍然不能松懈.为了打赢这场没有硝烟的战争,某公司积极响应国家号召,采购了口罩、防护服、消毒剂等医疗物资若干箱,进行物资援助.该公司计划租用某货运公司的A、B型两种货车共6辆完成物资运送,它们的载货量和租金如表:
A B
载货量(箱/辆) 45 30
租金(元/辆) 800 550
设租用A型货车x辆,根据要求回答下列问题:
(1)用含有x的式子填写下表:
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B
(2)若保证租车费用不超过4550元,求x的最大值;
(3)若该公司援助防疫物资共200箱,设这批物资的总运费为y元,求y与x之间的函数关系式,并求出最少运费为多少元?
23.(2020秋 历下区期末)如图,直线l1:y=kx+b与y轴交于点B(0,3),直线l2:y=﹣2x﹣1交y轴于点A,交直线l1于点P(﹣1,t).
(1)求k、b和t的值;
(2)求△ABP的面积;
(3)过动点D(a,0)作x轴的垂线与直线l1、l2,分别交于M、N两点,且MN<4.
①求a的取值范围;
②当△AMP的面积是△AMB的面积的时,求MN的长度.
答案与解析
一.选择题
1.(2021秋 南岸区期末)某网店销售一款市场上畅销的护眼台灯,在销售过程中发现,这款护眼台灯销售单价为60元时,每星期卖出100个.如果调整销售单价,每涨价1元,每星期少卖出2个,现网店决定提价销售,设销售单价为x元,每星期销售量为y个.则y与x的函数关系式为( )
A.y=﹣2x+100 B.y=﹣2x+40 C.y=﹣2x+220 D.y=﹣2x+60
【解析】解:由题意,得:y=100﹣2(x﹣60)=﹣2x+220,
∴y=﹣2x+220.
故选:C.
2.(2021春 永春县期末)已知等腰三角形的周长为20cm,底边长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
【解析】解:根据三角形的三边关系,得
则0<20﹣2x<2x,
由20﹣2x>0,解得x<10,
由20﹣2x<2x,解得x>5,
则5<x<10.
故选:D.
3.(2021秋 大东区期末)弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,如图所示,此函数的图象经过A(﹣20,0),B(20,20)两点,则弹簧不挂物体时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
【解析】解:设y与x的关系式为y=kx+b,
∵图象经过(﹣20,0),(20,20),
∴,
解得:,
∴y=x+10,
当x=0时,y=10,
即弹簧不挂物体时的长度是10cm.
故选:B.
4.(2020 西藏)如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
A.3 B.4 C.5 D.6
【解析】解:设y与x的函数关系式为y=kx+b,
将点(0,6),(9,10.5)代入上式得,
,
解得,,
即y与x的函数关系式是y=0.5x+6,
当y=7.5时,7.5=0.5x+6,得x=3,
即a的值为3,
故选:A.
5.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的函数图象如图所示,函数关系式为y=kx﹣600,则旅客携带50kg行李时的运费为( )
A.300元 B.500元 C.600元 D.900元
【解析】解:∵y=kx﹣600,点(30,300)在此函数图象上,
∴300=30k﹣600,
解得,k=30,
∴y=30x﹣600,
当x=50时,y=30×50﹣600=900,
即旅客携带50kg行李时的运费为900元,
故选:D.
6.(2021春 乐平市期末)一根粗细均匀的蜡烛,开始燃烧后,剩下的长度y(厘米)与燃烧的时间x(分钟)的关系如图所示,根据图象得到下列信息,错误的是( )
A.这根蜡烛总长度是15厘米 B.这根蜡烛可燃烧30分钟
C.每分钟燃烧1厘米 D.燃烧10分钟后,剩下蜡烛长度是10厘米
【解析】解:由图象可知,这根蜡烛总长度是15厘米,故选项A不合题意;
由图象可知,燃烧10分钟后剩下蜡烛长度是10厘米,所以燃烧10分所燃烧的长度为5厘米,所以每分钟燃烧0.5厘米,故选项D不合题意,选项C符合题意;
这根蜡烛可燃烧:15÷0.5=30(分钟),故选项B不合题意.
故选:C.
7.(2021秋 济南期中)小明根据某个一次函数关系式填写了如下的表格,其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是( )
x ﹣2 ﹣1 0 1
y 6 2 0
A.﹣2 B.0 C.2 D.4
【解析】解:设y=kx+b,
由表格可知,一次函数经过点(0,2),(1,0),
则有,
解得,
∴y=﹣2x+2,
当x=﹣1时,y=4,
故选:D.
8.(2021秋 迎江区校级月考)如图,折线ABCDE描述了一辆汽车在某一直线上的行驶过程中,汽车离出发地的距离s(km)与行驶时间t(h)之间的函数关系,根据图中提供的信息,其中结论正确的个数是( )
①汽车在行驶途中停留了0.5h;②汽车在整个行驶过程的平均速度是40km/h;
③汽车共行驶了240km;④汽车出发4h离出发地40km.
A.1 B.2 C.3 D.4
【解析】解:①汽车在行驶途中停留了2﹣1.5=0.5(h),
故①正确;
②平均速度:120×2÷4.5=(千米/小时),
故②错误;
③汽车共行驶了120×2=240(km),
故③正确;
④汽车自出发后3h到4.5h速度为:120÷(4.5﹣3)=120÷1.5=80(千米/小时),
∴汽车出发4h离出发地距离为120﹣(4﹣3)×80=120﹣80=40(千米),
故④正确.
∴正确的是①③④,
故选:C.
9.(2021秋 南岗区校级期末)甲、乙两车分别从相距280km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,下列说法:
①乙车的速度是40千米/时; ②甲车从C返回A的速度为70千米/时;
③t=3; ④当两车相距35千米时,乙车行驶的时间是2小时或6小时;
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:由图象可得,乙车的速度为:35÷1=35千米/时,故①错误;
甲车从开始最后回到A地用的时间为:(280﹣35)÷35=7(小时)
则甲从C返回A地的速度为:210÷=70千米/时,故②正确;
由图可得:t==3(小时),故③正确;
乙车行驶的时间是2小时,甲乙相距是280﹣(35×2+70×1)=140千米,故④错误;
故②③正确.
故选:B.
10.(2021春 梁平区期末)张伟骑摩托车从甲地去乙地,李亮开汽车从乙地去甲地,两人同时出发,匀速行驶,各自到达终点后停止,设张伟、李亮两人间的距离为s(单位:千米),张伟行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发3小时时,张伟和李亮同时到达终点;②张伟骑摩托车的速度为千米/小时;
③李亮开汽车的速度为60千米/小时;④出发1.5小时时,李亮比张伟多行驶50千米;
上述结论正确的是( )
A.①② B.③④ C.②④ D.②③④
【解析】解:由图象可得,
在1.5小时时,李亮到达终点,张伟在3小时时到达终点,故①结论错误;
张伟骑摩托车的速度为千米/小时,故②结论正确;
李亮开汽车的速度为:100÷1.5=千米/小时,故③结论错误;
(千米),即出发1.5小时时,李亮比张伟多行驶50千米,故④结论正确,
所以结论正确的是②④.
故选:C.
二.填空题
11.(2020秋 烈山区期中)等腰三角形的周长为16cm,底边长为ycm,腰长为xcm,则y与x之间的关系式为 y=16﹣2x ,自变量x的取值范围为 4<x<8 .
【解析】解:依题意有y=16﹣2x,
又,
解得:4<x<8.
12.(2020春 高州市期中)空气中传播的速度y(m/s)与气温x(℃)之间的关系式为y=x+331;当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为 1721 m.
【解析】解:当x=22时,y=×22+331=344.2,
则当x=22℃时,某人看到烟花燃放5s后才听到声音,则此人与燃放烟花所在地的距离为:344.2×5=1721(m),
故答案为:1721.
13.(2021秋 拱墅区月考)一水池蓄水20m3,打开阀门后每小时流出5m3,放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为 Q=20﹣5t ,自变量t的取值范围 0<t≤4 .
【解析】解:放水后池内剩余的水量Q(m3)与放水时间t(时)的函数关系式为:Q=20﹣5t;
20÷5=4(小时),
故自变量t的取值范围为:0<t≤4.
故答案为:Q=20﹣5t;0<t≤4.
14.(2021春 丰台区校级期中)在A、B两地之间有汽车站C(C在直线AB上),甲车由A地驶往C站,乙车由B地驶往A地,两车同时出发,匀速行驶.甲、乙两车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数图象如图所示,则下列结论:①A、B两地相距440千米;②甲车的平均速度是60千米/时;③乙车行驶11小时后到达A地;④两车行驶4.4小时后相遇,其中正确的结论有是 ①②③④ .(填序号)
【解析】解:A、B两地相距=360+80=440(千米),故①正确,
甲车的平均速度==60(千米/小时),故②正确,
乙车的平均速度==40千米/小时,440÷40=11(小时),
∴乙车行驶11小时后到达A地,故③正确,
设t小时相遇,则有:(60+40)t=440,
解得:t=4.4(小时),
∴两车行驶4.4小时后相遇,故④正确,
故答案为:①②③④.
15.(2020秋 开江县期末)关于函数y=kx+3+k(k为常数),给出下列结论:①此函数是一次函数;②无论k取什么值,函数图象必经过点(﹣1,3);③若k>0时,函数图象经过第一、二、三象限;④若k<0时,函数图象与x轴的交点始终在负半轴上.其中正确的是 ②③ (填序号).
【解析】解:①当k≠0时,函数y=kx+3+k是一次函数,故①结论错误;
②∵当x=﹣1时,y=kx+3+k=﹣k+3+k=3,
即无论k取何值,该函数图象都经过点点(﹣1,3),故②结论正确;
③若k>0时,y=kx+3+k的图象经过第一、二、三象限,故③结论正确;
④当3+k<0,即k<﹣3时,函数图象与x轴的交点始终在负半轴上,故④结论错误.
综上所述,正确的结论是:②③.
故答案是:②③.
16.(2021秋 锦州期末)平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=x+和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),则点A2021的纵坐标是 22020 .
【解析】解:∵A1(1,1),
∴设A2(2+a,a),则a=(a+2)+,
解得a=2,
∴A2(4,2),
设A3(6+b,b),则有b=(6+b)+,
解得b=4,
∴A3(10,4),
由此发现点An的纵坐标为2n﹣1,
即点A2021的纵坐标是22020,
故答案为:22020.
17.(2020秋 浦东新区校级期末)正比例函数y=kx的图象上一点P到x轴的距离为2,点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,则k的值为 或﹣ .
【解析】解:∵正比例函数y=kx的图象上一点P到x轴的距离为2,
∴|yP|=2,
∵点P到x轴的垂线和x轴及该函数图象围成的三角形的面积为6,
∴|xP|×2=6,
∴|xP|=6,
∴P(6,2)或P(6,﹣2)或P(﹣6,2)或P(﹣6,﹣2),
当P(6,2)时,2=6k,解得k=,
当P(6,﹣2)时,﹣2=6k,解得k=﹣,
当P(﹣6,2)时,2=﹣6k,解得k=﹣,
当P(﹣6,﹣2)时,﹣2=﹣6k,解得k=,
综上所述,k的值为或﹣,
故答案为:或﹣.
三.解答题
18.(2021秋 任城区期末)我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,某地地面温度为30℃,设高出地面x千米处的温度为y℃.
(1)请直接写出y与x之间的函数关系式;
(2)此刻,有一架飞机飞过该地上空,若机舱内仪表显示飞机外面的温度为﹣36℃.求飞机离地的高度是多少千米?
【解析】解:(1)由题意可得,
y=30﹣6x,
即y与x之间的函数关系式是y=﹣6x+30;
(2)将y=﹣36代入y=﹣6x+30得,
﹣36=﹣6x+30,
解得x=11,
答:飞机离地的高度是11千米.
19.(2021秋 禅城区期末)学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元;购买甲奖品3个和乙奖品2个,需花费44元.
(1)求甲、乙两种奖品的单价各是多少元?
(2)由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;
(3)在(2)的条件下,问买哪一种产品更省钱?
【解析】解:(1)设甲种奖品的单价为x元/个,乙种奖品的单价为y元/个,
根据题意得:,
解得:.
答:甲种奖品的单价为8元/个,乙种奖品的单价为10元/个.
(2)根据题意得:y1=8×0.8x=6.4x;
当0≤x≤8时,y2=10x,
当x>8时,y2=10×6+10×0.5(x﹣6)=5x+30,
∴y2=;
(3)当0≤x≤8时,
∵6.4<10,
∴此时买甲种产品省钱;
当x>8时,
令y1<y2,则6.4x<5x+30,
解得:x<;
令y1=y2,则6.4x=5x+30,
解得:x=;
令y1>y2,则6.4x>5x+30,
解得:x>.
综上所述:当x≤21时,选择甲种产品更省钱;当x≥22时,选择乙种产品更省钱.
20.(2021秋 张店区期末)某旅行社要印刷旅游宣传材料,甲印刷厂提出:每份材料收0.2元印刷费,另收500元制版费;乙印刷厂提出:每份材料收0.4元印刷费,不收制版费.
(1)分别写出两个印刷厂的收费y(元)与印刷数量x(份)之间的函数关系式;
(2)在如图所示的平面直角坐标系中画出这两个函数的图象;
(3)如果旅行社要印制2400份宣传材料,那么选择哪家印刷厂比较合算?
(4)旅行社拟拿出2000元用于印制宣传材料,那么选择哪家印刷厂印制得多?多多少份?
【解析】解:(1)根据题意得:y甲=0.2x+500,y乙=0.4x;
(2)x=0时,y甲=500,y乙=0;x=2500时,y甲=1000,y乙=1000,描点画出函数图象如下:
(3)选择乙印刷厂比较合算,理由如下:
当x=2400时,甲印刷费为:0.2x+500=980(元),乙印刷费为:0.4x=960(元).
∵980>960,
∴选择乙印刷厂比较合算;
(4)根据(1)中的式子可得:
由0.2x+500=2000,解得x=7500,
由0.4x=2000,解得x=5000,
∵7500﹣5000=2500,
∴选择甲印刷厂印制得多,多2500份.
21.(2021秋 渠县期末)如图,一次函数y=﹣x+m的图象与x轴和y轴分别交于点A和点B,与正比例函数y=2x图象交于点P(1,n).
(1)求m和n的值;
(2)求△POB的面积;
(3)在直线OP上是否存在点C,使得△OBC是等腰三角形?若存在,请求出C点的坐标;若不存在,请说明理由.
【解析】解:(1)∵点P(1,n)在正比例函数y=2x图象上,
∴n=2×1=2,
∴点P的坐标为(1,2).
∵点P(1,2)在一次函数y=﹣x+m的图象上,
∴2=﹣1+m,解得:m=3,
∴一次函数解析式为y=﹣x+3.
∴m的值为3,n的值为2;
(2)当x=0时,y=﹣x+3=3,
∴点B的坐标为(0,3),
∴S△POB=OB xP=×3×1=;
(3)存在.
假设存在满足条件的C点,设其坐标为(t,2t),
则BC2=t2+(3﹣2t)2=5t2﹣12t+9,OC2=t2+(2t)2=5t2,BO=32=9,
∵△OBC为等腰三角形,
∴有OB=OC、BC=BO和BC=OC三种情况,
①当OB=OC时,则5t2=9,解得t=±,此时P点坐标为(,)或(﹣,﹣);
②当BC=BO时,则5t2﹣12t+9=9,解得t=0(舍去)或t=,此时P点坐标为(,);
③当BC=OC时,则5t2﹣12t+9=5t2,解得t=,此时P点坐标为(,);
综上可知存在点C,使得△OBC是等腰三角形,其坐标为(,)或(﹣,﹣)或(,)或(,).
22.(2021秋 吴兴区期末)依靠国家强有力的政策引导和全国人民的共同努力,我国的新冠疫情态势得到了有效控制.但当前疫情发展形势依旧严峻,常态化防控工作仍然不能松懈.为了打赢这场没有硝烟的战争,某公司积极响应国家号召,采购了口罩、防护服、消毒剂等医疗物资若干箱,进行物资援助.该公司计划租用某货运公司的A、B型两种货车共6辆完成物资运送,它们的载货量和租金如表:
A B
载货量(箱/辆) 45 30
租金(元/辆) 800 550
设租用A型货车x辆,根据要求回答下列问题:
(1)用含有x的式子填写下表:
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B 6﹣x 30(6﹣x) 550(6﹣x)
(2)若保证租车费用不超过4550元,求x的最大值;
(3)若该公司援助防疫物资共200箱,设这批物资的总运费为y元,求y与x之间的函数关系式,并求出最少运费为多少元?
【解析】解:(1)由题意可得,
车辆数(辆) 载货量(箱) 租金(元)
A x 45x 800x
B 6﹣x 30(6﹣x) 550(6﹣x)
故答案为:6﹣x,30(6﹣x),550(6﹣x);
(2)由题意可知:800x+550(6﹣x)≤4550,
解得x≤5,
∴x的最大值是5;
(3)由题意可得,
y=800x+550(6﹣x)=250x+3300,
∴y随x的增大而增大,
∵45x+30(6﹣x)≥200,
解得x≥,
又∵x为整数,
∴当x=2时,y取得最小值,此时y=3800,
答:y与x之间的函数关系式是y=250x+3300,最少运费为3800元.
23.(2020秋 历下区期末)如图,直线l1:y=kx+b与y轴交于点B(0,3),直线l2:y=﹣2x﹣1交y轴于点A,交直线l1于点P(﹣1,t).
(1)求k、b和t的值;
(2)求△ABP的面积;
(3)过动点D(a,0)作x轴的垂线与直线l1、l2,分别交于M、N两点,且MN<4.
①求a的取值范围;
②当△AMP的面积是△AMB的面积的时,求MN的长度.
【解析】解:(1)∵点P(﹣1,t)在直线直线l2上,
∴t=﹣2×(﹣1)﹣1=1,
即P(﹣1,1),
把B、P的坐标代入可得
,
解得 ,
∴t=1,k=2,b=3;
(2)∵直线y=﹣2x﹣1交y轴于点A,
∴A(0,﹣1),
∵P(﹣1,1),B(0,3),
∴==2;
(3)①∵MN∥y轴,
∴M、N的横坐标为a,
设M、N的纵坐标分别为yM和yN,由(1)可知直线l1的函数表达式为y=2x+3,
∴yM=2a+3,yN=﹣2a﹣1,
当MN在点P左侧时,此时a<﹣1,
则有MN=yN﹣yM=﹣2a﹣1﹣(2a+3)=﹣4a﹣4,
∵MN<4,
∴﹣4a﹣4<4,解得a>﹣2,
∴此时﹣2<a<﹣1;
当MN在点P的右侧时,此时a>﹣1,
则有MN=yM﹣yN=2a+3﹣(﹣2a﹣1)=4a+4,
∵MN<4,
∴4a+4<4,解得a<0,
∴此时﹣1<a<0;
当a=﹣1时,也符合题意,
综上可知当﹣2<a<0时,MN<4;
②由(2)可知S△APB=2,
由题意可知点M只能在y轴的左侧,
当点M在线段BP上时,过点M作MC⊥y轴于点C,如图1
∵S△APM=S△AMB,
∴S△ABM=S△APB=,
∴AB MC=,即2MC=,
解得MC=,
∴点M的横坐标为﹣,即a=﹣,
∴MN=4a+4=﹣+4=;
当点M在线段BP的延长线上时,过点M作MD⊥y轴于点D,如图2,
∵S△APM=,
∴S△ABM=2S△APB=4,
∴AB MD=4,即2MD=4,
解得MD=2,
∴点M的横坐标为﹣2,
∴MN=﹣4a﹣4=8﹣4=4(不合题意舍去),
综上可知MN的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
