2021-2022学年人教版八年级下 20.2数据的波动程度 同步练习(含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级下 20.2数据的波动程度 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 18:30:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版八年级下 20.2数据的波动程度同步练习
一.选择题
1.(2021秋 东台市期末)一组数据1,﹣1,2,5,3的极差是( )
A.6 B.5 C.4 D.3
2.(2021秋 玄武区期末)一组数据1,2,a,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
3.(2021秋 海阳市期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.(2021秋 新邵县期末)王大伯前几年承包了甲、乙两片荒山,各栽种了100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了四棵杨梅树上的杨梅,每棵的产量如图所示,由统计图提供的信息可知,杨梅产量较稳定的是( )
A.甲山 B.乙山 C.一样 D.无法确定
5.(2021秋 市北区期末)在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,可以看出15表示这组数据的( )
A.众数 B.平均数 C.中位数 D.方差
6.(2021秋 娄星区期末)为了向建党一百周年献礼,某市在中小学中开展了红色经典故事演讲比赛,某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92,关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.方差是72 D.平均数是85
7.(2021秋 南京期末)小明根据演讲比赛中9位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.0 8.2 8.3 0.2
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
8.(2021秋 建宁县期末)若x1,x2,x3, ,xn的平均数为8.方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
9.(2021秋 深圳期末)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
10.(2021 齐齐哈尔二模)一组数据16,m,20,20,24按从小到大的顺序排列,下列选项与m无关的是( )
A.中位数 B.平均数 C.方差 D.众数
二.填空题
11.(2021秋 市中区期末)数据3,3,4,4,6的方差等于 .
12.(2020秋 长兴县月考)若一组数据﹣2,,4,□中,最大的数与最小的数的差是8,则□表示的数是 .
13.(2021秋 聊城期末)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],计算一组数据的方差,那么x1+x2+x3+…+x10= .
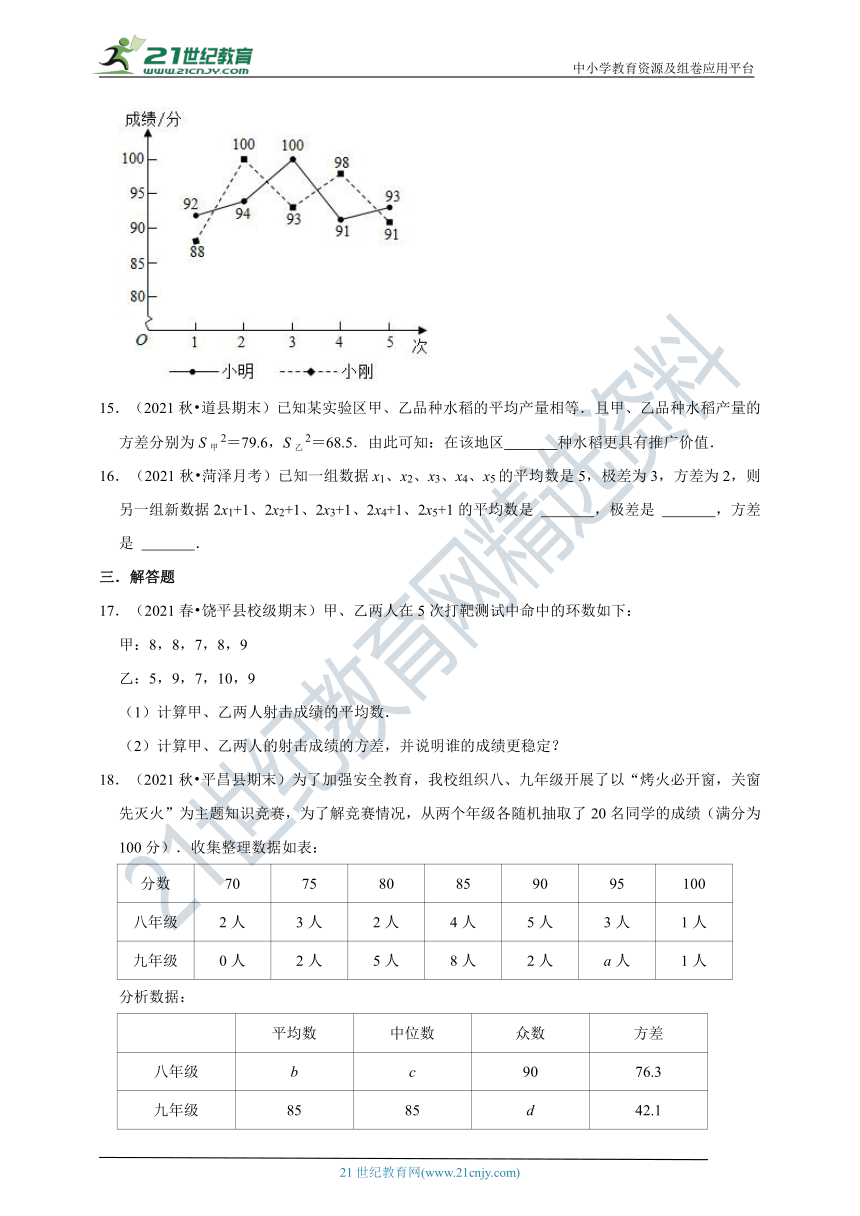
14.(2021秋 东城区校级期末)为庆祝中国共产党建党100周年,某高校组织党史知识竞赛.根据小明、小刚5次预赛成绩绘制成统计图.
下面有三个推断:
①与小刚相比,小明5次成绩的极差大;②与小刚相比,小明5次成绩的方差小;
③与小刚相比,小明的成绩比较稳定. 其中,所有合理推断的序号是 .
15.(2021秋 道县期末)已知某实验区甲、乙品种水稻的平均产量相等.且甲、乙品种水稻产量的方差分别为S甲2=79.6,S乙2=68.5.由此可知:在该地区 种水稻更具有推广价值.
16.(2021秋 菏泽月考)已知一组数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,则另一组新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是 ,极差是 ,方差是 .
三.解答题
17.(2021春 饶平县校级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
18.(2021秋 平昌县期末)为了加强安全教育,我校组织八、九年级开展了以“烤火必开窗,关窗先灭火”为主题知识竞赛,为了解竞赛情况,从两个年级各随机抽取了20名同学的成绩(满分为100分).收集整理数据如表:
分数 70 75 80 85 90 95 100
八年级 2人 3人 2人 4人 5人 3人 1人
九年级 0人 2人 5人 8人 2人 a人 1人
分析数据:
平均数 中位数 众数 方差
八年级 b c 90 76.3
九年级 85 85 d 42.1
根据以上信息回答下列问题:
(1)a= ,b= ,c= ,d= ;
(2)请通过平均数和方差分析两个年级掌握防火知识的情况;
(3)该校八、九年级共有1000人,本次知识竞赛成绩不低于85分的为“优秀”.请估计这两个年级共有多少名学生到达“优秀”.
19.(2021秋 聊城期末)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试类别 平时成绩 期中 期末
测试1 测试2 测试3 测试4 测试5
甲 93 99 100 98 98 96 95
乙 92 93 94 94 95 92 98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数;
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析;
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
20.(2021春 南昌期末)已知:①1,2,3,4,5的平均数是3,方差是2;
②2,3,4,5,6的平均数是4,方差是2;
③1,3,5,7,9的平均数是5,方差是8;
④2,4,6,8,10的平均数是6,方差是8;
请按要求填空:
(1)n,n+1,n+2,n+3,n+4的平均数是 ,方差是 ;
(2)n,n+2,n+4,n+6,n+8的平均数是 ;
(3)n,2n,3n,4n,5n的平均数是 ,方差是 .
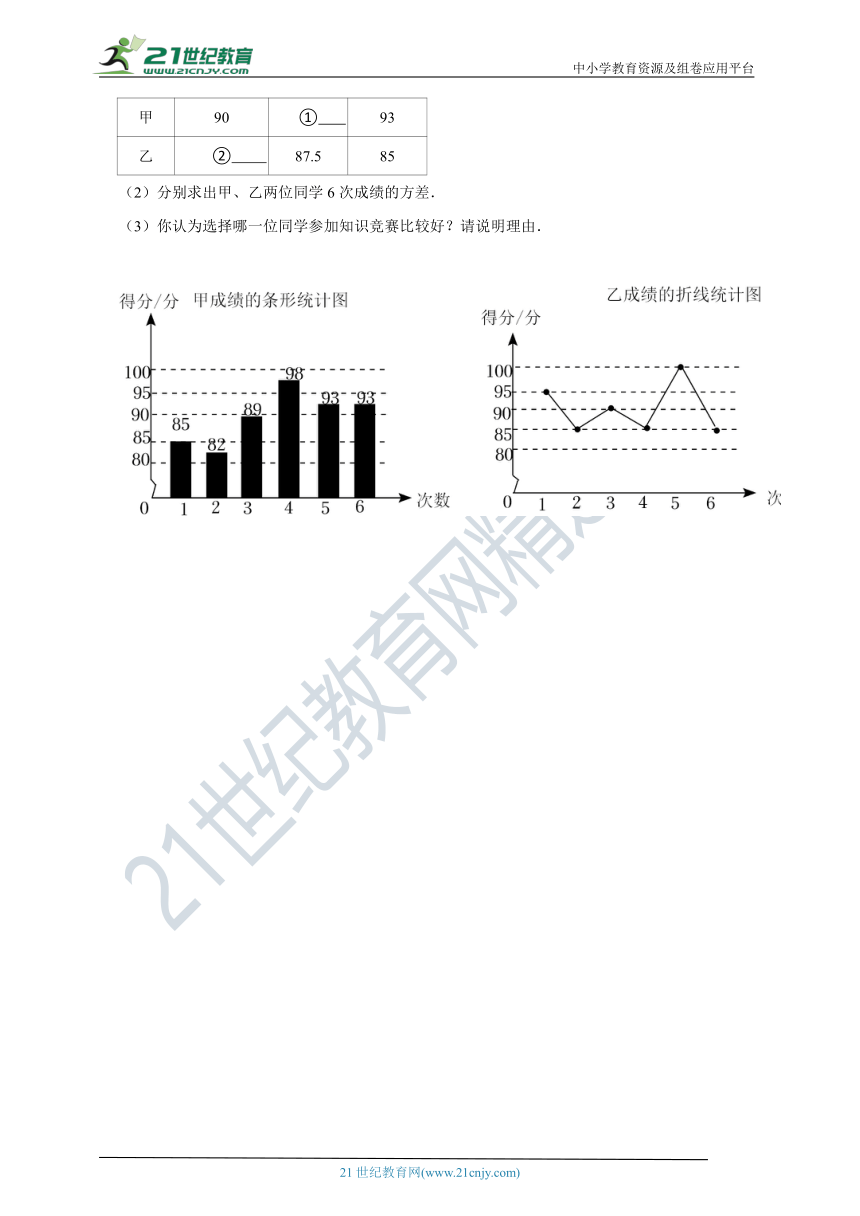
21.(2021秋 玄武区期中)为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)填写下列表格:
平均数/分 中位数/分 众数/分
甲 90 ① 93
乙 ② 87.5 85
(2)分别求出甲、乙两位同学6次成绩的方差.
(3)你认为选择哪一位同学参加知识竞赛比较好?请说明理由.
答案与解析
一.选择题
1.(2021秋 东台市期末)一组数据1,﹣1,2,5,3的极差是( )
A.6 B.5 C.4 D.3
【解析】解:该组数据的极差是:5﹣(﹣1)=6;
故选:A.
2.(2021秋 玄武区期末)一组数据1,2,a,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
【解析】解:根据题意知a=3×4﹣(1+2+3)
=12﹣6
=6,
∴这组数据为1、2、3、6,
∴该组数据的方差为×[(1﹣3)2+(2﹣3)2+(3﹣3)2+(6﹣3)2]=,
故选:B.
3.(2021秋 海阳市期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
【解析】解:∵s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,
∴S乙2<S甲2<S丙2<S丁2,
∴射击成绩最稳定的是乙;
故选:B.
4.(2021秋 新邵县期末)王大伯前几年承包了甲、乙两片荒山,各栽种了100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了四棵杨梅树上的杨梅,每棵的产量如图所示,由统计图提供的信息可知,杨梅产量较稳定的是( )
A.甲山 B.乙山 C.一样 D.无法确定
【解析】解:∵=×(50+36+40+34)=40(千克),=×(36+40+48+36)=40(千克),
S2甲=×[(50 40)2+(36 40)2+(40 40)2+(34 40)2]=38,
S2乙=×[(36﹣40)2+(40﹣40)2+(48﹣40)2+(36﹣40)2]=24,
S2甲>S2乙.
∴乙山上的杨梅产量较稳定,
故选:B.
5.(2021秋 市北区期末)在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,可以看出15表示这组数据的( )
A.众数 B.平均数 C.中位数 D.方差
【解析】解:在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,数15表示这组数据的平均数;
故选:B.
6.(2021秋 娄星区期末)为了向建党一百周年献礼,某市在中小学中开展了红色经典故事演讲比赛,某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92,关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.方差是72 D.平均数是85
【解析】解:将数据重新排列为82,82,83,85,86,92,
A、数据的众数为82,此选项正确,不符合题意;
B、数据的中位数为=84,此选项正确,不符合题意;
C、数据的平均数为=85,
所以方差为×[(85﹣85)2+(83﹣85)2+2×(82﹣85)2+(86﹣85)2+(92﹣85)2]=12,此选项错误,符合题意;
D、由C选项知此选项正确;
故选:C.
7.(2021秋 南京期末)小明根据演讲比赛中9位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.0 8.2 8.3 0.2
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
【解析】解:去掉一个最高分和一个最低分对中位数没有影响,
故选:B.
8.(2021秋 建宁县期末)若x1,x2,x3, ,xn的平均数为8.方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
【解析】解:样本x1+2,x2+2,x3+2,…xn+2,对于样本x1,x2,x3,…xn来说,
每个数据均在原来的基础上增加了2,根据平均数、方差的变化规律得:
平均数较前增加2,而方差不变,即:平均数为8+2=10,方差为2,
故选:C.
9.(2021秋 深圳期末)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
【解析】解:∵甲,乙,丙,丁四个人中丙和丁的平均数最大且相等,
甲,乙,丙,丁四个人中丁的方差最小,
∴综合平均数和方差两个方面说明丁成绩既高又稳定,
∴最合适的人选是丁.
故选:D.
10.(2021 齐齐哈尔二模)一组数据16,m,20,20,24按从小到大的顺序排列,下列选项与m无关的是( )
A.中位数 B.平均数 C.方差 D.众数
【解析】解:组数据16,m,20,20,24按从小到大的顺序排列,当m发生改变时,平均数和众数可能发生变化,方差一定发生变化,中位数不变,
故选:A.
二.填空题
11.(2021秋 市中区期末)数据3,3,4,4,6的方差等于 1.2 .
【解析】解:根据题意,数据3,3,4,4,6,
其平均数=×(3+3+4+4+6)=4,
则其方差s2=[(3﹣4)2+(3﹣4)2+(4﹣4)2+(4﹣4)2+(6﹣4)2]=1.2.
故答案为:1.2.
12.(2020秋 长兴县月考)若一组数据﹣2,,4,□中,最大的数与最小的数的差是8,则□表示的数是 ﹣4或6 .
【解析】解:若□是最大数,则□﹣(﹣2)=8,
解得□=6,
若□是最小数,则4﹣□=8,
解得□=﹣4,
所以,□的值是﹣4或6,
故答案为:﹣4或6.
13.(2021秋 聊城期末)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],计算一组数据的方差,那么x1+x2+x3+…+x10= 30 .
【解析】解:∵S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],
∴平均数为3,共10个数据,
∴x1+x2+x3+…+x10=10×3=30,
故答案为:30.
14.(2021秋 东城区校级期末)为庆祝中国共产党建党100周年,某高校组织党史知识竞赛.根据小明、小刚5次预赛成绩绘制成统计图.
下面有三个推断:
①与小刚相比,小明5次成绩的极差大; ②与小刚相比,小明5次成绩的方差小;
③与小刚相比,小明的成绩比较稳定. 其中,所有合理推断的序号是 ②③ .
【解析】解:小明5次预赛成绩的平均数为:=94(分),
极差为:100﹣91=9(分),
方差为:[(92﹣94)2+(94﹣94)2+(100﹣94)2+(91﹣94)2+(93﹣94)2]=10,
小刚5次预赛成绩的平均数为:=94(分),
极差为:100﹣88=12(分),
方差为:[(88﹣94)2+(100﹣94)2+(93﹣94)2+(98﹣94)2+(91﹣94)2]=19.6,
因此①不正确;②正确;③小明的方差较小,其成绩比较稳定,因此③正确;
所以正确的有:②③,
故答案为:②③.
15.(2021秋 道县期末)已知某实验区甲、乙品种水稻的平均产量相等.且甲、乙品种水稻产量的方差分别为S甲2=79.6,S乙2=68.5.由此可知:在该地区 乙 种水稻更具有推广价值.
【解析】解:根据题意,可得甲、乙两种水稻的平均产量相同,
∵68.5<79.6,
∴S乙2<S甲2,
即乙种水稻的产量稳定,
∴产量稳定,适合推广的品种为乙种水稻.
故答案为:乙
16.(2021秋 菏泽月考)已知一组数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,则另一组新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是 11 ,极差是 6 ,方差是 8 .
【解析】解:∵数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,
∴新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是2×5+1=11,
极差为2×3=6,
方差为2×22=8,
故答案为:11、6、8.
三.解答题
17.(2021春 饶平县校级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
【解析】解:(1)甲射击成绩的平均数=(8+8+7+8+9)=8(环).
乙射击成绩的平均数=(5+9+7+10+9)=8(环).
(2)=(0+0+1+0+1)=0.4;
=(9+1+1+4+1)=3.2;
∵<,
∴甲的成绩更稳定.
18.(2021秋 平昌县期末)为了加强安全教育,我校组织八、九年级开展了以“烤火必开窗,关窗先灭火”为主题知识竞赛,为了解竞赛情况,从两个年级各随机抽取了20名同学的成绩(满分为100分).收集整理数据如表:
分数 70 75 80 85 90 95 100
八年级 2人 3人 2人 4人 5人 3人 1人
九年级 0人 2人 5人 8人 2人 a人 1人
分析数据:
平均数 中位数 众数 方差
八年级 b c 90 76.3
九年级 85 85 d 42.1
根据以上信息回答下列问题:
(1)a= 2 ,b= 85 ,c= 85 ,d= 85 ;
(2)请通过平均数和方差分析两个年级掌握防火知识的情况;
(3)该校八、九年级共有1000人,本次知识竞赛成绩不低于85分的为“优秀”.请估计这两个年级共有多少名学生到达“优秀”.
【解析】解:(1)a=20﹣(0+2+5+8+2+1)=2,
b=×(70×2+75×3+80×2+85×4+90×5+95×3+100×1)=85,
把八年级20名同学的成绩按从小到大的顺序排序,第10,11个数均为85,
∴中位数为c==85,
∵九年级20名同学的成绩中85分出现的次数最多,
∴众数d=85.
故答案为:2,85,85,85;
(2)九年级掌握防火知识的情况更好,理由如下:
八年级和九年级的平均数相同,但九年级方差比八年级小,故九年级成绩更稳定,掌握防火知识的情况更好;
(3)八年级成绩不低于85分的有13人,九年级成绩不低于85分的有13人,
∴1000×=650(名),
即估计这两个年级共有650名学生达到“优秀”.
19.(2021秋 聊城期末)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试类别 平时成绩 期中 期末
测试1 测试2 测试3 测试4 测试5
甲 93 99 100 98 98 96 95
乙 92 93 94 94 95 92 98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数;
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析;
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
【解析】解:(1)把甲学生7次成绩按从小到大的顺序排列为:93,95,96,98,98,99,100,
最中间的数是98,则中位数是98分;
98出现了2次,出现的次数最多,则众数是98分;
(2)甲学生7次成绩的方差是:×[(93﹣97)2+(95﹣97)2+(96﹣97)2+2×(98﹣97)2+(99﹣97)2+(100﹣97)2]=.
乙学生7次成绩的方差是:×[2×(92﹣94)2+(93﹣94)2+2×(94﹣94)2+(95﹣94)2+(98﹣94)2]=.
甲7次成绩的平均分高于乙7次成绩的平均分,但是甲的方差大于乙的方差,说明甲的平均成绩比乙高,但是不如乙的成绩稳定;
(3)甲学生的期末总评成绩是:97.6×40%+96×20%+95×40%=96.24(分),
乙学生的期末总评成绩是:93.6×40%+92×20%+98×40%=95.04(分),
答:甲学生的期末总评成绩是96.24分,乙学生的期末总评成绩是95.04分.
20.(2021春 南昌期末)已知:①1,2,3,4,5的平均数是3,方差是2;
②2,3,4,5,6的平均数是4,方差是2;
③1,3,5,7,9的平均数是5,方差是8;
④2,4,6,8,10的平均数是6,方差是8;
请按要求填空:
(1)n,n+1,n+2,n+3,n+4的平均数是 n+2 ,方差是 2 ;
(2)n,n+2,n+4,n+6,n+8的平均数是 n+4 ;
(3)n,2n,3n,4n,5n的平均数是 3n ,方差是 2n2 .
【解析】解:(1)∵数据n,n+1,n+2,n+3,n+4是在数据1,2,3,4,5的基础上每个数据均加上(n﹣1)所得,
∴数据n,n+1,n+2,n+3,n+4的平均数3+n﹣1=n+2,方差依然是2,
故答案为:n+2,2;
(2)∵数据n,n+2,n+4,n+6,n+8是在数据2,4,6,8,10的基础上每个数据均加上(n﹣2)所得,
∴n,n+2,n+4,n+6,n+8的平均数是6+n﹣2=n+4,
故答案为:n+4;
(3)数据n,2n,3n,4n,5n是将1,2,3,4,5分别乘以n所得,
∴数据n,2n,3n,4n,5n的平均数为3n,方差为2n2,
故答案为:3n,2n2.
21.(2021秋 玄武区期中)为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)填写下列表格:
平均数/分 中位数/分 众数/分
甲 90 ① 91 93
乙 ② 90 87.5 85
(2)分别求出甲、乙两位同学6次成绩的方差.
(3)你认为选择哪一位同学参加知识竞赛比较好?请说明理由.
【解析】解:(1)把这些数从小到大排列为:82,85,89,93,93,98,
则甲同学的中位数是=91(分),
乙同学的平均数是:×(95+85+90+85+100+85)=90(分),
故答案为:91,90;
(2)甲同学的方差是:×[(85﹣90)2+(82﹣90)2+(89﹣90)2+(98﹣90)2+(93﹣90)2+(93﹣90)2]=(分2),
乙同学的方差是:×[(95﹣90)2+(85﹣90)2+(90﹣90)2+(85﹣90)2+(100﹣90)2+(85﹣90)2]=(分2),
(3)选择甲同学.
因为两人的平均数相同,说明两人实力相当,但甲的方差小于乙的方差,说明甲同学发挥更稳定,因此甲同学成绩更优秀,可以选择甲同学参加竞赛.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版八年级下 20.2数据的波动程度同步练习
一.选择题
1.(2021秋 东台市期末)一组数据1,﹣1,2,5,3的极差是( )
A.6 B.5 C.4 D.3
2.(2021秋 玄武区期末)一组数据1,2,a,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
3.(2021秋 海阳市期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4.(2021秋 新邵县期末)王大伯前几年承包了甲、乙两片荒山,各栽种了100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了四棵杨梅树上的杨梅,每棵的产量如图所示,由统计图提供的信息可知,杨梅产量较稳定的是( )
A.甲山 B.乙山 C.一样 D.无法确定
5.(2021秋 市北区期末)在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,可以看出15表示这组数据的( )
A.众数 B.平均数 C.中位数 D.方差
6.(2021秋 娄星区期末)为了向建党一百周年献礼,某市在中小学中开展了红色经典故事演讲比赛,某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92,关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.方差是72 D.平均数是85
7.(2021秋 南京期末)小明根据演讲比赛中9位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.0 8.2 8.3 0.2
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
8.(2021秋 建宁县期末)若x1,x2,x3, ,xn的平均数为8.方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
9.(2021秋 深圳期末)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
10.(2021 齐齐哈尔二模)一组数据16,m,20,20,24按从小到大的顺序排列,下列选项与m无关的是( )
A.中位数 B.平均数 C.方差 D.众数
二.填空题
11.(2021秋 市中区期末)数据3,3,4,4,6的方差等于 .
12.(2020秋 长兴县月考)若一组数据﹣2,,4,□中,最大的数与最小的数的差是8,则□表示的数是 .
13.(2021秋 聊城期末)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],计算一组数据的方差,那么x1+x2+x3+…+x10= .
14.(2021秋 东城区校级期末)为庆祝中国共产党建党100周年,某高校组织党史知识竞赛.根据小明、小刚5次预赛成绩绘制成统计图.
下面有三个推断:
①与小刚相比,小明5次成绩的极差大;②与小刚相比,小明5次成绩的方差小;
③与小刚相比,小明的成绩比较稳定. 其中,所有合理推断的序号是 .
15.(2021秋 道县期末)已知某实验区甲、乙品种水稻的平均产量相等.且甲、乙品种水稻产量的方差分别为S甲2=79.6,S乙2=68.5.由此可知:在该地区 种水稻更具有推广价值.
16.(2021秋 菏泽月考)已知一组数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,则另一组新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是 ,极差是 ,方差是 .
三.解答题
17.(2021春 饶平县校级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
18.(2021秋 平昌县期末)为了加强安全教育,我校组织八、九年级开展了以“烤火必开窗,关窗先灭火”为主题知识竞赛,为了解竞赛情况,从两个年级各随机抽取了20名同学的成绩(满分为100分).收集整理数据如表:
分数 70 75 80 85 90 95 100
八年级 2人 3人 2人 4人 5人 3人 1人
九年级 0人 2人 5人 8人 2人 a人 1人
分析数据:
平均数 中位数 众数 方差
八年级 b c 90 76.3
九年级 85 85 d 42.1
根据以上信息回答下列问题:
(1)a= ,b= ,c= ,d= ;
(2)请通过平均数和方差分析两个年级掌握防火知识的情况;
(3)该校八、九年级共有1000人,本次知识竞赛成绩不低于85分的为“优秀”.请估计这两个年级共有多少名学生到达“优秀”.
19.(2021秋 聊城期末)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试类别 平时成绩 期中 期末
测试1 测试2 测试3 测试4 测试5
甲 93 99 100 98 98 96 95
乙 92 93 94 94 95 92 98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数;
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析;
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
20.(2021春 南昌期末)已知:①1,2,3,4,5的平均数是3,方差是2;
②2,3,4,5,6的平均数是4,方差是2;
③1,3,5,7,9的平均数是5,方差是8;
④2,4,6,8,10的平均数是6,方差是8;
请按要求填空:
(1)n,n+1,n+2,n+3,n+4的平均数是 ,方差是 ;
(2)n,n+2,n+4,n+6,n+8的平均数是 ;
(3)n,2n,3n,4n,5n的平均数是 ,方差是 .
21.(2021秋 玄武区期中)为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)填写下列表格:
平均数/分 中位数/分 众数/分
甲 90 ① 93
乙 ② 87.5 85
(2)分别求出甲、乙两位同学6次成绩的方差.
(3)你认为选择哪一位同学参加知识竞赛比较好?请说明理由.
答案与解析
一.选择题
1.(2021秋 东台市期末)一组数据1,﹣1,2,5,3的极差是( )
A.6 B.5 C.4 D.3
【解析】解:该组数据的极差是:5﹣(﹣1)=6;
故选:A.
2.(2021秋 玄武区期末)一组数据1,2,a,3的平均数是3,则该组数据的方差为( )
A. B. C.6 D.14
【解析】解:根据题意知a=3×4﹣(1+2+3)
=12﹣6
=6,
∴这组数据为1、2、3、6,
∴该组数据的方差为×[(1﹣3)2+(2﹣3)2+(3﹣3)2+(6﹣3)2]=,
故选:B.
3.(2021秋 海阳市期末)甲、乙、丙、丁四人各进行20次射击测试,他们的平均成绩相同,方差分别是s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
【解析】解:∵s甲2=0.8,s乙2=0.6,s丙2=0.9,s丁2=1.0,
∴S乙2<S甲2<S丙2<S丁2,
∴射击成绩最稳定的是乙;
故选:B.
4.(2021秋 新邵县期末)王大伯前几年承包了甲、乙两片荒山,各栽种了100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了四棵杨梅树上的杨梅,每棵的产量如图所示,由统计图提供的信息可知,杨梅产量较稳定的是( )
A.甲山 B.乙山 C.一样 D.无法确定
【解析】解:∵=×(50+36+40+34)=40(千克),=×(36+40+48+36)=40(千克),
S2甲=×[(50 40)2+(36 40)2+(40 40)2+(34 40)2]=38,
S2乙=×[(36﹣40)2+(40﹣40)2+(48﹣40)2+(36﹣40)2]=24,
S2甲>S2乙.
∴乙山上的杨梅产量较稳定,
故选:B.
5.(2021秋 市北区期末)在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,可以看出15表示这组数据的( )
A.众数 B.平均数 C.中位数 D.方差
【解析】解:在方差计算公式s2=[(x1﹣15)2+(x2﹣15)2+…+(x20﹣15)2]中,数15表示这组数据的平均数;
故选:B.
6.(2021秋 娄星区期末)为了向建党一百周年献礼,某市在中小学中开展了红色经典故事演讲比赛,某参赛小组6名同学的成绩(单位:分)分别为:85,82,86,82,83,92,关于这组数据,下列说法错误的是( )
A.众数是82 B.中位数是84 C.方差是72 D.平均数是85
【解析】解:将数据重新排列为82,82,83,85,86,92,
A、数据的众数为82,此选项正确,不符合题意;
B、数据的中位数为=84,此选项正确,不符合题意;
C、数据的平均数为=85,
所以方差为×[(85﹣85)2+(83﹣85)2+2×(82﹣85)2+(86﹣85)2+(92﹣85)2]=12,此选项错误,符合题意;
D、由C选项知此选项正确;
故选:C.
7.(2021秋 南京期末)小明根据演讲比赛中9位评委所给的分数制作了如下表格:
平均数 中位数 众数 方差
8.0 8.2 8.3 0.2
如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
【解析】解:去掉一个最高分和一个最低分对中位数没有影响,
故选:B.
8.(2021秋 建宁县期末)若x1,x2,x3, ,xn的平均数为8.方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
【解析】解:样本x1+2,x2+2,x3+2,…xn+2,对于样本x1,x2,x3,…xn来说,
每个数据均在原来的基础上增加了2,根据平均数、方差的变化规律得:
平均数较前增加2,而方差不变,即:平均数为8+2=10,方差为2,
故选:C.
9.(2021秋 深圳期末)某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙、丁的成绩分析如表所示:
甲 乙 丙 丁
平均数 7.9 7.9 8.0 8.0
方差 3.29 0.49 1.8 0.4
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
【解析】解:∵甲,乙,丙,丁四个人中丙和丁的平均数最大且相等,
甲,乙,丙,丁四个人中丁的方差最小,
∴综合平均数和方差两个方面说明丁成绩既高又稳定,
∴最合适的人选是丁.
故选:D.
10.(2021 齐齐哈尔二模)一组数据16,m,20,20,24按从小到大的顺序排列,下列选项与m无关的是( )
A.中位数 B.平均数 C.方差 D.众数
【解析】解:组数据16,m,20,20,24按从小到大的顺序排列,当m发生改变时,平均数和众数可能发生变化,方差一定发生变化,中位数不变,
故选:A.
二.填空题
11.(2021秋 市中区期末)数据3,3,4,4,6的方差等于 1.2 .
【解析】解:根据题意,数据3,3,4,4,6,
其平均数=×(3+3+4+4+6)=4,
则其方差s2=[(3﹣4)2+(3﹣4)2+(4﹣4)2+(4﹣4)2+(6﹣4)2]=1.2.
故答案为:1.2.
12.(2020秋 长兴县月考)若一组数据﹣2,,4,□中,最大的数与最小的数的差是8,则□表示的数是 ﹣4或6 .
【解析】解:若□是最大数,则□﹣(﹣2)=8,
解得□=6,
若□是最小数,则4﹣□=8,
解得□=﹣4,
所以,□的值是﹣4或6,
故答案为:﹣4或6.
13.(2021秋 聊城期末)小明用S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],计算一组数据的方差,那么x1+x2+x3+…+x10= 30 .
【解析】解:∵S2=[(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2],
∴平均数为3,共10个数据,
∴x1+x2+x3+…+x10=10×3=30,
故答案为:30.
14.(2021秋 东城区校级期末)为庆祝中国共产党建党100周年,某高校组织党史知识竞赛.根据小明、小刚5次预赛成绩绘制成统计图.
下面有三个推断:
①与小刚相比,小明5次成绩的极差大; ②与小刚相比,小明5次成绩的方差小;
③与小刚相比,小明的成绩比较稳定. 其中,所有合理推断的序号是 ②③ .
【解析】解:小明5次预赛成绩的平均数为:=94(分),
极差为:100﹣91=9(分),
方差为:[(92﹣94)2+(94﹣94)2+(100﹣94)2+(91﹣94)2+(93﹣94)2]=10,
小刚5次预赛成绩的平均数为:=94(分),
极差为:100﹣88=12(分),
方差为:[(88﹣94)2+(100﹣94)2+(93﹣94)2+(98﹣94)2+(91﹣94)2]=19.6,
因此①不正确;②正确;③小明的方差较小,其成绩比较稳定,因此③正确;
所以正确的有:②③,
故答案为:②③.
15.(2021秋 道县期末)已知某实验区甲、乙品种水稻的平均产量相等.且甲、乙品种水稻产量的方差分别为S甲2=79.6,S乙2=68.5.由此可知:在该地区 乙 种水稻更具有推广价值.
【解析】解:根据题意,可得甲、乙两种水稻的平均产量相同,
∵68.5<79.6,
∴S乙2<S甲2,
即乙种水稻的产量稳定,
∴产量稳定,适合推广的品种为乙种水稻.
故答案为:乙
16.(2021秋 菏泽月考)已知一组数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,则另一组新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是 11 ,极差是 6 ,方差是 8 .
【解析】解:∵数据x1、x2、x3、x4、x5的平均数是5,极差为3,方差为2,
∴新数据2x1+1、2x2+1、2x3+1、2x4+1、2x5+1的平均数是2×5+1=11,
极差为2×3=6,
方差为2×22=8,
故答案为:11、6、8.
三.解答题
17.(2021春 饶平县校级期末)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)计算甲、乙两人射击成绩的平均数.
(2)计算甲、乙两人的射击成绩的方差,并说明谁的成绩更稳定?
【解析】解:(1)甲射击成绩的平均数=(8+8+7+8+9)=8(环).
乙射击成绩的平均数=(5+9+7+10+9)=8(环).
(2)=(0+0+1+0+1)=0.4;
=(9+1+1+4+1)=3.2;
∵<,
∴甲的成绩更稳定.
18.(2021秋 平昌县期末)为了加强安全教育,我校组织八、九年级开展了以“烤火必开窗,关窗先灭火”为主题知识竞赛,为了解竞赛情况,从两个年级各随机抽取了20名同学的成绩(满分为100分).收集整理数据如表:
分数 70 75 80 85 90 95 100
八年级 2人 3人 2人 4人 5人 3人 1人
九年级 0人 2人 5人 8人 2人 a人 1人
分析数据:
平均数 中位数 众数 方差
八年级 b c 90 76.3
九年级 85 85 d 42.1
根据以上信息回答下列问题:
(1)a= 2 ,b= 85 ,c= 85 ,d= 85 ;
(2)请通过平均数和方差分析两个年级掌握防火知识的情况;
(3)该校八、九年级共有1000人,本次知识竞赛成绩不低于85分的为“优秀”.请估计这两个年级共有多少名学生到达“优秀”.
【解析】解:(1)a=20﹣(0+2+5+8+2+1)=2,
b=×(70×2+75×3+80×2+85×4+90×5+95×3+100×1)=85,
把八年级20名同学的成绩按从小到大的顺序排序,第10,11个数均为85,
∴中位数为c==85,
∵九年级20名同学的成绩中85分出现的次数最多,
∴众数d=85.
故答案为:2,85,85,85;
(2)九年级掌握防火知识的情况更好,理由如下:
八年级和九年级的平均数相同,但九年级方差比八年级小,故九年级成绩更稳定,掌握防火知识的情况更好;
(3)八年级成绩不低于85分的有13人,九年级成绩不低于85分的有13人,
∴1000×=650(名),
即估计这两个年级共有650名学生达到“优秀”.
19.(2021秋 聊城期末)表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
测试类别 平时成绩 期中 期末
测试1 测试2 测试3 测试4 测试5
甲 93 99 100 98 98 96 95
乙 92 93 94 94 95 92 98
请你完成下列问题:
(1)请求出甲学生7次成绩的中位数、众数;
(2)已知甲7次成绩的平均分是97分,乙7次成绩的平均分是94分,请求出甲、乙两名学生7次成绩的方差,并根据计算后的方差及两人的平均成绩,对两人成绩进行比较分析;
(3)已知甲平时成绩的平均分是97.6分,乙平时成绩的平均分是93.6分,学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,这两名学生的期末总评成绩是多少?
【解析】解:(1)把甲学生7次成绩按从小到大的顺序排列为:93,95,96,98,98,99,100,
最中间的数是98,则中位数是98分;
98出现了2次,出现的次数最多,则众数是98分;
(2)甲学生7次成绩的方差是:×[(93﹣97)2+(95﹣97)2+(96﹣97)2+2×(98﹣97)2+(99﹣97)2+(100﹣97)2]=.
乙学生7次成绩的方差是:×[2×(92﹣94)2+(93﹣94)2+2×(94﹣94)2+(95﹣94)2+(98﹣94)2]=.
甲7次成绩的平均分高于乙7次成绩的平均分,但是甲的方差大于乙的方差,说明甲的平均成绩比乙高,但是不如乙的成绩稳定;
(3)甲学生的期末总评成绩是:97.6×40%+96×20%+95×40%=96.24(分),
乙学生的期末总评成绩是:93.6×40%+92×20%+98×40%=95.04(分),
答:甲学生的期末总评成绩是96.24分,乙学生的期末总评成绩是95.04分.
20.(2021春 南昌期末)已知:①1,2,3,4,5的平均数是3,方差是2;
②2,3,4,5,6的平均数是4,方差是2;
③1,3,5,7,9的平均数是5,方差是8;
④2,4,6,8,10的平均数是6,方差是8;
请按要求填空:
(1)n,n+1,n+2,n+3,n+4的平均数是 n+2 ,方差是 2 ;
(2)n,n+2,n+4,n+6,n+8的平均数是 n+4 ;
(3)n,2n,3n,4n,5n的平均数是 3n ,方差是 2n2 .
【解析】解:(1)∵数据n,n+1,n+2,n+3,n+4是在数据1,2,3,4,5的基础上每个数据均加上(n﹣1)所得,
∴数据n,n+1,n+2,n+3,n+4的平均数3+n﹣1=n+2,方差依然是2,
故答案为:n+2,2;
(2)∵数据n,n+2,n+4,n+6,n+8是在数据2,4,6,8,10的基础上每个数据均加上(n﹣2)所得,
∴n,n+2,n+4,n+6,n+8的平均数是6+n﹣2=n+4,
故答案为:n+4;
(3)数据n,2n,3n,4n,5n是将1,2,3,4,5分别乘以n所得,
∴数据n,2n,3n,4n,5n的平均数为3n,方差为2n2,
故答案为:3n,2n2.
21.(2021秋 玄武区期中)为了从甲、乙两位同学中选拔一人参加知识竞赛,举行了6次选拔赛,根据两位同学6次选拔赛的成绩,分别绘制了如图统计图.
(1)填写下列表格:
平均数/分 中位数/分 众数/分
甲 90 ① 91 93
乙 ② 90 87.5 85
(2)分别求出甲、乙两位同学6次成绩的方差.
(3)你认为选择哪一位同学参加知识竞赛比较好?请说明理由.
【解析】解:(1)把这些数从小到大排列为:82,85,89,93,93,98,
则甲同学的中位数是=91(分),
乙同学的平均数是:×(95+85+90+85+100+85)=90(分),
故答案为:91,90;
(2)甲同学的方差是:×[(85﹣90)2+(82﹣90)2+(89﹣90)2+(98﹣90)2+(93﹣90)2+(93﹣90)2]=(分2),
乙同学的方差是:×[(95﹣90)2+(85﹣90)2+(90﹣90)2+(85﹣90)2+(100﹣90)2+(85﹣90)2]=(分2),
(3)选择甲同学.
因为两人的平均数相同,说明两人实力相当,但甲的方差小于乙的方差,说明甲同学发挥更稳定,因此甲同学成绩更优秀,可以选择甲同学参加竞赛.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
