2022年华师大版七年级数学下册6.2.1.2方程的简单变形课件(16张)
文档属性
| 名称 | 2022年华师大版七年级数学下册6.2.1.2方程的简单变形课件(16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 475.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 19:00:30 | ||
图片预览





文档简介
(共16张PPT)
6.2 解一元一次方程
第2课时 方程的简单变形
6.2.1 等式的性质与方程的简单变形
复习引入
等式性质1:
等式两边同时加(或减)同一个数(或式),所得结果仍是等式.
即,如果a = b,那么
a +c= b+c,a-c=b-c .
等式两边同时乘(或除以)同一个数(或式)(除数或除式不能为0),所得结果仍是等式.
等式性质2:
ac=bc,
即,如果a = b,那么
新知讲解
☆ 一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做
一元一次方程.
注意以下三点:
(1)一元一次方程有如下特点:①只含有一个未
知数; ②未知数的次数是1;③分母中没有未知数。
(2)一元一次方程的最简形式为:ax=b(a≠0)。
(3)一元一次方程的标准形式为:ax+b= 0
(其中x是未知数,a、b是已知数,并且(a≠0)。
例题精讲
1、下列各式是一元一次方程的是( )
B
(A) (B)
(C) (D)
2、已知 是一元一次方程,则m= .
0
新知讲解
规则1:
方程两边同时加(或减)同一个数或同一个整式,方程的解不变.
方程两边同时乘(或除以)同一个不等于0的数,方程的解不变.
规则2:
☆ 方程的变形规则:
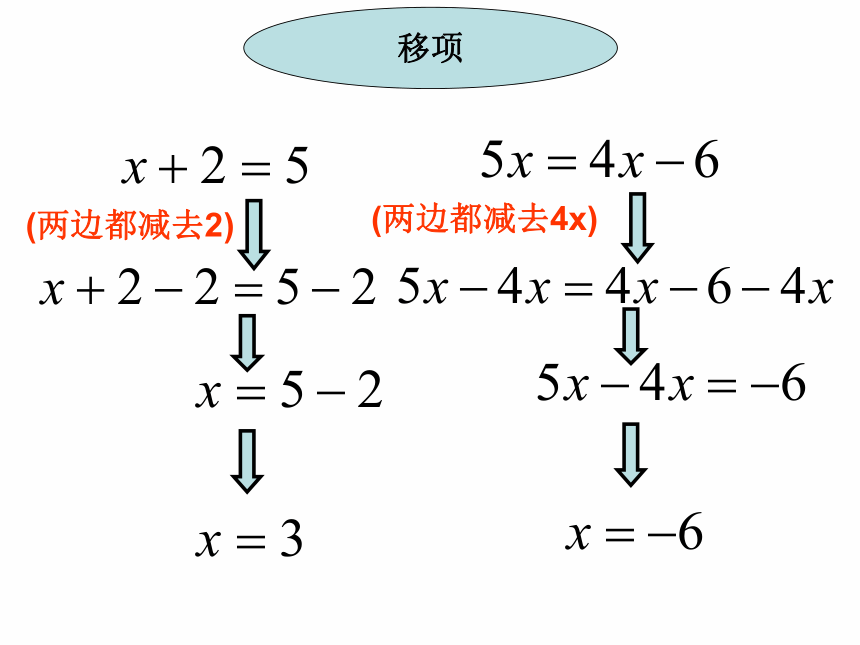
(两边都减去2)
(两边都减去4x)
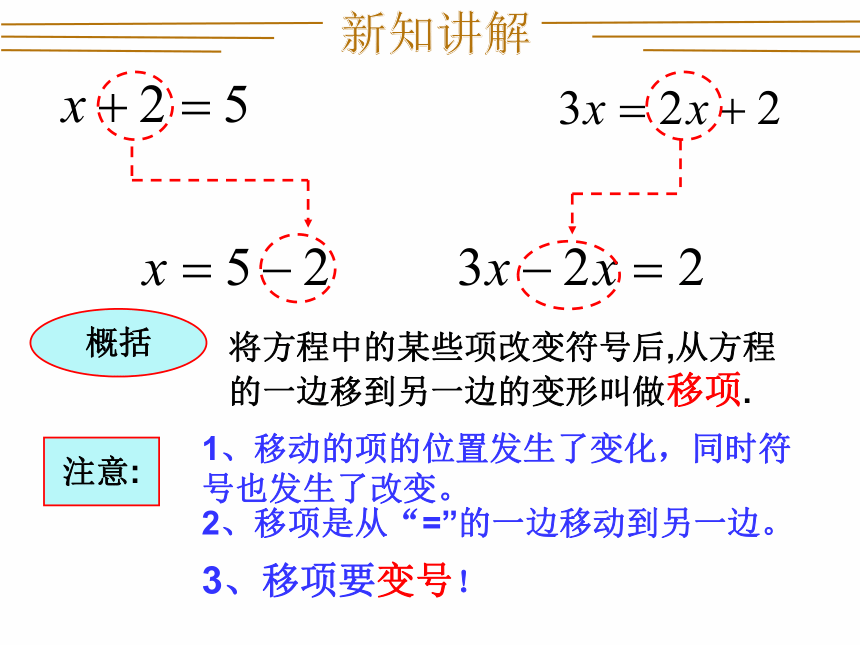
移项
新知讲解
概括
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.
注意:
3、移项要变号!
1、移动的项的位置发生了变化,同时符号也发生了改变。
2、移项是从“=”的一边移动到另一边。
例题精讲
(1)5+x=10移项得x= 10+5 ;
(2)6x=2x+8移项得 6x+2x =8;
(3)5-2x=4-3x移项得3x-2x=4-5;
(4)-2x+7=1-8x移项得-2x+8x=1-7.
×
×
√
√
10-5
6x-2x
下面的移项对不对?如果不对,应怎样改正?
(如何变形 )
(两边都除以2)
将未知数的系数化为1
化系数为“1”
新知讲解
请运用等式的性质解下列方程
(1)4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x= 9+15.
2x -5x = -21.
练习一
书本P7练习1,2
1.
新知讲解
2.
解:
新知讲解
练习二
书本P8练习1
当堂训练
1、已知 是一元一次方程,则m = 。
0
2、解下列方程:
课堂小结
(1)一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
(2)移项的依据是等式的性质1.
2.移项
3.解形如“ax+b=cx+d”的方程的一般步骤:
(1)移项;(2)合并同类项;(3)化未知数的系数为1.
1.一元一次方程
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做
谢谢观看
6.2 解一元一次方程
第2课时 方程的简单变形
6.2.1 等式的性质与方程的简单变形
复习引入
等式性质1:
等式两边同时加(或减)同一个数(或式),所得结果仍是等式.
即,如果a = b,那么
a +c= b+c,a-c=b-c .
等式两边同时乘(或除以)同一个数(或式)(除数或除式不能为0),所得结果仍是等式.
等式性质2:
ac=bc,
即,如果a = b,那么
新知讲解
☆ 一元一次方程定义:
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做
一元一次方程.
注意以下三点:
(1)一元一次方程有如下特点:①只含有一个未
知数; ②未知数的次数是1;③分母中没有未知数。
(2)一元一次方程的最简形式为:ax=b(a≠0)。
(3)一元一次方程的标准形式为:ax+b= 0
(其中x是未知数,a、b是已知数,并且(a≠0)。
例题精讲
1、下列各式是一元一次方程的是( )
B
(A) (B)
(C) (D)
2、已知 是一元一次方程,则m= .
0
新知讲解
规则1:
方程两边同时加(或减)同一个数或同一个整式,方程的解不变.
方程两边同时乘(或除以)同一个不等于0的数,方程的解不变.
规则2:
☆ 方程的变形规则:
(两边都减去2)
(两边都减去4x)
移项
新知讲解
概括
将方程中的某些项改变符号后,从方程的一边移到另一边的变形叫做移项.
注意:
3、移项要变号!
1、移动的项的位置发生了变化,同时符号也发生了改变。
2、移项是从“=”的一边移动到另一边。
例题精讲
(1)5+x=10移项得x= 10+5 ;
(2)6x=2x+8移项得 6x+2x =8;
(3)5-2x=4-3x移项得3x-2x=4-5;
(4)-2x+7=1-8x移项得-2x+8x=1-7.
×
×
√
√
10-5
6x-2x
下面的移项对不对?如果不对,应怎样改正?
(如何变形 )
(两边都除以2)
将未知数的系数化为1
化系数为“1”
新知讲解
请运用等式的性质解下列方程
(1)4x - 15 = 9
解:两边都减去 5x ,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
4x – 15 = 9
+ 15
+ 15
–5x
–5x
4x= 9+15.
2x -5x = -21.
练习一
书本P7练习1,2
1.
新知讲解
2.
解:
新知讲解
练习二
书本P8练习1
当堂训练
1、已知 是一元一次方程,则m = 。
0
2、解下列方程:
课堂小结
(1)一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
(2)移项的依据是等式的性质1.
2.移项
3.解形如“ax+b=cx+d”的方程的一般步骤:
(1)移项;(2)合并同类项;(3)化未知数的系数为1.
1.一元一次方程
只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数是1,这样的方程叫做
谢谢观看
