2022年人教版七年级数学 下册 5.3.1 平行线的性质 课件(共28张)
文档属性
| 名称 | 2022年人教版七年级数学 下册 5.3.1 平行线的性质 课件(共28张) |  | |
| 格式 | zip | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 22:15:00 | ||
图片预览




文档简介
(共28张PPT)
平行线判定的知识点回顾
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
上节课通过同位角、内错角、同旁内角
之间的关系证明平行线的过程,
这节课我们学习已知两直线平行,
同位角、内错角、同旁内角存在什么关系?
5.3 平行线的性质
第五章 相交线与平行线
导入新课
讲授新课
当堂练习
课堂小结
5.3.1 平行线的性质
学习目标
1、理解平行线的性质。
2、能初步运用平行线的性质进行有关计算。
3、体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力。
重点
平行线性质的研究和探索。
难点
正确区分平行线的性质和判定。
前 言
a
b
c
1
3
2
4
8
5
7
6
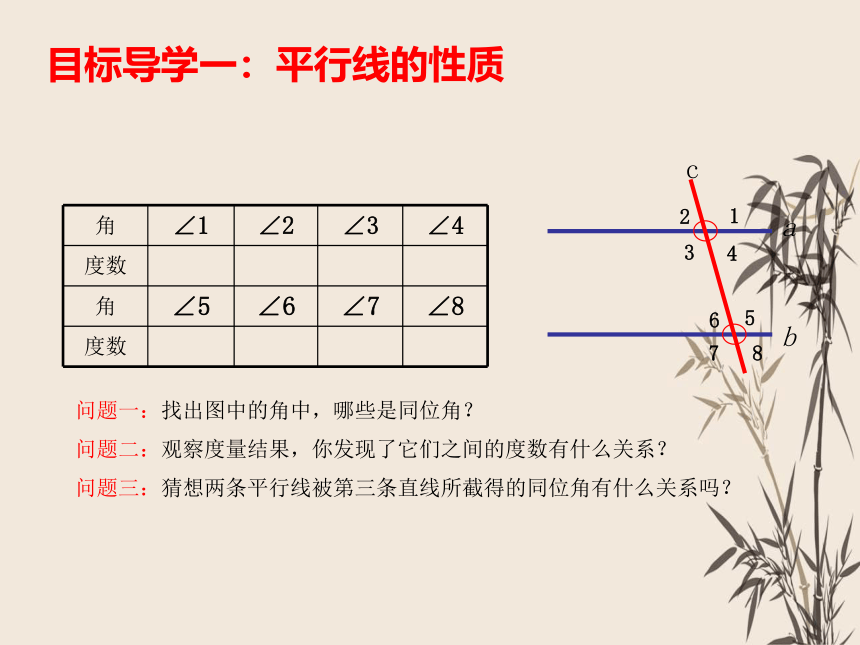
问题一:找出图中的角中,哪些是同位角?
问题二:观察度量结果,你发现了它们之间的度数有什么关系?
问题三:猜想两条平行线被第三条直线所截得的同位角有什么关系吗?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
目标导学一:平行线的性质
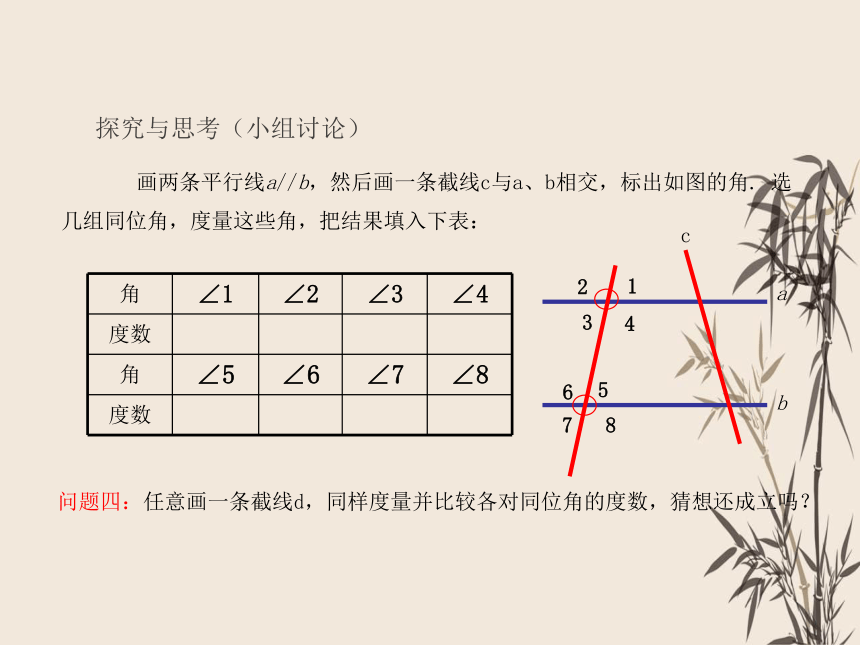
探究与思考(小组讨论)
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 选几组同位角,度量这些角,把结果填入下表:
a
b
c
1
3
2
4
8
5
7
6
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
问题四:任意画一条截线d,同样度量并比较各对同位角的度数,猜想还成立吗?
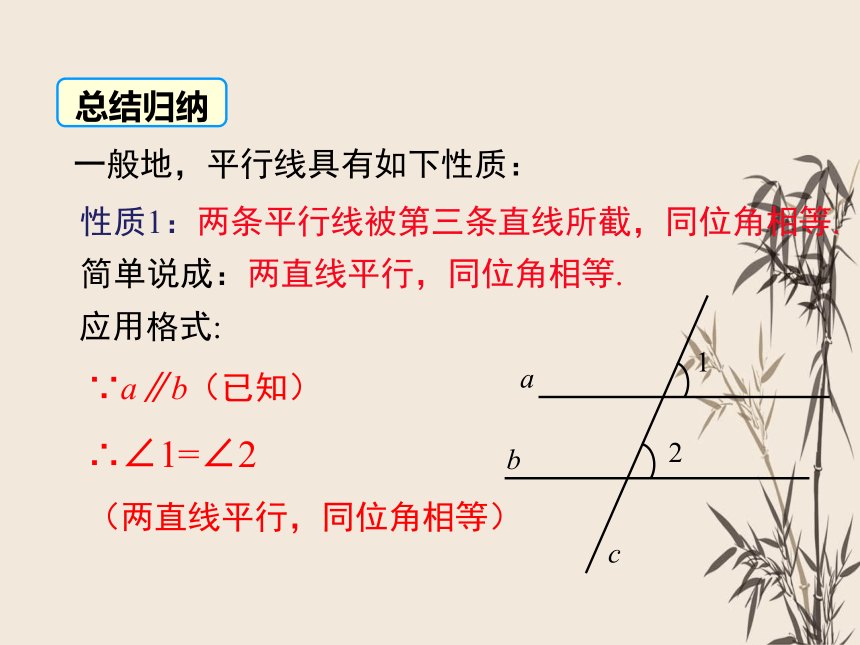
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
总结归纳
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么内错角之间有什么关系呢
∵ a∥b(已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2=∠3 (对顶角相等)
∴ ∠1=∠3(等量代换)
如图,已知a∥b ,试证明∠1与∠3之间的关系.
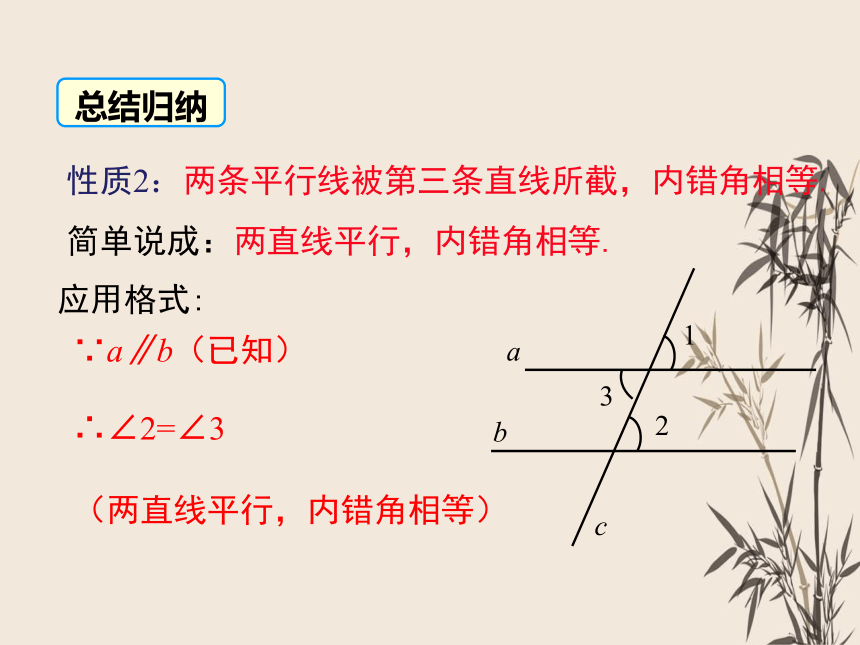
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
a
b
c
1
2
A
B
3
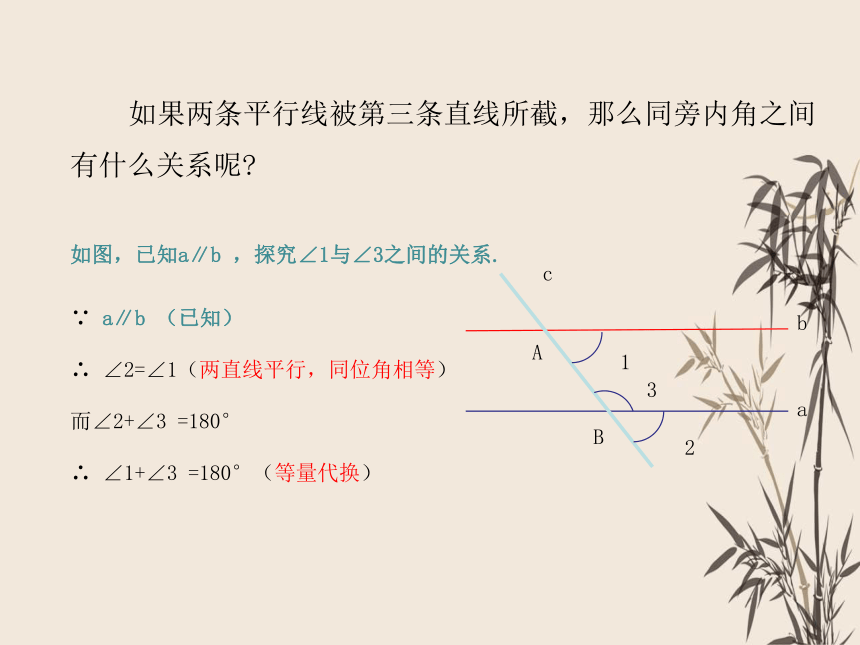
如果两条平行线被第三条直线所截,那么同旁内角之间有什么关系呢
∵ a∥b (已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2+∠3 =180°
∴ ∠1+∠3 =180°(等量代换)
如图,已知a∥b ,探究∠1与∠3之间的关系.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
总结归纳
平行线的性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简而言之:两直线平行,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
简而言之:两直线平行,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简而言之:两直线平行,同旁内角互补.
性质1:∵a∥b(已知),
∴ ∠1 =∠5 (两直线平行,同位角相等).
性质2:∵a∥b(已知),
∴ ∠3 =∠5 (两直线平行,内错角相等).
性质3:∵a∥b(已知),
∴ ∠3+∠6=180°(两直线平行,同旁内角互补).
符号语言:(不唯一)
c
1
2
3
4
a
b
d
5
6
7
8
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
平行线的判定与性质
例1:如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?
D
C
A
B
解:∵梯形两底边AB∥CD,
∴∠D=180°-∠A=180°-100°=80°,
∠C=180°-∠B=180°-115°=65°.
目标导学二:平行线的性质和判定及其综合应用
反馈练习:
一块梯形铁片的残余部分如图,量得∠A=75°, ∠B=72°,梯形的另外两个角分别是多少度?
解:∵梯形两底边AB∥CD,
∴∠D=180°-∠A=180°-75°=105°,
∠C=180°-∠B=180°-72°=108°.
D
C
A
B
例2.已知:如图,∠ABC和∠ACB的平分线交于点O,EF经过点O且平行于BC,分别与AB,AC交于点E,F.∠ABC=50°,∠ACB=60°,求∠BOC的度数。
解:∵OB平分∠ABC,OC平分∠ACB
∠ABC=50°,∠ACB=60°(已知)
∴∠OBC=ABC=25°,∠OCB= ACB=30°(角平分线的性质)
∵EF∥BC(已知)
∴∠1=∠OBC,∠2=∠OCB(两直线平行,内错角相等)
∵∠1+∠2+∠BOC=180°(平角的定义)
∴∠BOC=180°-25°-30°=125°
1
2
我们知道“三角形三个内角的和为180°”,现在我们利用平行线的性质来证明这个结论是正确的。
例3.已知:如图,∠BAC,∠B,∠C是三角形ABC的三个内角。
求证:∠BAC+∠B+∠C=180°
证明:过点A作直线DE∥BC(请你把证明过程补充完整)
A
C
B
E
D
∵DE∥BC(已知)
∴∠B=∠BAD,∠C=∠CAE
(两直线平行,内错角相等)
∵∠BAD+∠BAC+∠CAE=180°(平角的定义)
∴∠B+∠BAC+∠C=180°(等量代换)
潜望镜的原理
如图,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时, ∠1=∠2 、∠3=∠4 ,说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.
画两条平行线,说出你画图的根据;再任意画一条直线和这两条平行线都相交,写出所成的角当中的一对内错角,并说明这一对内错角相等的理由.
b
2
a
c
3
解:如图,a∥b,
根据:利用同位角相等,两直线平行画图;
∠3和∠2是内错角, ∠3=∠2,
理由:两直线平行,内错角相等.
即学即练
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
1.如图,直线被所截,且,则下列结论中正确的是( )
A. B.
C. D.
【答案】B
【详解】如图,∵a//b,
∴∠1=∠5,∠3=∠4,
∵∠2+∠5=180°,∴无法得到∠2=∠5,即得不到∠1=∠2,
由已知得不到 、,
所以正确的只有B选项,
故选B.
检测目标
2.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )
A.50° B.45° C.30° D.40°
【答案】D
【详解】
解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:D.
检测目标
3.如图,已知CD∥BE, 如果∠1=60°, 那么∠B的度数为( )
A.70° B.100° C.110° D.120°
【答案】D
【详解】
解:∵∠1=60°,
∴∠2=180°- 60°=120°.
∵CD∥BE,
∴∠2=∠B=120°.
故选:D.
检测目标
4.如图,AB∥CD,则,,则的大小是( )
A. B. C. D.
【答案】B
【详解】
∵∠DEC=100°,∠C=40°,
∴∠D=180°-∠DEC-∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
检测目标
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
5.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
平行线判定的知识点回顾
平行线判定方法1:
平行线判定方法2:
平行线判定方法3:
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
上节课通过同位角、内错角、同旁内角
之间的关系证明平行线的过程,
这节课我们学习已知两直线平行,
同位角、内错角、同旁内角存在什么关系?
5.3 平行线的性质
第五章 相交线与平行线
导入新课
讲授新课
当堂练习
课堂小结
5.3.1 平行线的性质
学习目标
1、理解平行线的性质。
2、能初步运用平行线的性质进行有关计算。
3、体会“观察-猜想-证明”的探索方法,培养学生辩证和逻辑能力。
重点
平行线性质的研究和探索。
难点
正确区分平行线的性质和判定。
前 言
a
b
c
1
3
2
4
8
5
7
6
问题一:找出图中的角中,哪些是同位角?
问题二:观察度量结果,你发现了它们之间的度数有什么关系?
问题三:猜想两条平行线被第三条直线所截得的同位角有什么关系吗?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
目标导学一:平行线的性质
探究与思考(小组讨论)
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图的角. 选几组同位角,度量这些角,把结果填入下表:
a
b
c
1
3
2
4
8
5
7
6
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
问题四:任意画一条截线d,同样度量并比较各对同位角的度数,猜想还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
总结归纳
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么内错角之间有什么关系呢
∵ a∥b(已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2=∠3 (对顶角相等)
∴ ∠1=∠3(等量代换)
如图,已知a∥b ,试证明∠1与∠3之间的关系.
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
a
b
c
1
2
A
B
3
如果两条平行线被第三条直线所截,那么同旁内角之间有什么关系呢
∵ a∥b (已知)
∴ ∠2=∠1(两直线平行,同位角相等)
而∠2+∠3 =180°
∴ ∠1+∠3 =180°(等量代换)
如图,已知a∥b ,探究∠1与∠3之间的关系.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
总结归纳
平行线的性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简而言之:两直线平行,同位角相等.
性质2:两条平行线被第三条直线所截,内错角相等.
简而言之:两直线平行,内错角相等.
性质3:两条平行线被第三条直线所截,同旁内角互补.
简而言之:两直线平行,同旁内角互补.
性质1:∵a∥b(已知),
∴ ∠1 =∠5 (两直线平行,同位角相等).
性质2:∵a∥b(已知),
∴ ∠3 =∠5 (两直线平行,内错角相等).
性质3:∵a∥b(已知),
∴ ∠3+∠6=180°(两直线平行,同旁内角互补).
符号语言:(不唯一)
c
1
2
3
4
a
b
d
5
6
7
8
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
平行线的判定与性质
例1:如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形另外两个角分别是多少度?
D
C
A
B
解:∵梯形两底边AB∥CD,
∴∠D=180°-∠A=180°-100°=80°,
∠C=180°-∠B=180°-115°=65°.
目标导学二:平行线的性质和判定及其综合应用
反馈练习:
一块梯形铁片的残余部分如图,量得∠A=75°, ∠B=72°,梯形的另外两个角分别是多少度?
解:∵梯形两底边AB∥CD,
∴∠D=180°-∠A=180°-75°=105°,
∠C=180°-∠B=180°-72°=108°.
D
C
A
B
例2.已知:如图,∠ABC和∠ACB的平分线交于点O,EF经过点O且平行于BC,分别与AB,AC交于点E,F.∠ABC=50°,∠ACB=60°,求∠BOC的度数。
解:∵OB平分∠ABC,OC平分∠ACB
∠ABC=50°,∠ACB=60°(已知)
∴∠OBC=ABC=25°,∠OCB= ACB=30°(角平分线的性质)
∵EF∥BC(已知)
∴∠1=∠OBC,∠2=∠OCB(两直线平行,内错角相等)
∵∠1+∠2+∠BOC=180°(平角的定义)
∴∠BOC=180°-25°-30°=125°
1
2
我们知道“三角形三个内角的和为180°”,现在我们利用平行线的性质来证明这个结论是正确的。
例3.已知:如图,∠BAC,∠B,∠C是三角形ABC的三个内角。
求证:∠BAC+∠B+∠C=180°
证明:过点A作直线DE∥BC(请你把证明过程补充完整)
A
C
B
E
D
∵DE∥BC(已知)
∴∠B=∠BAD,∠C=∠CAE
(两直线平行,内错角相等)
∵∠BAD+∠BAC+∠CAE=180°(平角的定义)
∴∠B+∠BAC+∠C=180°(等量代换)
潜望镜的原理
如图,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射时, ∠1=∠2 、∠3=∠4 ,说明为什么进入潜望镜的光线和离开潜望镜的光线是平行的.
画两条平行线,说出你画图的根据;再任意画一条直线和这两条平行线都相交,写出所成的角当中的一对内错角,并说明这一对内错角相等的理由.
b
2
a
c
3
解:如图,a∥b,
根据:利用同位角相等,两直线平行画图;
∠3和∠2是内错角, ∠3=∠2,
理由:两直线平行,内错角相等.
即学即练
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
1.如图,直线被所截,且,则下列结论中正确的是( )
A. B.
C. D.
【答案】B
【详解】如图,∵a//b,
∴∠1=∠5,∠3=∠4,
∵∠2+∠5=180°,∴无法得到∠2=∠5,即得不到∠1=∠2,
由已知得不到 、,
所以正确的只有B选项,
故选B.
检测目标
2.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2的度数为( )
A.50° B.45° C.30° D.40°
【答案】D
【详解】
解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:D.
检测目标
3.如图,已知CD∥BE, 如果∠1=60°, 那么∠B的度数为( )
A.70° B.100° C.110° D.120°
【答案】D
【详解】
解:∵∠1=60°,
∴∠2=180°- 60°=120°.
∵CD∥BE,
∴∠2=∠B=120°.
故选:D.
检测目标
4.如图,AB∥CD,则,,则的大小是( )
A. B. C. D.
【答案】B
【详解】
∵∠DEC=100°,∠C=40°,
∴∠D=180°-∠DEC-∠C=40°,
又∵AB∥CD,
∴∠B=∠D=40°,
故选B.
检测目标
∴∠ABD=∠BDC(两直线平行,内错角相等)
证明:∵AB∥CD(已知)
∵AE∥BD( 已知)
∴∠BDC=∠E (两直线平行,同位角相等)
∴∠ABD=∠E(等量代换)
5.如图,已知:AB∥CD,AE∥BD,试说明∠ABD=∠E.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
