2022年人教版七年级数学 下册7.1.2 平面直角坐标系 课件(共38张)
文档属性
| 名称 | 2022年人教版七年级数学 下册7.1.2 平面直角坐标系 课件(共38张) |

|
|
| 格式 | zip | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-10 22:25:24 | ||
图片预览






文档简介
(共38张PPT)
如何确定直线上点的位置?
在直线上规定了原点、正方向、单位长
就构成了数轴。
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
A
B
类似于利用数轴确定直线上的点的位置的方法,能否找到一种方法来确定平面内的点的位置呢? (点A,B,C,D.)
平面上确定一个点的位置的方法
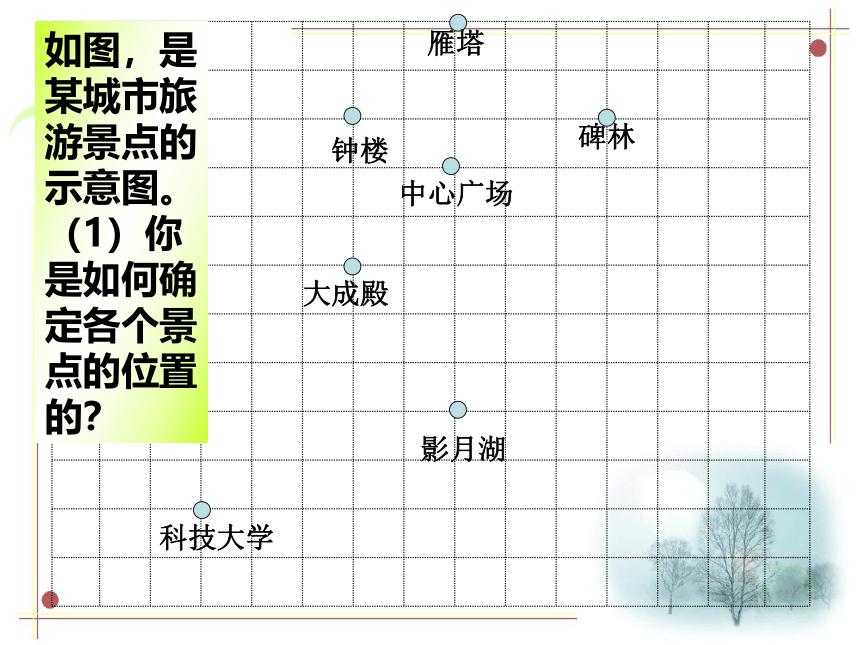
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图。(1)你是如何确定各个景点的位置的?
你知道吗?
法国数学家笛卡儿----法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,引入坐标系,用代数方法解决几何问题。
1596--1650
导入新课
讲授新课
当堂练习
课堂小结
7.1 平面直角坐标系
第七章 平面直角坐标系
7.1.2 平面直角坐标系
1.理解平面直角坐标系以及横轴、纵轴、原点、坐
标等概念,认识并能画出平面直角坐标系;
2. 理解各象限内及坐标轴上点的坐标特征;(重点)
3.会用象限或坐标轴说明直角坐标系内点的位置,
能根据横、纵坐标的符号确定点的位置.(难点)
学习目标
认真阅读课本中7.1.2 平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
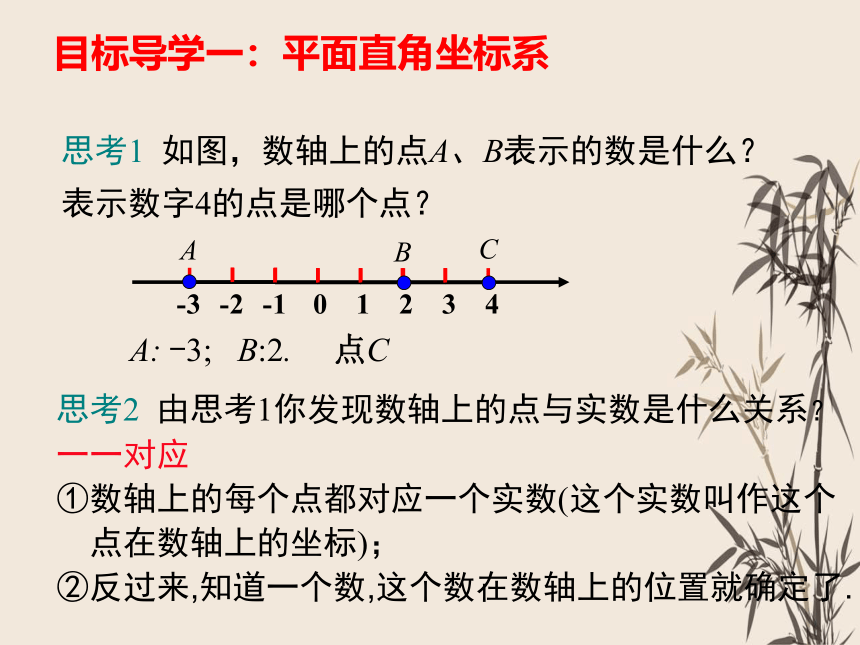
思考1 如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
思考2 由思考1你发现数轴上的点与实数是什么关系?
一一对应
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
A: -3; B:2.
点C
目标导学一:平面直角坐标系
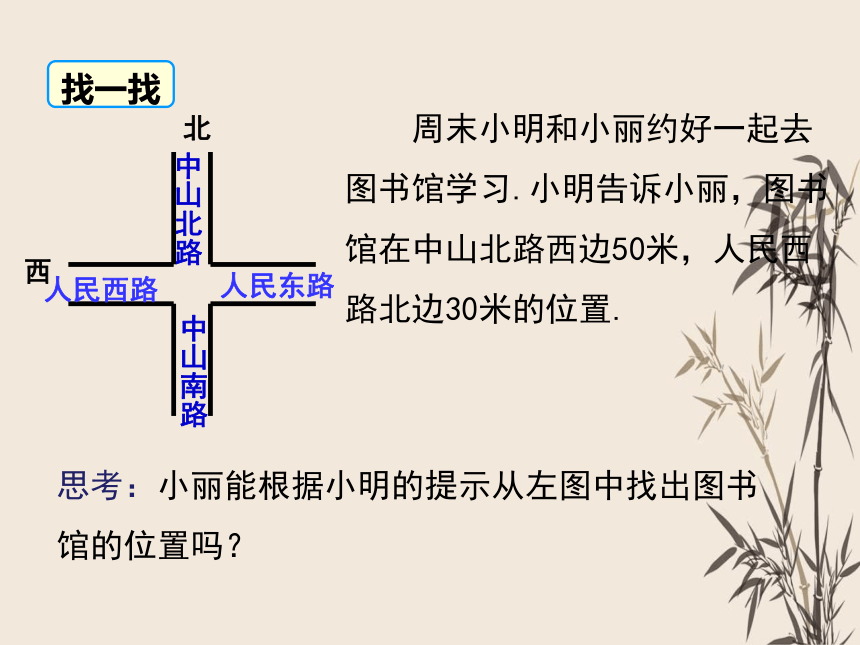
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
中山南路
人民东路
中山北路
人民西路
北
西
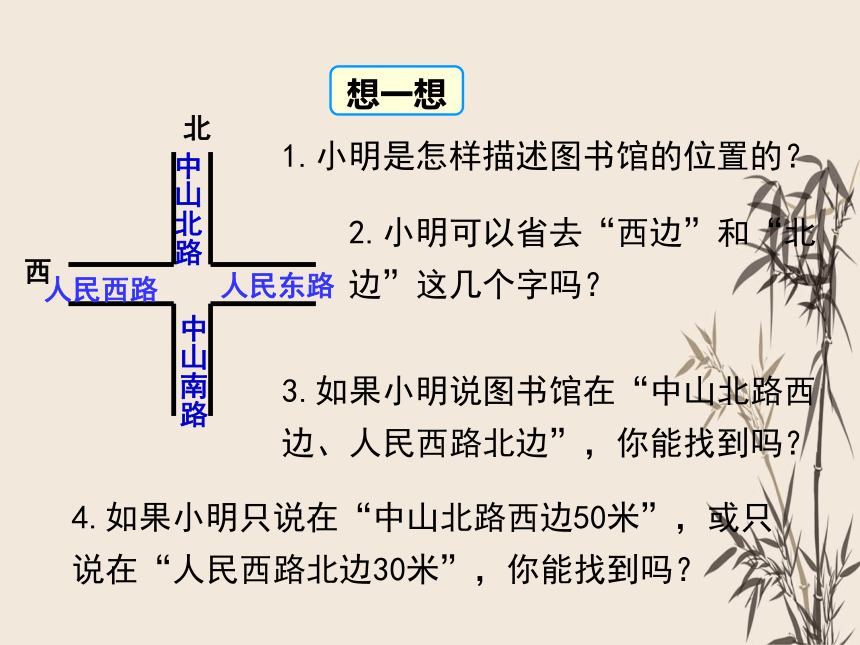
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
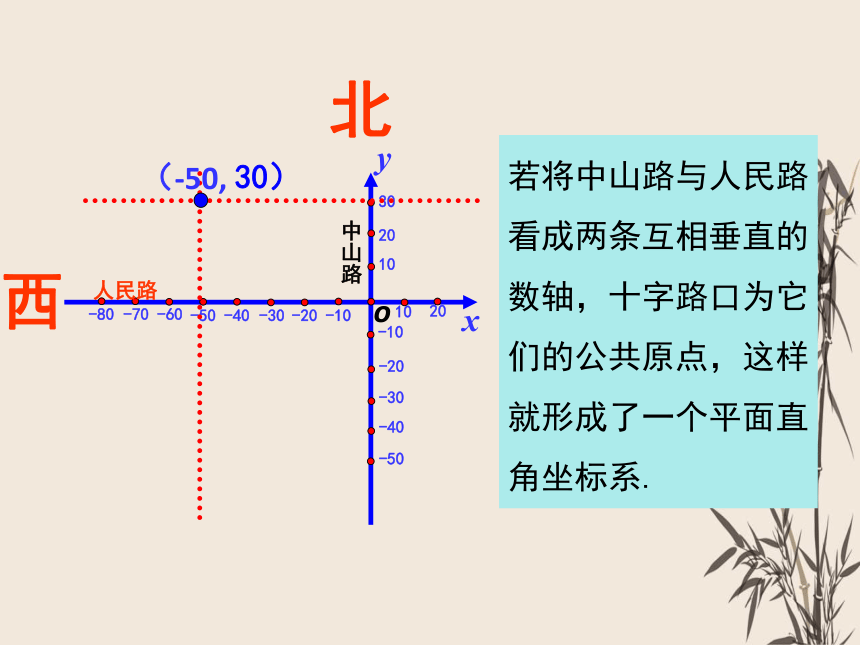
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
x轴
横轴
y轴
纵轴
直角坐标
系的原点
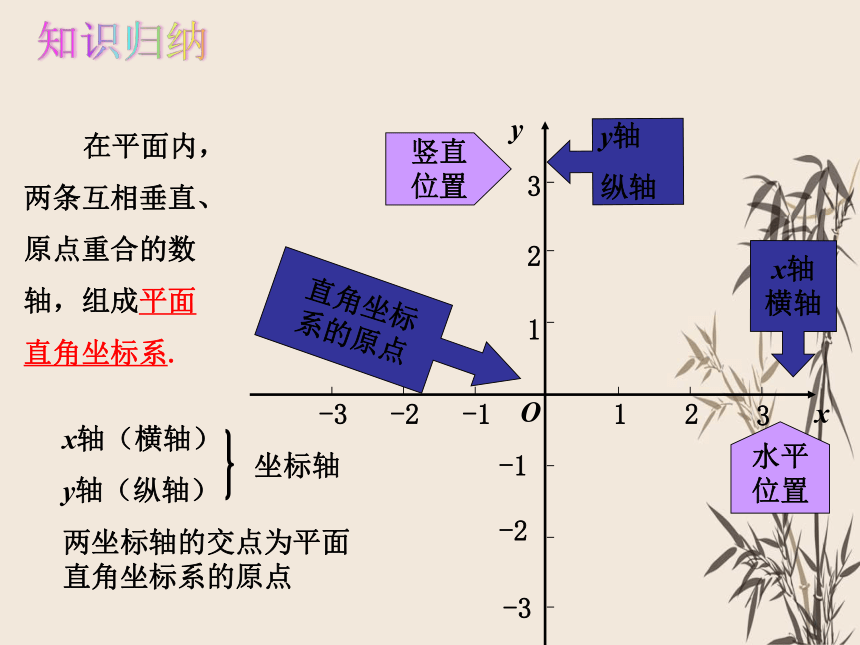
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
知识归纳
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点在平面直角坐标系中的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
知识归纳
平面直角坐标系中两条数轴特征:
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
x
O
下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
即学即练
平面上点的表示。
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
O
X
Y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
例1.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
已知坐标平面内的点,说出它的坐标.
如图:说出A,B,C,D,M,N各点的坐标.
-4 –3 –2 –1 O
1 2 3 4 5
-1
-2
-3
-4
x
y
●
●
1
2
3
4
●
●
●
●
A
(3,4)
B
C
D
N
M
(-3,-4)
(0,2)
(0,-3)
(3,0)
(0,4)
即学即练
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
目标导学二:直角坐标系中点的坐标的特征
探究各坐标轴上、象限内的点的特征.
(1)各坐标轴上的点的坐标有什么特征?
(2)各象限内的点的符号有什么特点?
合作探究
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,
-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
合作探究
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
特殊位置的点的符号特征:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
问题.坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例2
例3:长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
方法总结:由已知条件正确确定坐标轴的位置是解决本题的关键.
目标导学三:建立坐标系求图形中点的坐标
建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
【总结】建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
课堂小结
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
1.在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1)
C.(-3,-5) D.(3,-5)
D
检测目标
2.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
B
检测目标
3.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( )
A原点 Bx轴正半轴
C第一象限 D任意位置
B
检测目标
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴
(B)平行于y轴
(C)经过原点
(D)以上都不对
B
检测目标
5.如果在y轴上,那么点P的坐标是( )
A. B.
C. D.
【答案】B
【详解】
解:∵在y轴上,
∴解得,
∴点P的坐标是(0,-2).故选B.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
如何确定直线上点的位置?
在直线上规定了原点、正方向、单位长
就构成了数轴。
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
·
单位长度
0
1
2
3
4
-3
-2
-1
原点
A
B
类似于利用数轴确定直线上的点的位置的方法,能否找到一种方法来确定平面内的点的位置呢? (点A,B,C,D.)
平面上确定一个点的位置的方法
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图。(1)你是如何确定各个景点的位置的?
你知道吗?
法国数学家笛卡儿----法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,引入坐标系,用代数方法解决几何问题。
1596--1650
导入新课
讲授新课
当堂练习
课堂小结
7.1 平面直角坐标系
第七章 平面直角坐标系
7.1.2 平面直角坐标系
1.理解平面直角坐标系以及横轴、纵轴、原点、坐
标等概念,认识并能画出平面直角坐标系;
2. 理解各象限内及坐标轴上点的坐标特征;(重点)
3.会用象限或坐标轴说明直角坐标系内点的位置,
能根据横、纵坐标的符号确定点的位置.(难点)
学习目标
认真阅读课本中7.1.2 平面直角坐标系的内容,完成下面任务。
自主研学
学习任务:
1.如何确定一个点在数轴上的位置.
2.平面直角坐标系的概念,如何建立平面直角坐标系,象限划分.
思考1 如图,数轴上的点A、B表示的数是什么?
表示数字4的点是哪个点?
0
1
2
3
4
-3
-2
-1
A
B
C
思考2 由思考1你发现数轴上的点与实数是什么关系?
一一对应
①数轴上的每个点都对应一个实数(这个实数叫作这个
点在数轴上的坐标);
②反过来,知道一个数,这个数在数轴上的位置就确定了.
A: -3; B:2.
点C
目标导学一:平面直角坐标系
思考:小丽能根据小明的提示从左图中找出图书馆的位置吗?
周末小明和小丽约好一起去图书馆学习.小明告诉小丽,图书馆在中山北路西边50米,人民西路北边30米的位置.
中山南路
人民东路
中山北路
人民西路
北
西
找一找
中山南路
人民东路
中山北路
人民西路
北
西
想一想
4.如果小明只说在“中山北路西边50米”,或只说在“人民西路北边30米”,你能找到吗?
1.小明是怎样描述图书馆的位置的?
2.小明可以省去“西边”和“北边”这几个字吗?
3.如果小明说图书馆在“中山北路西边、人民西路北边”,你能找到吗?
若将中山路与人民路看成两条互相垂直的数轴,十字路口为它们的公共原点,这样就形成了一个平面直角坐标系.
x
y
o
30
20
10
20
10
-10
-20
-30
-40
-20
-50
-10
-70
-60
-50
-40
-30
-80
(-50,
北
西
30)
人民路
中山路
1
2
3
-1
-2
-3
O
1
-1
2
-2
-3
3
x
y
x轴
横轴
y轴
纵轴
直角坐标
系的原点
在平面内,两条互相垂直、原点重合的数轴,组成平面直角坐标系.
水平
位置
竖直
位置
x轴(横轴)
y轴(纵轴)
两坐标轴的交点为平面直角坐标系的原点
坐标轴
知识归纳
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A点在x 轴上的坐标为4
A点在y 轴上的坐标为2
A点在平面直角坐标系中的坐标为(4, 2)
记作:A(4,2)
X轴上的坐标
写在前面
·
B
B(-4,1)
知识归纳
平面直角坐标系中两条数轴特征:
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度一般取相同的
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
x
O
下面四个图形中,是平面直角坐标系的是( )
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
x
x
y
(A)
3 2 1 -1 -2 -3
x
y
(B)
2
1
-1
-2
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y
(D)
O
D
即学即练
平面上点的表示。
.
P
平面内任意一点P,过P点分别
向x、y轴作垂线,垂足在x轴、
y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
O
X
Y
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
在平面直角坐标系中
找点A(3,-2)
由坐标找点的方法:
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
A
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
例1.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
已知坐标平面内的点,说出它的坐标.
如图:说出A,B,C,D,M,N各点的坐标.
-4 –3 –2 –1 O
1 2 3 4 5
-1
-2
-3
-4
x
y
●
●
1
2
3
4
●
●
●
●
A
(3,4)
B
C
D
N
M
(-3,-4)
(0,2)
(0,-3)
(3,0)
(0,4)
即学即练
在平面直角坐标系中,两条坐标轴(即横轴和纵轴)把平面分成如图所示的Ⅰ,Ⅱ ,Ⅲ,Ⅳ四个区域.
分别称为第一,二,三,四象限.
注意:坐标轴上的点不属于任何一个象限.
目标导学二:直角坐标系中点的坐标的特征
探究各坐标轴上、象限内的点的特征.
(1)各坐标轴上的点的坐标有什么特征?
(2)各象限内的点的符号有什么特点?
合作探究
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
观察坐标系,填写各象限内的点的坐标的特征:
点的位置 横坐标的符号 纵坐标的
符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
交流:不看平面直角坐标系,你能迅速说出A(4,5) , B(-2,3), C(-4,
-1), D(2.5,-2), E(0,-4)所在的象限吗?你的方法又是什么?
合作探究
点的位置 横坐标的符号 纵坐标的
符号
在x轴的正半轴上
在x轴的负半轴上
在y轴的正半轴上
在y轴的负半轴上
0
+
+
-
-
0
0
0
交流:不看平面直角坐标系,你能迅速说出A(4,0),B(0,3),
C(-4,0),E(0,-4),O(0,0)所在的位置吗?你的方法又是什么?
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
E
活动2.观察坐标系,填写坐标轴上的点的坐标的特征:
特殊位置的点的符号特征:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
问题.坐标平面内的点与有序数对(坐标)是什么关系
类似数轴上的点与实数是一一对应的.我们可以得出:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
设点M(a,b)为平面直角坐标系内的点.
(1)当a>0,b<0时,点M位于第几象限?
(2)当ab>0时,点M位于第几象限?
(3)当a为任意有理数,且b<0时,点M位于第几象限?
解:(1)点M在第四象限;
(2)在第一象限(a>0,b>0)或者在第三象限(a<0,b<0);
(3)在第三象限(a<0,b<0)或者第四象限(a>0,b<0)或y轴负半轴上(a=0,b<0).
例2
例3:长方形的两条边长分别为4,6,建立适当的直角坐标系,使它的一个顶点的坐标为(-2,-3).请你写出另外三个顶点的坐标.
解:如图, 建立直角坐标系,
∵长方形的一个顶点的坐标为A(-2,-3),
∴长方形的另外三个顶点的坐标分别为B(2,-3),C(2,3),D(-2,3).
方法总结:由已知条件正确确定坐标轴的位置是解决本题的关键.
目标导学三:建立坐标系求图形中点的坐标
建立的平面直角坐标系不同,则各点的坐标也不同.你认为怎样建立直角坐标系才比较适当?
【总结】建立平面直角坐标系,一般要使图形上的点的坐标容易确定,例如以正方形的两条边所在的直线为坐标轴,建立平面直角坐标系,又如以正方形的中心为原点建立平面直角坐标系.需要说明的是,虽然建立不同的平面直角坐标系,同一个点会有不同的坐标,但正方形的形状和性质不会改变.
课堂小结
平面直角坐标系及点的坐标
定义:原点、坐标轴
点的坐标
定义与符号特征
点的坐标的确定
建立合适的平面直角坐标系
1.在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1)
C.(-3,-5) D.(3,-5)
D
检测目标
2.已知坐标平面内点A(m,n)在第四象限,那么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
B
检测目标
3.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在( )
A原点 Bx轴正半轴
C第一象限 D任意位置
B
检测目标
4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
(A)平行于x轴
(B)平行于y轴
(C)经过原点
(D)以上都不对
B
检测目标
5.如果在y轴上,那么点P的坐标是( )
A. B.
C. D.
【答案】B
【详解】
解:∵在y轴上,
∴解得,
∴点P的坐标是(0,-2).故选B.
检测目标
说说这节课你学到了什么
有什么体会
有什么感想
收获园地
作 业 :
1.完成同步练习题
2.背诵知识点
