2.2简谐运动的描述(29张PPT)
文档属性
| 名称 | 2.2简谐运动的描述(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 926.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-12 11:10:16 | ||
图片预览










文档简介
(共36张PPT)
第二章 机械运动
2.2 简谐运动的描述
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
1.知道简谐运动的振幅、周期和频率,知道全振动的含义.
2.知道周期和频率的关系. (重点)
3.理解简谐运动的方程,会根据提供的条件写出简谐运动位移与时间的关系式. (重点)
学习目标
问题:
有些物体的振动可以近似为简谐运动,做简谐运动的物体在一个位置附近不断地重复同样的运动。如何描述简谐运动的这种独特性呢?
?
新课导入
掌握简谐运动周期、频率的物理意义。
我们已经知道,做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系,因此,位移x的一般函数表达式可写为 x=Asin(ωt+φ)。
下面我们根据上述表达式,结合图所示情景,分析简谐运动的特点。
弹簧振子的简谐运动
(请点击小球)
O
A
A
掌握简谐运动周期、频率的物理意义。
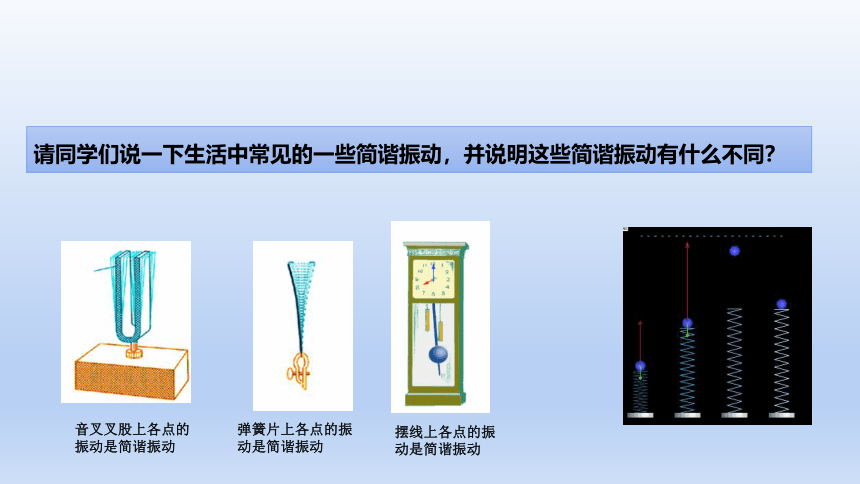
请同学们说一下生活中常见的一些简谐振动,并说明这些简谐振动有什么不同?
摆线上各点的振动是简谐振动
音叉叉股上各点的振动是简谐振动
弹簧片上各点的振动是简谐振动
描述简谐运动的物理量——振幅
一、 振幅
静止位置:即平衡位置
振子振动范围的大小,就是振幅的两倍2A。
意义:振幅是描述振动强弱的物理量,常用字母A表示。
位移:表示振动质点某时刻离开平衡位置的大小与方向。
定义:振动物体离开平衡位置的最大距离,叫做振动的振幅,单位是m。
新课讲解
描述简谐运动的物理量——振幅
一、 振幅
如图,在竖直弹簧振子的简谐运动中,O点为平衡位置,小球运动的最高点和最低点分别是M点和M’点,其振幅为:A=XOM。
描述简谐运动的物理量——振幅
一、 振幅
①振子的位移是偏离平衡位置的距离,故时刻在变化;但振幅是不变的。
②位移是矢量,振幅是标量,它等于最大位移的数值。
区分振幅和位移
对于一个给定的振动:
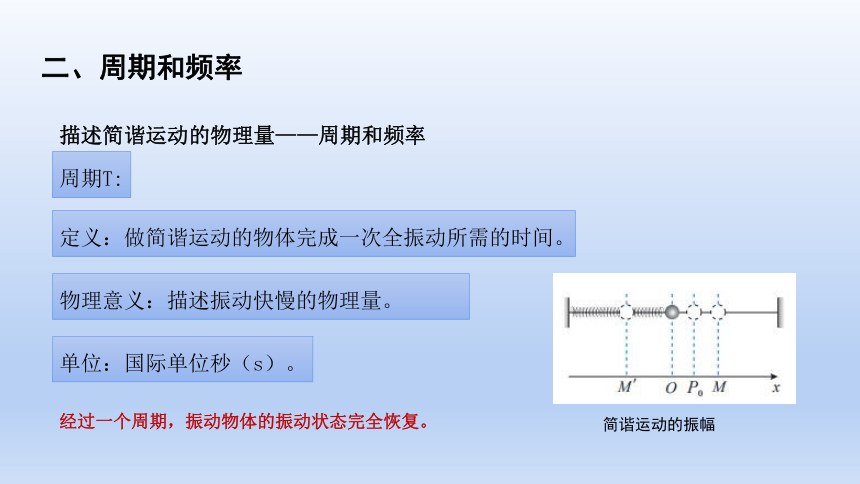
二、周期和频率
经过一个周期,振动物体的振动状态完全恢复。
描述简谐运动的物理量——周期和频率
周期T:做简谐运动的物体完成一次全振动所需的时间。
单位:s。
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
频率f:单位时间内完成的全振动的次数,单位:Hz。
二、周期和频率
定义:做简谐运动的物体完成一次全振动所需的时间。
描述简谐运动的物理量——周期和频率
周期T:
物理意义:描述振动快慢的物理量。
简谐运动的振幅
单位:国际单位秒(s)。
经过一个周期,振动物体的振动状态完全恢复。
二、周期和频率
定义:单位时间内完成全振动的次数,单位:Hz。
描述简谐运动的物理量——周期和频率
频率 f:
物理意义:描述振动快慢的物理量。
周期和频率之间的关系:
周期越小,频率越大,运动越快。
二、周期和频率
O
A
B
C
D
(请点击小球)
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
简谐运动的周期公式:
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关。
二、周期和频率
做一做
测量小球振动的周期
如图弹簧上端固定,下端悬挂钢球。把钢球从平衡位置向下拉一段距离 A,放手让其运动,A 就是振动的振幅。用停表测出钢球完成 n 个全振动所用的时间 t,nt 就是振动的周期。n 的值取大一些可以减小测量误差。再把振幅减小为原来的一半,用同样的方法测量振动的周期。
测量小球振动的周期
影响简谐运动周期大小的因素
二、周期和频率
(1)弹簧振子:弹簧振子是指小球和弹簧所组成的系统,是一种理想化模型。
(2)振子模型:常见的有水平弹簧振子和竖直弹簧振子。如图所示,图中球与杆之间的摩擦力及空气阻力可以忽略,且弹簧的质量与小球的质量相比可以忽略。
弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
三、相位
描述简谐运动的物理量——相位
描述周期性运动的物体在各个时刻所处状态的物理量。
以x代表质点对于平衡位置的位移,t代表时间,则:
三、相位
简谐运动的表达式
振幅
圆频率
初相位
相位
三、相位
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同。
反相:频率相同、相差为 的两个振子振动步伐调完全相反。
实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差。
三、相位
如果两个简谐运动的频率相同,其初相分别是
它们的相位差是
(1)取值范围: -π π
(2) ,表明两振动步调完全相同,称为同相。
π ,表明两振动步调完全相反,称为反相。
三、相位
(3) ,表示振动2比振动1超前。
,表示振动2比振动1滞后。
做一做:
观察两个小球的振动情况
并列悬挂两个相同的弹簧振子(图)。把小球向下拉同样的距离后同时放开,观察两球的振幅、周期、振动的步调。再次把两个小球拉到相同的位置,先把第一个小球放开,再放开第二个,观察两球的振幅、周期、振动的步调。
三、相位
观察两小球的振动
做一做:
用计算机呈现声音的振动图像
绝大多数计算机都有录音、放音的功能,并能在放音时显示声振动的图像。
用计算机的录音功能录制两个乐音,例如笛声,一个是 do,另一个是 sol,把它们保存起来。用媒体播放软件显示这个声音,把播放软件界面中“条形与波浪”的选项设为“波形”。这样可以从电脑屏幕上看到播放声音时的振动图像。按下“暂停”键得到静止的图像。
把 do 和 sol 这两个声音的振动图像复制到同一张空白幻灯片上,并把图像以外多余的区域裁掉,用计算机呈现声音的振动图像图比较两个声音的频率就得到图所示的图形。在屏幕上作出矩形框,调节框的宽度,使框内包含“do”的 10 个周期。在屏幕上观察,多少个“sol”的周期与“do”的 10 个周期的时间相等,由此可以得到“sol”和“do”的频率之比。如果已知其中一个声音的频率,还可以推知另一个声音的频率。请你想办法完成上面的操作。
三、相位
做一做:
用计算机呈现声音的振动图像
三、相位
比较两个声音的频率
乐音和音阶
科学漫步
在音乐理论中,把一组音按音调高低的次序排列起来就成为音阶,也就是大家都知道的do,re,mi,fa,sol,la,si,do(高)。下表列出了某乐律C调音阶中各音的频率。
乐音和音阶
科学漫步
有趣的是,高音do的频率正好是中音do的2倍,而且音阶中各音的频率与do的频率之比都是整数之比。
还有更有趣的事情。喜欢音乐的同学都知道,有些音一起演奏时听起来好听,有些音一起演奏时听起来不好听,前者叫作谐和音,后者叫作不谐和音。著名的大三和弦do、mi、sol的频率比是4:5:6,而小三和弦re、fa、la的频率比是10:12:15。大三和弦听起来更为和谐,那是因为三个音的频率比是更小的整数之比。随便拼凑在一起的三个音听起来不和谐,有兴趣的同学可以算一算它们的频率比,一定是三个比较大的整数。
乐音和音阶
科学漫步
从这个例子可以看到艺术后面的科学道理,但是,艺术远比“1+1=2”复杂。从上表中看出,频率增加一倍,音程高出8度。实际上这只对于中等音高是正确的。人的感觉十分复杂,对于高音段来说,频率要增加一倍多,听起来音高才高出一个8度。如果一个调音师按照“频率翻倍”的办法调钢琴,那就要出问题了。
尽管如此,科学家们还是可以通过音乐家的实际测听,确定音高与频率的对应关系,并且据此设计出优美动听的电子乐器。
例1、(单选)一质点做简谐运动的位移—时间图线如图所示.关于此质点的振动,下列说法中正确的是( )
A.质点做简谐运动的表达式为x=10sin(πt) cm
B.在0.5~1.0 s时间内,质点向x轴正向运动
C.在1.0~1.5 s时间内,质点的动能在增大
D.在1.0~1.5 s时间内,质点的加速度在增大
D
当堂小练
【答案】D
【解析】本题考查简谐振动.由图象可知,质点振幅为5 cm,振动周期T=2.0 s,则ω==π.因此,振动方程为x=5sin(πt)cm;0.5~1.0 s时间内,质点向x轴负向运动;1.0~1.5 s时间内,质点由平衡位置向x轴负向运动,速度逐渐减小,动能逐渐减小,加速度逐渐增大.选项ABC错误,D正确.
例2、(单选)如图,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。若小球从C点第一次运动到O点历时0.1 s,则小球振动的周期为 ( )
A.0.1 s B.0.2 s
C.0.3 s D.0.4 s
D
【答案】D
【解析】振子从C点第一次运动到O点的时间为0.1 s,对应的时间为一个周期的 ,故该弹簧振子的周期为0.4 s,D正确。
例3、(单选)如图所示,水平方向的弹簧振子振动过程中,振子先后经过a、b两点时的速度相同,且从a到b历时0.2 s,从b再回到a的最短时间为0.4 s,aO=bO,则该振子的振动频率为 ( )
A.1 Hz B.1.25 Hz C.2 Hz D.2.5 Hz
B
【答案】B
【解析】由题可知,a、b两点关于平衡位置对称,从a到b历时t1=0.2 s从b再回到a的最短时间为0.4 s,即从b到c所用时间为t2= s=0.1 s所以弹簧振子振动的周期为T=2t1+4t2=0.8 s则振动频率为f= =1.25 Hz,故B正确,A、C、D错误。
例4、(单选)某质点做简谐运动,其位移随时间变化的关系式为x=10sin cm,下列说法正确的是 ( )
A.该质点振动周期为T=4 s
B.该质点振幅A=10 cm
C.第1 s 末和第5 s 末质点的位移相同
D.2 s 内质点通过的路程一定为10 cm
B
【答案】B
【解析】根据x=10sin cm得:ω= rad/s,则该质点振动周期T= =8 s,则A错误。该质点振幅A=10 cm,则B正确。将t=1 s和t=5 s分别代入x=10sin cm得,位移分别为10sin cm和-10sin cm,则C错误。由于t=2 s= ,所以2 s内质点通过的路程可能小于一个振幅,也可能大于或等于一个振幅,则D错误。故选B。
THANKS
第二章 机械运动
2.2 简谐运动的描述
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
1.知道简谐运动的振幅、周期和频率,知道全振动的含义.
2.知道周期和频率的关系. (重点)
3.理解简谐运动的方程,会根据提供的条件写出简谐运动位移与时间的关系式. (重点)
学习目标
问题:
有些物体的振动可以近似为简谐运动,做简谐运动的物体在一个位置附近不断地重复同样的运动。如何描述简谐运动的这种独特性呢?
?
新课导入
掌握简谐运动周期、频率的物理意义。
我们已经知道,做简谐运动的物体的位移x与运动时间t之间满足正弦函数关系,因此,位移x的一般函数表达式可写为 x=Asin(ωt+φ)。
下面我们根据上述表达式,结合图所示情景,分析简谐运动的特点。
弹簧振子的简谐运动
(请点击小球)
O
A
A
掌握简谐运动周期、频率的物理意义。
请同学们说一下生活中常见的一些简谐振动,并说明这些简谐振动有什么不同?
摆线上各点的振动是简谐振动
音叉叉股上各点的振动是简谐振动
弹簧片上各点的振动是简谐振动
描述简谐运动的物理量——振幅
一、 振幅
静止位置:即平衡位置
振子振动范围的大小,就是振幅的两倍2A。
意义:振幅是描述振动强弱的物理量,常用字母A表示。
位移:表示振动质点某时刻离开平衡位置的大小与方向。
定义:振动物体离开平衡位置的最大距离,叫做振动的振幅,单位是m。
新课讲解
描述简谐运动的物理量——振幅
一、 振幅
如图,在竖直弹簧振子的简谐运动中,O点为平衡位置,小球运动的最高点和最低点分别是M点和M’点,其振幅为:A=XOM。
描述简谐运动的物理量——振幅
一、 振幅
①振子的位移是偏离平衡位置的距离,故时刻在变化;但振幅是不变的。
②位移是矢量,振幅是标量,它等于最大位移的数值。
区分振幅和位移
对于一个给定的振动:
二、周期和频率
经过一个周期,振动物体的振动状态完全恢复。
描述简谐运动的物理量——周期和频率
周期T:做简谐运动的物体完成一次全振动所需的时间。
单位:s。
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
频率f:单位时间内完成的全振动的次数,单位:Hz。
二、周期和频率
定义:做简谐运动的物体完成一次全振动所需的时间。
描述简谐运动的物理量——周期和频率
周期T:
物理意义:描述振动快慢的物理量。
简谐运动的振幅
单位:国际单位秒(s)。
经过一个周期,振动物体的振动状态完全恢复。
二、周期和频率
定义:单位时间内完成全振动的次数,单位:Hz。
描述简谐运动的物理量——周期和频率
频率 f:
物理意义:描述振动快慢的物理量。
周期和频率之间的关系:
周期越小,频率越大,运动越快。
二、周期和频率
O
A
B
C
D
(请点击小球)
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
简谐运动的周期公式:
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关。
二、周期和频率
做一做
测量小球振动的周期
如图弹簧上端固定,下端悬挂钢球。把钢球从平衡位置向下拉一段距离 A,放手让其运动,A 就是振动的振幅。用停表测出钢球完成 n 个全振动所用的时间 t,nt 就是振动的周期。n 的值取大一些可以减小测量误差。再把振幅减小为原来的一半,用同样的方法测量振动的周期。
测量小球振动的周期
影响简谐运动周期大小的因素
二、周期和频率
(1)弹簧振子:弹簧振子是指小球和弹簧所组成的系统,是一种理想化模型。
(2)振子模型:常见的有水平弹簧振子和竖直弹簧振子。如图所示,图中球与杆之间的摩擦力及空气阻力可以忽略,且弹簧的质量与小球的质量相比可以忽略。
弹簧振子的周期由振动系统本身的质量和劲度系数决定,而与振幅无关,所以常把周期和频率叫做固有周期和固有频率。
三、相位
描述简谐运动的物理量——相位
描述周期性运动的物体在各个时刻所处状态的物理量。
以x代表质点对于平衡位置的位移,t代表时间,则:
三、相位
简谐运动的表达式
振幅
圆频率
初相位
相位
三、相位
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同。
反相:频率相同、相差为 的两个振子振动步伐调完全相反。
实际上经常用到的是两个相同频率的简谐运动的相位差,简称相差。
三、相位
如果两个简谐运动的频率相同,其初相分别是
它们的相位差是
(1)取值范围: -π π
(2) ,表明两振动步调完全相同,称为同相。
π ,表明两振动步调完全相反,称为反相。
三、相位
(3) ,表示振动2比振动1超前。
,表示振动2比振动1滞后。
做一做:
观察两个小球的振动情况
并列悬挂两个相同的弹簧振子(图)。把小球向下拉同样的距离后同时放开,观察两球的振幅、周期、振动的步调。再次把两个小球拉到相同的位置,先把第一个小球放开,再放开第二个,观察两球的振幅、周期、振动的步调。
三、相位
观察两小球的振动
做一做:
用计算机呈现声音的振动图像
绝大多数计算机都有录音、放音的功能,并能在放音时显示声振动的图像。
用计算机的录音功能录制两个乐音,例如笛声,一个是 do,另一个是 sol,把它们保存起来。用媒体播放软件显示这个声音,把播放软件界面中“条形与波浪”的选项设为“波形”。这样可以从电脑屏幕上看到播放声音时的振动图像。按下“暂停”键得到静止的图像。
把 do 和 sol 这两个声音的振动图像复制到同一张空白幻灯片上,并把图像以外多余的区域裁掉,用计算机呈现声音的振动图像图比较两个声音的频率就得到图所示的图形。在屏幕上作出矩形框,调节框的宽度,使框内包含“do”的 10 个周期。在屏幕上观察,多少个“sol”的周期与“do”的 10 个周期的时间相等,由此可以得到“sol”和“do”的频率之比。如果已知其中一个声音的频率,还可以推知另一个声音的频率。请你想办法完成上面的操作。
三、相位
做一做:
用计算机呈现声音的振动图像
三、相位
比较两个声音的频率
乐音和音阶
科学漫步
在音乐理论中,把一组音按音调高低的次序排列起来就成为音阶,也就是大家都知道的do,re,mi,fa,sol,la,si,do(高)。下表列出了某乐律C调音阶中各音的频率。
乐音和音阶
科学漫步
有趣的是,高音do的频率正好是中音do的2倍,而且音阶中各音的频率与do的频率之比都是整数之比。
还有更有趣的事情。喜欢音乐的同学都知道,有些音一起演奏时听起来好听,有些音一起演奏时听起来不好听,前者叫作谐和音,后者叫作不谐和音。著名的大三和弦do、mi、sol的频率比是4:5:6,而小三和弦re、fa、la的频率比是10:12:15。大三和弦听起来更为和谐,那是因为三个音的频率比是更小的整数之比。随便拼凑在一起的三个音听起来不和谐,有兴趣的同学可以算一算它们的频率比,一定是三个比较大的整数。
乐音和音阶
科学漫步
从这个例子可以看到艺术后面的科学道理,但是,艺术远比“1+1=2”复杂。从上表中看出,频率增加一倍,音程高出8度。实际上这只对于中等音高是正确的。人的感觉十分复杂,对于高音段来说,频率要增加一倍多,听起来音高才高出一个8度。如果一个调音师按照“频率翻倍”的办法调钢琴,那就要出问题了。
尽管如此,科学家们还是可以通过音乐家的实际测听,确定音高与频率的对应关系,并且据此设计出优美动听的电子乐器。
例1、(单选)一质点做简谐运动的位移—时间图线如图所示.关于此质点的振动,下列说法中正确的是( )
A.质点做简谐运动的表达式为x=10sin(πt) cm
B.在0.5~1.0 s时间内,质点向x轴正向运动
C.在1.0~1.5 s时间内,质点的动能在增大
D.在1.0~1.5 s时间内,质点的加速度在增大
D
当堂小练
【答案】D
【解析】本题考查简谐振动.由图象可知,质点振幅为5 cm,振动周期T=2.0 s,则ω==π.因此,振动方程为x=5sin(πt)cm;0.5~1.0 s时间内,质点向x轴负向运动;1.0~1.5 s时间内,质点由平衡位置向x轴负向运动,速度逐渐减小,动能逐渐减小,加速度逐渐增大.选项ABC错误,D正确.
例2、(单选)如图,O点为弹簧振子的平衡位置,小球在B、C间做无摩擦的往复运动。若小球从C点第一次运动到O点历时0.1 s,则小球振动的周期为 ( )
A.0.1 s B.0.2 s
C.0.3 s D.0.4 s
D
【答案】D
【解析】振子从C点第一次运动到O点的时间为0.1 s,对应的时间为一个周期的 ,故该弹簧振子的周期为0.4 s,D正确。
例3、(单选)如图所示,水平方向的弹簧振子振动过程中,振子先后经过a、b两点时的速度相同,且从a到b历时0.2 s,从b再回到a的最短时间为0.4 s,aO=bO,则该振子的振动频率为 ( )
A.1 Hz B.1.25 Hz C.2 Hz D.2.5 Hz
B
【答案】B
【解析】由题可知,a、b两点关于平衡位置对称,从a到b历时t1=0.2 s从b再回到a的最短时间为0.4 s,即从b到c所用时间为t2= s=0.1 s所以弹簧振子振动的周期为T=2t1+4t2=0.8 s则振动频率为f= =1.25 Hz,故B正确,A、C、D错误。
例4、(单选)某质点做简谐运动,其位移随时间变化的关系式为x=10sin cm,下列说法正确的是 ( )
A.该质点振动周期为T=4 s
B.该质点振幅A=10 cm
C.第1 s 末和第5 s 末质点的位移相同
D.2 s 内质点通过的路程一定为10 cm
B
【答案】B
【解析】根据x=10sin cm得:ω= rad/s,则该质点振动周期T= =8 s,则A错误。该质点振幅A=10 cm,则B正确。将t=1 s和t=5 s分别代入x=10sin cm得,位移分别为10sin cm和-10sin cm,则C错误。由于t=2 s= ,所以2 s内质点通过的路程可能小于一个振幅,也可能大于或等于一个振幅,则D错误。故选B。
THANKS
