2021-2022学年青岛版八年级数学下册第7章实数 单元练习(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版八年级数学下册第7章实数 单元练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 334.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-11 08:12:48 | ||
图片预览




文档简介
第7章 实数测试卷
一、选择题
1.下列各数没有算术平方根的是 ( )
A.0 B.16 C.-4 D.2
2.在下列四组数中,不是勾股数的一组是 ( )
A.15,8,7 B.4,5,6 C.24,25,7 D.5,12,13
3.在实数,,,中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
4.16的平方根为 ( )
A.4 B.-4 C. D.
5.下列各式中正确的是 ( )
A. B. C. D.
6.下列说法正确的是 ( )
A.不存在最小的实数 B.有理数是有限小数
C.无限小数都是无理数 D.带根号的数都是无理数
7.实数3的相反数是 ( )
A. B. C. D.3
8.估计的值在 ( )
A.2到3之间 B.3到4之间
C.4到5之间 D.5到6之间
二、填空题
9.一个正方形的面积为5,则它的边长为_____.
10.若,则__.
11.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为________.
12.直角三角形的一直角边长4cm,斜边长5cm,则其斜边上的高是__________cm.
13.已知a,b,c为三角形的三边,若有(a+c)2=b2+2ac,则这个三角形的形状是_____三角形.
14.如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
15.如图,长方形的边落在数轴上,A、B两点在数轴上对应的数分别为和1,,连接,以B为圆心,为半径画弧交数轴于点E,则点E在数轴上所表示的数为_________.
16.数轴上A,B两点表示的数分别为﹣2和,点B关于点A的对称点为C,则点C所表示的数为___.
三、解答题
17.计算:.
18.解方程,求x的值.
(1)
(2)
19.已知一个数的算术平方根是m+4,平方根是±(3m+2),求这个数.
20.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
21.洋洋想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多米,当他把绳子的下端拉开米后,发现下端刚好接触地面,求旗杆的高度.
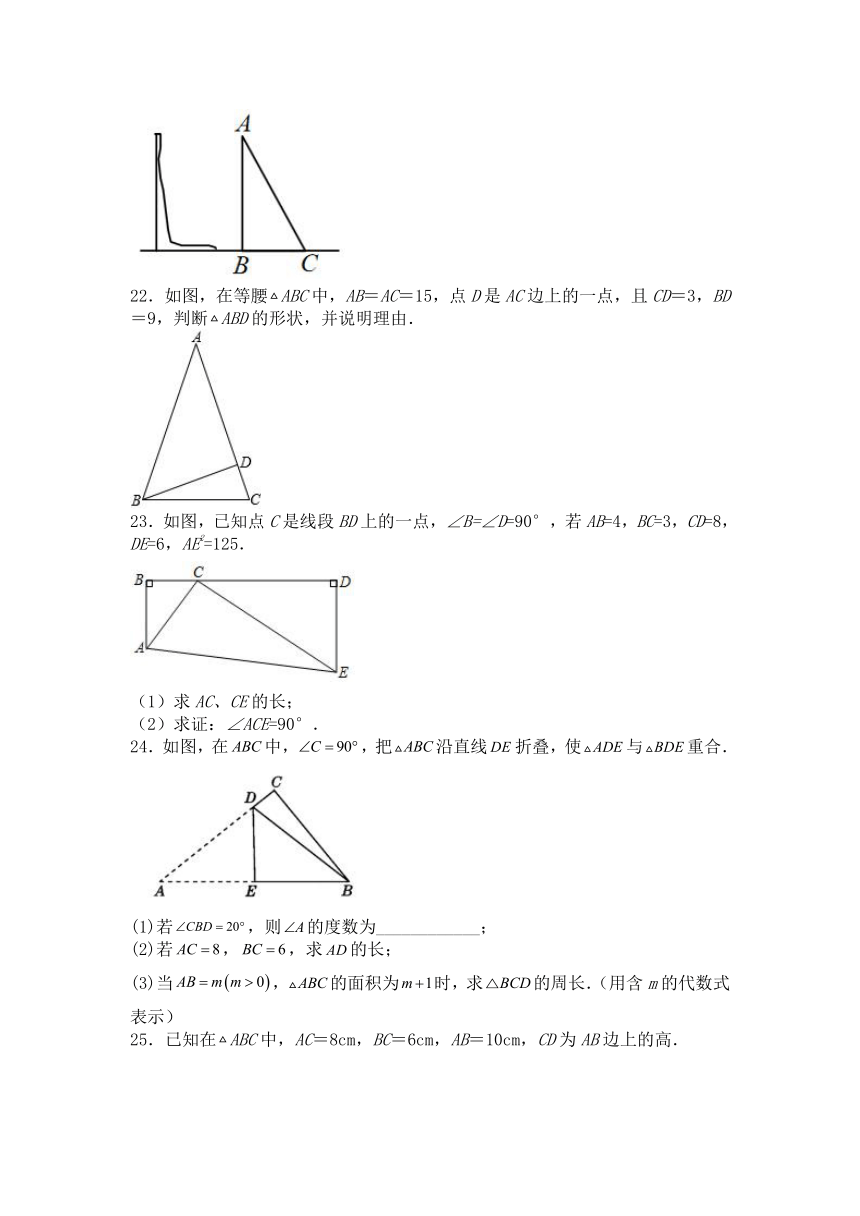
22.如图,在等腰ABC中,AB=AC=15,点D是AC边上的一点,且CD=3,BD=9,判断ABD的形状,并说明理由.
23.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=4,BC=3,CD=8,DE=6,AE2=125.
(1)求AC、CE的长;
(2)求证:∠ACE=90°.
24.如图,在中,,把沿直线折叠,使与重合.
(1)若,则的度数为____________;
(2)若,,求的长;
(3)当,的面积为时,求的周长.(用含m的代数式表示)
25.已知在ABC中,AC=8cm,BC=6cm,AB=10cm,CD为AB边上的高.
(1)判断ABC的形状,并说明理由.
(2)求CD的长;
(3)若动点P从点A出发,沿着A→C→B→A运动,最后回到A点,速度为1cm/s,设运动时间为ts.t为何值时,BCP为等腰三角形?
试卷第页,共页
参考答案:
1.C 2.B
【解析】
解:A、,故A不符合题意.
B、,故B符合题意.
C、,故C不符合题意.
D、,故D不符合题意.
故选:B.
3.B
【解析】
解:无理数是无限不循环小数,由定义知:,是无理数.
故选B.
4.D
【解析】
解:∵(±4)2=16,
∴16的平方根为±4,
故选:D.
5.D
【解析】
解:故A不符合题意;
故B不符合题意;
没有意义,故C不符合题意;
,运算正确,故D符合题意;
故选D
6.A
【解析】
略
7.C
【解析】
解:实数3的相反数是
故选C
8.A
【解析】
解:∵,
∴在4到5之间,
∴在2到3之间,
故选:A.
9.
【解析】
解:边长为:
故答案为
10.16
【解析】
解:由题意得,,,
解得,,
所以,.
故答案为:16.
11.25
【解析】
解:如图,,
,
则所代表的正方形的面积为25,
故答案为:25.
12.2.4
【解析】
解:设斜边上的高为hcm,
由勾股定理得,直角三角形另一条一直角边为:3,
由三角形的面积公式可得,
×3×4=×h×5,
解得,h=,
故答案为:.
13.直角
【解析】
解:∵(a+c)2=b2+2ac,
∴ ,
即,
所以该三角形是直角三角形.
故答案为:直角.
14.
【解析】
解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
15.
【解析】
解:四边形是长方形,A、B两点在数轴上对应的数分别为和1,,
依题意.
设点E在数轴上所表示的数为,则
解得
故答案为:
16.
【解析】
解:∵点B关于点A的对称点为C,
∴CA=AB=|-(-2)|=+2,
设点C所表示的数是x,
∴CA=|-2-x|=+2,
∴x=-2±(+2)=-4±,
∵C点在原点左侧,
∴C表示的数:-4-,
故答案为:.
17.2
【解析】
解:
18.(1)或 ;(2)x=
【解析】
解:(1),
,
或 ;
(2)8(x 1)3= 27,
(x 1)3= ,
x 1= ,
x= .
19.25或
【解析】
解:(1)当m+4=3m+2时,m=1,m+4=5,所以这个数为25;
(2)当m+4=-3m-2时,m=,m+4=,所以这个数为.
这个数是25或
20.【解析】
(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
21.米
【解析】
解:设旗杆的高度为x米,则绳子的长度为(x+2)米,
根据勾股定理可得:x2+52=(x+2)2,
解得,x=.
答:旗杆的高度为米.
22.ABD是直角三角形,见解析
【解析】
△ABD是直角三角形,
理由是:∵AC=15,CD=3,
∴AD=AC﹣CD=15﹣3=12,
∵AB=15,BD=9,
∴BD2+AD2=AB2,
∴ABD是直角三角形.
23.(1);;(2)见解析.
【解析】
(1)解:∵在中,
∴
∵在中,
∴
(2)证明:∵,,,
∴,
∴为直角三角形,
24.(1);
(2)的长为;
(3)的周长为:
【解析】
(1)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴∠ABD=∠A,
∵∠C=90°,∠CBD=20°,
∴∠ABD+∠A=180°-90°-20°=70°,
∴∠A=70°÷2=35°,
故答案为:35°;
(2)
∵与重合,
∴,
∴设,则,
在中,由勾股定理可得:,
∴,
解得:,
∴的长为;
(3)
∵,的面积为,
∴,
∴,
在中,,
由勾股定理可得:,
∴,
∴,
∴,
∵,
∴的周长为:.
25.(1)直角三角形,证明见解析;(2)cm;(3)2或20或19或
【解析】
解:(1)△ABC是直角三角形,
理由:∵AC=8cm,BC=6cm,AB=10cm,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△ABC是直角三角形.
(2)∵CD⊥AB,△ABC是直角三角形,
∴S△ABC= CD AB= AC BC,
∴×CD×10=×8×6,
∴CD=cm;
(3)∵∠C=90°,AB=10cm,BC=6cm,AC=8cm,
△BCP为等腰三角形时,分三种情况:
①如果CP=CB,那么点P在AC上,AP=2cm,此时t=2(秒);
②如果BC=BP,那么点P在AB上,BP=6cm,CA+BC+BP=8+6+6=20(cm),此时t=20(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+BC+BP=8+6+5=19(cm),t=19(秒),
④当CP=CB时,t=8+6+2×=,
综上可知,当t=2或20或19或时,△BCP为等腰三角形.
试卷第页,共页
试卷第7页,共7页
一、选择题
1.下列各数没有算术平方根的是 ( )
A.0 B.16 C.-4 D.2
2.在下列四组数中,不是勾股数的一组是 ( )
A.15,8,7 B.4,5,6 C.24,25,7 D.5,12,13
3.在实数,,,中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
4.16的平方根为 ( )
A.4 B.-4 C. D.
5.下列各式中正确的是 ( )
A. B. C. D.
6.下列说法正确的是 ( )
A.不存在最小的实数 B.有理数是有限小数
C.无限小数都是无理数 D.带根号的数都是无理数
7.实数3的相反数是 ( )
A. B. C. D.3
8.估计的值在 ( )
A.2到3之间 B.3到4之间
C.4到5之间 D.5到6之间
二、填空题
9.一个正方形的面积为5,则它的边长为_____.
10.若,则__.
11.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为________.
12.直角三角形的一直角边长4cm,斜边长5cm,则其斜边上的高是__________cm.
13.已知a,b,c为三角形的三边,若有(a+c)2=b2+2ac,则这个三角形的形状是_____三角形.
14.如图,点D在△ABC内,∠BDC=90°,AB=3,AC=BD=2,CD=1,则图中阴影部分的面积为 _______________.
15.如图,长方形的边落在数轴上,A、B两点在数轴上对应的数分别为和1,,连接,以B为圆心,为半径画弧交数轴于点E,则点E在数轴上所表示的数为_________.
16.数轴上A,B两点表示的数分别为﹣2和,点B关于点A的对称点为C,则点C所表示的数为___.
三、解答题
17.计算:.
18.解方程,求x的值.
(1)
(2)
19.已知一个数的算术平方根是m+4,平方根是±(3m+2),求这个数.
20.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个等腰三角形(不含直角),使它的面积为8;
(2)在图2中,画一个直角三角形,使它的三边长都是有理数;
(3)在图3中,画一个正方形,使它的面积为10.
21.洋洋想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多米,当他把绳子的下端拉开米后,发现下端刚好接触地面,求旗杆的高度.
22.如图,在等腰ABC中,AB=AC=15,点D是AC边上的一点,且CD=3,BD=9,判断ABD的形状,并说明理由.
23.如图,已知点C是线段BD上的一点,∠B=∠D=90°,若AB=4,BC=3,CD=8,DE=6,AE2=125.
(1)求AC、CE的长;
(2)求证:∠ACE=90°.
24.如图,在中,,把沿直线折叠,使与重合.
(1)若,则的度数为____________;
(2)若,,求的长;
(3)当,的面积为时,求的周长.(用含m的代数式表示)
25.已知在ABC中,AC=8cm,BC=6cm,AB=10cm,CD为AB边上的高.
(1)判断ABC的形状,并说明理由.
(2)求CD的长;
(3)若动点P从点A出发,沿着A→C→B→A运动,最后回到A点,速度为1cm/s,设运动时间为ts.t为何值时,BCP为等腰三角形?
试卷第页,共页
参考答案:
1.C 2.B
【解析】
解:A、,故A不符合题意.
B、,故B符合题意.
C、,故C不符合题意.
D、,故D不符合题意.
故选:B.
3.B
【解析】
解:无理数是无限不循环小数,由定义知:,是无理数.
故选B.
4.D
【解析】
解:∵(±4)2=16,
∴16的平方根为±4,
故选:D.
5.D
【解析】
解:故A不符合题意;
故B不符合题意;
没有意义,故C不符合题意;
,运算正确,故D符合题意;
故选D
6.A
【解析】
略
7.C
【解析】
解:实数3的相反数是
故选C
8.A
【解析】
解:∵,
∴在4到5之间,
∴在2到3之间,
故选:A.
9.
【解析】
解:边长为:
故答案为
10.16
【解析】
解:由题意得,,,
解得,,
所以,.
故答案为:16.
11.25
【解析】
解:如图,,
,
则所代表的正方形的面积为25,
故答案为:25.
12.2.4
【解析】
解:设斜边上的高为hcm,
由勾股定理得,直角三角形另一条一直角边为:3,
由三角形的面积公式可得,
×3×4=×h×5,
解得,h=,
故答案为:.
13.直角
【解析】
解:∵(a+c)2=b2+2ac,
∴ ,
即,
所以该三角形是直角三角形.
故答案为:直角.
14.
【解析】
解:,,,
,
,,
,
是直角三角形,,
阴影,
故答案为:.
15.
【解析】
解:四边形是长方形,A、B两点在数轴上对应的数分别为和1,,
依题意.
设点E在数轴上所表示的数为,则
解得
故答案为:
16.
【解析】
解:∵点B关于点A的对称点为C,
∴CA=AB=|-(-2)|=+2,
设点C所表示的数是x,
∴CA=|-2-x|=+2,
∴x=-2±(+2)=-4±,
∵C点在原点左侧,
∴C表示的数:-4-,
故答案为:.
17.2
【解析】
解:
18.(1)或 ;(2)x=
【解析】
解:(1),
,
或 ;
(2)8(x 1)3= 27,
(x 1)3= ,
x 1= ,
x= .
19.25或
【解析】
解:(1)当m+4=3m+2时,m=1,m+4=5,所以这个数为25;
(2)当m+4=-3m-2时,m=,m+4=,所以这个数为.
这个数是25或
20.【解析】
(1)如图所示,三角形底为4,高为4,面积为8,符合题意,即为所求;
(2)如图所示,三角形为所求,直角边分别为3,4,根据勾股定理,斜边为5,符合题意;
(3)如图所示,正方形为所求,正方形变长为,
面积为:,符合题意.
21.米
【解析】
解:设旗杆的高度为x米,则绳子的长度为(x+2)米,
根据勾股定理可得:x2+52=(x+2)2,
解得,x=.
答:旗杆的高度为米.
22.ABD是直角三角形,见解析
【解析】
△ABD是直角三角形,
理由是:∵AC=15,CD=3,
∴AD=AC﹣CD=15﹣3=12,
∵AB=15,BD=9,
∴BD2+AD2=AB2,
∴ABD是直角三角形.
23.(1);;(2)见解析.
【解析】
(1)解:∵在中,
∴
∵在中,
∴
(2)证明:∵,,,
∴,
∴为直角三角形,
24.(1);
(2)的长为;
(3)的周长为:
【解析】
(1)∵把△ABC沿直线DE折叠,使△ADE与△BDE重合,
∴∠ABD=∠A,
∵∠C=90°,∠CBD=20°,
∴∠ABD+∠A=180°-90°-20°=70°,
∴∠A=70°÷2=35°,
故答案为:35°;
(2)
∵与重合,
∴,
∴设,则,
在中,由勾股定理可得:,
∴,
解得:,
∴的长为;
(3)
∵,的面积为,
∴,
∴,
在中,,
由勾股定理可得:,
∴,
∴,
∴,
∵,
∴的周长为:.
25.(1)直角三角形,证明见解析;(2)cm;(3)2或20或19或
【解析】
解:(1)△ABC是直角三角形,
理由:∵AC=8cm,BC=6cm,AB=10cm,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴△ABC是直角三角形.
(2)∵CD⊥AB,△ABC是直角三角形,
∴S△ABC= CD AB= AC BC,
∴×CD×10=×8×6,
∴CD=cm;
(3)∵∠C=90°,AB=10cm,BC=6cm,AC=8cm,
△BCP为等腰三角形时,分三种情况:
①如果CP=CB,那么点P在AC上,AP=2cm,此时t=2(秒);
②如果BC=BP,那么点P在AB上,BP=6cm,CA+BC+BP=8+6+6=20(cm),此时t=20(秒);
③如果PB=PC,那么点P在BC的垂直平分线与AB的交点处,即在AB的中点,此时CA+BC+BP=8+6+5=19(cm),t=19(秒),
④当CP=CB时,t=8+6+2×=,
综上可知,当t=2或20或19或时,△BCP为等腰三角形.
试卷第页,共页
试卷第7页,共7页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
